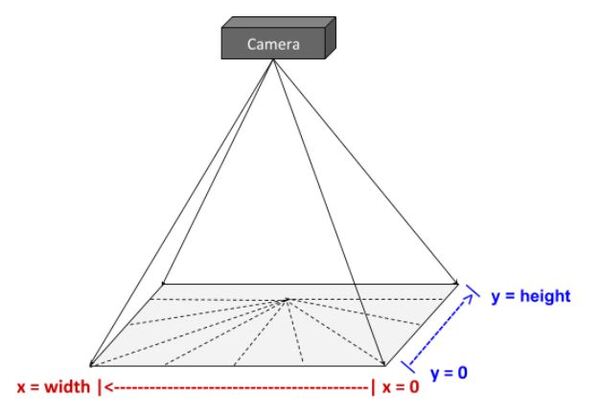
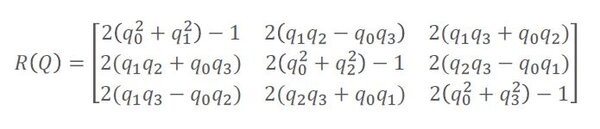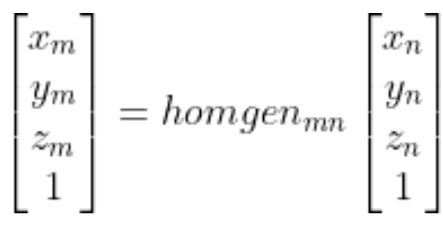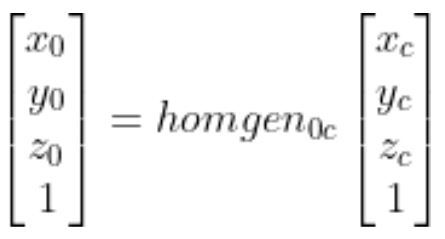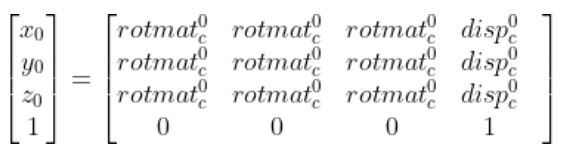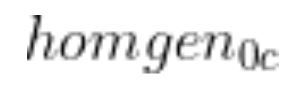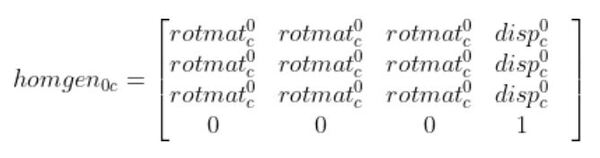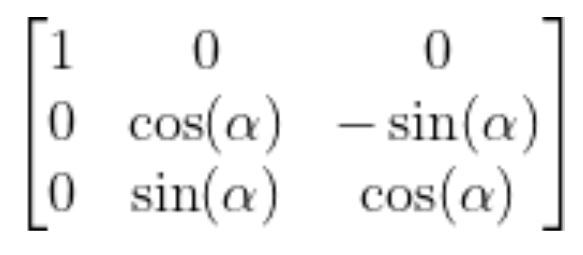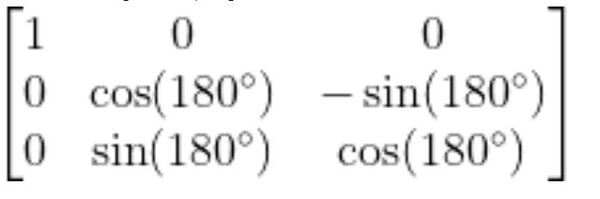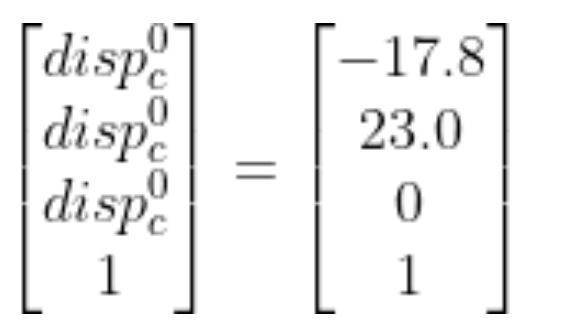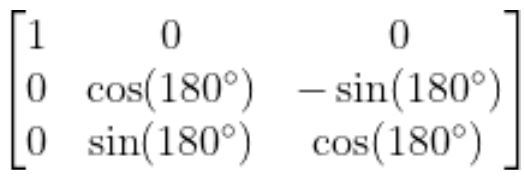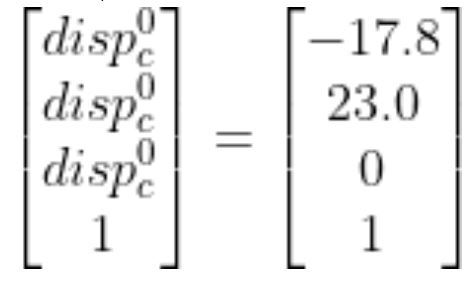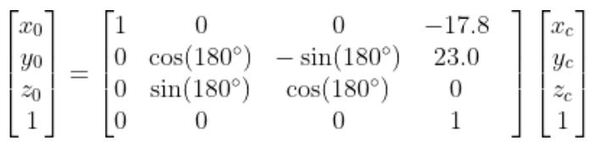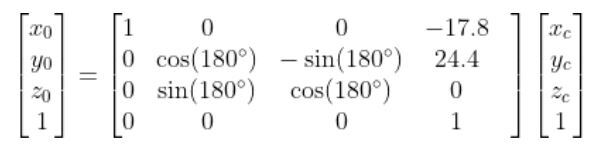In this tutorial, we’ll learn how to convert camera pixel coordinates to coordinates that are relative to the base frame for a robotic arm.

Prerequisites

This tutorial will make a lot more sense if you’ve gone through the following tutorials first. Otherwise, if you are already familiar with terms like “homogeneous transformation matrix,” jump right ahead into this tutorial.

• You completed this tutorial to build a two degree of freedom robotic arm.
• You know how to draw the kinematic diagram for a two degree of freedom robotic arm.
• You know how to draw Denavit-Hartenberg Frames for a two degree of freedom robotic arm.
• You understand what homogeneous transformation matrices are and how to write them in code.
• You know how to find rotation matrices between coordinate frames.
• You know how to find displacement vectors between coordinate frames.
• You know how to convert camera pixels to real-world (centimeter) coordinates.

Case 1: Camera Lens is Parallel to the Surface

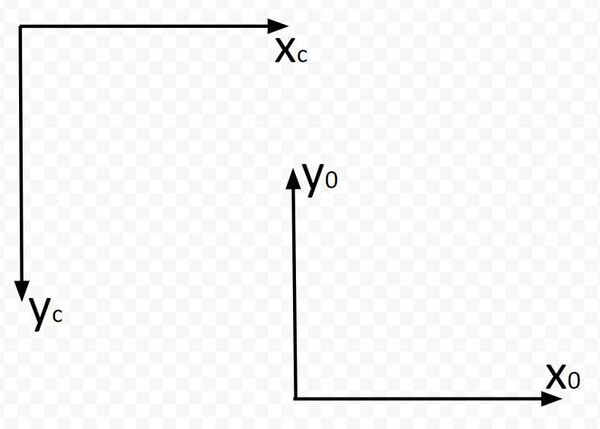
Label the Axes

Here is a two degree of freedom robotic arm that I built.

Here is the diagram of this robotic arm.

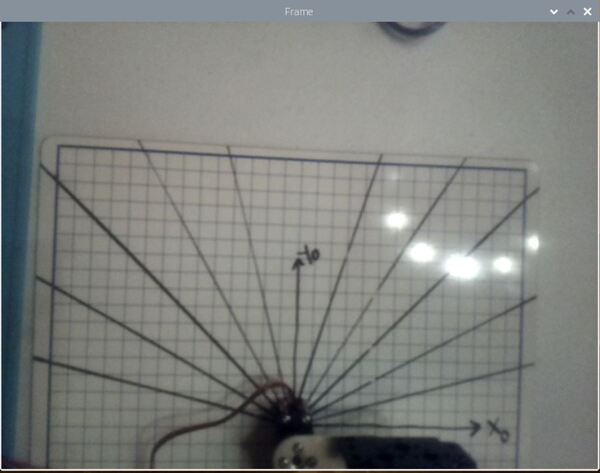
What we need to do is to draw the frames on the dry-erase board.

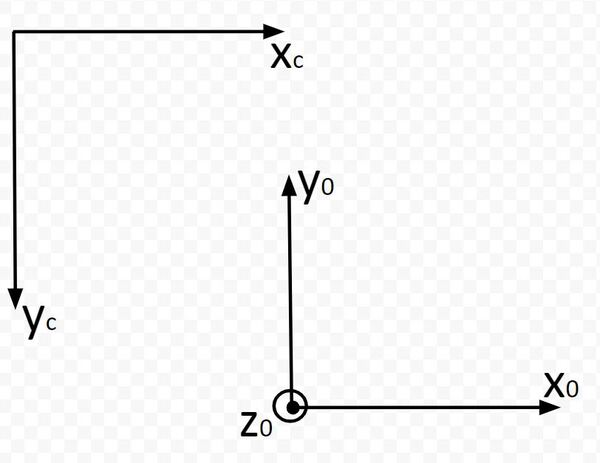
The origin of the base frame of the robotic arm is located here.

The x₀ axis is this line here.

The y₀ axis is this line here.

Open up your Raspberry Pi and turn on the video stream by running the following code:

# Credit: Adrian Rosebrock
# https://www.pyimagesearch.com/2015/03/30/accessing-the-raspberry-pi-camera-with-opencv-and-python/

# import the necessary packages
from picamera.array import PiRGBArray # Generates a 3D RGB array
from picamera import PiCamera # Provides a Python interface for the RPi Camera Module
import time # Provides time-related functions
import cv2 # OpenCV library

# Initialize the camera
camera = PiCamera()

# Set the camera resolution
camera.resolution = (640, 480)

# Set the number of frames per second
camera.framerate = 32

# Generates a 3D RGB array and stores it in rawCapture
raw_capture = PiRGBArray(camera, size=(640, 480))

# Wait a certain number of seconds to allow the camera time to warmup
time.sleep(0.1)

# Capture frames continuously from the camera
for frame in camera.capture_continuous(raw_capture, format="bgr", use_video_port=True):
    
    # Grab the raw NumPy array representing the image
    image = frame.array
    
    # Display the frame using OpenCV
    cv2.imshow("Frame", image)
    
    # Wait for keyPress for 1 millisecond
    key = cv2.waitKey(1) & 0xFF
    
    # Clear the stream in preparation for the next frame
    raw_capture.truncate(0)
    
    # If the `q` key was pressed, break from the loop
    if key == ord("q"):
        break

Let’s label the origin for the camera reference frame. The origin (x = 0, y = 0) for the camera reference frame is located in the far upper-left corner of the screen. I’ve put a screw driver head on the table to mark the location of the origin of the camera frame.

The x axis for the camera frame runs to the right from the origin along the top of the field of view. I’ll label this axis x_c.

The y axis for the camera frame runs downward from the origin along the left side of the field of view. I’ll label this axis y_c.

Press CTRL + C to stop the code from running.

Run the Object Detector Code

Run this code (absolute_difference_method_cm.py):

# Author: Addison Sears-Collins
# Description: This algorithm detects objects in a video stream
#   using the Absolute Difference Method. The idea behind this 
#   algorithm is that we first take a snapshot of the background.
#   We then identify changes by taking the absolute difference 
#   between the current video frame and that original 
#   snapshot of the background (i.e. first frame). 

# import the necessary packages
from picamera.array import PiRGBArray # Generates a 3D RGB array
from picamera import PiCamera # Provides a Python interface for the RPi Camera Module
import time # Provides time-related functions
import cv2 # OpenCV library
import numpy as np # Import NumPy library

# Initialize the camera
camera = PiCamera()

# Set the camera resolution
camera.resolution = (640, 480)

# Set the number of frames per second
camera.framerate = 30

# Generates a 3D RGB array and stores it in rawCapture
raw_capture = PiRGBArray(camera, size=(640, 480))

# Wait a certain number of seconds to allow the camera time to warmup
time.sleep(0.1)

# Initialize the first frame of the video stream
first_frame = None

# Create kernel for morphological operation. You can tweak
# the dimensions of the kernel.
# e.g. instead of 20, 20, you can try 30, 30
kernel = np.ones((20,20),np.uint8)

# Centimeter to pixel conversion factor
# I measured 32.0 cm across the width of the field of view of the camera.
CM_TO_PIXEL = 32.0 / 640

# Capture frames continuously from the camera
for frame in camera.capture_continuous(raw_capture, format="bgr", use_video_port=True):
    
    # Grab the raw NumPy array representing the image
    image = frame.array

    # Convert the image to grayscale
    gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    
    # Close gaps using closing
    gray = cv2.morphologyEx(gray,cv2.MORPH_CLOSE,kernel)
      
    # Remove salt and pepper noise with a median filter
    gray = cv2.medianBlur(gray,5)
    
    # If first frame, we need to initialize it.
    if first_frame is None:
        
      first_frame = gray
      
      # Clear the stream in preparation for the next frame
      raw_capture.truncate(0)
      
      # Go to top of for loop
      continue
      
    # Calculate the absolute difference between the current frame
    # and the first frame
    absolute_difference = cv2.absdiff(first_frame, gray)

    # If a pixel is less than ##, it is considered black (background). 
    # Otherwise, it is white (foreground). 255 is upper limit.
    # Modify the number after absolute_difference as you see fit.
    _, absolute_difference = cv2.threshold(absolute_difference, 50, 255, cv2.THRESH_BINARY)

    # Find the contours of the object inside the binary image
    contours, hierarchy = cv2.findContours(absolute_difference,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE)[-2:]
    areas = [cv2.contourArea(c) for c in contours]
 
    # If there are no countours
    if len(areas) < 1:
 
      # Display the resulting frame
      cv2.imshow('Frame',image)
 
      # Wait for keyPress for 1 millisecond
      key = cv2.waitKey(1) & 0xFF
 
      # Clear the stream in preparation for the next frame
      raw_capture.truncate(0)
    
      # If "q" is pressed on the keyboard, 
      # exit this loop
      if key == ord("q"):
        break
    
      # Go to the top of the for loop
      continue
 
    else:
        
      # Find the largest moving object in the image
      max_index = np.argmax(areas)
      
    # Draw the bounding box
    cnt = contours[max_index]
    x,y,w,h = cv2.boundingRect(cnt)
    cv2.rectangle(image,(x,y),(x+w,y+h),(0,255,0),3)
 
    # Draw circle in the center of the bounding box
    x2 = x + int(w/2)
    y2 = y + int(h/2)
    cv2.circle(image,(x2,y2),4,(0,255,0),-1)
	
    # Calculate the center of the bounding box in centimeter coordinates
    # instead of pixel coordinates
    x2_cm = x2 * CM_TO_PIXEL
    y2_cm = y2 * CM_TO_PIXEL
 
    # Print the centroid coordinates (we'll use the center of the
    # bounding box) on the image
    text = "x: " + str(x2_cm) + ", y: " + str(y2_cm)
    cv2.putText(image, text, (x2 - 10, y2 - 10),
      cv2.FONT_HERSHEY_SIMPLEX, 0.5, (0, 255, 0), 2)
         
    # Display the resulting frame
    cv2.imshow("Frame",image)
    
    # Wait for keyPress for 1 millisecond
    key = cv2.waitKey(1) & 0xFF
 
    # Clear the stream in preparation for the next frame
    raw_capture.truncate(0)
    
    # If "q" is pressed on the keyboard, 
    # exit this loop
    if key == ord("q"):
      break

# Close down windows
cv2.destroyAllWindows()

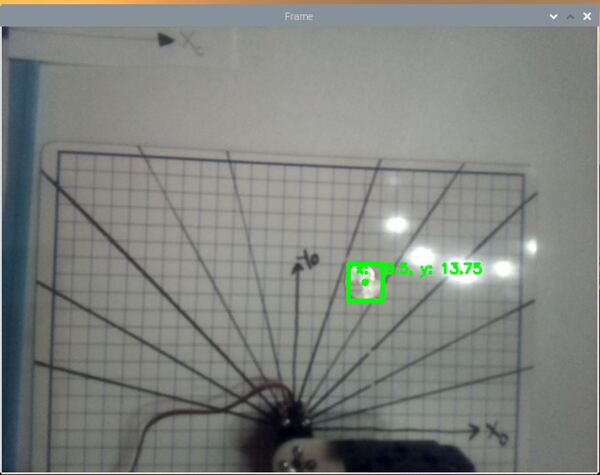
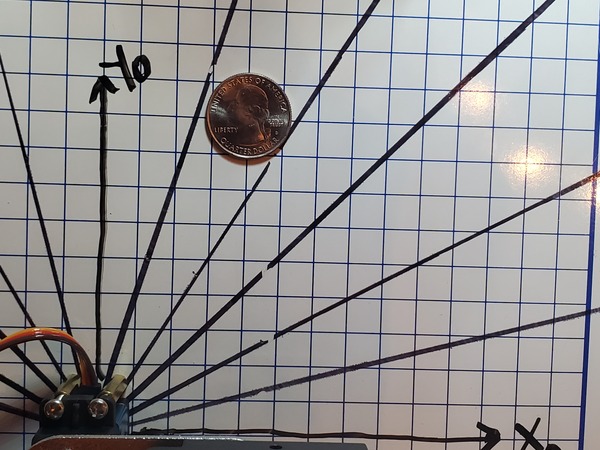
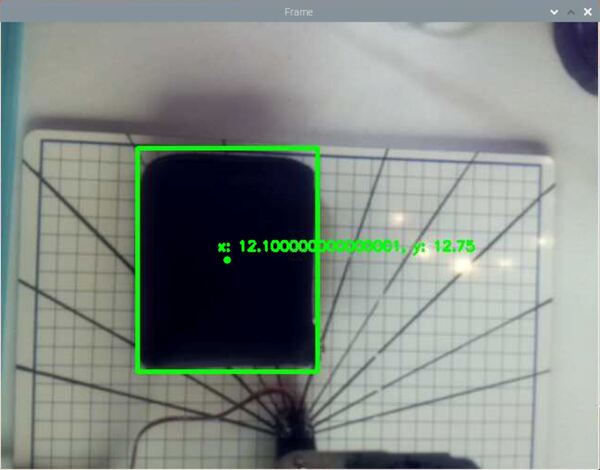
Now, grab an object. I’ll grab a quarter and place it in the field of view.

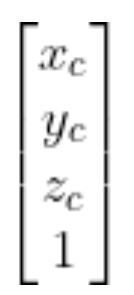
You can see the position of the quarter in the camera reference frame is:

• x_c in centimeters = 19.5 cm
• y_c in centimeters = 13.75 cm
• z_c in centimeters = 0.0 cm

Finding the Homogeneous Transformation Matrix

This is cool, but what I really want to know are the coordinates of the quarter relative to the base frame of my two degree of freedom robotic arm. 

If I know the coordinates of the object relative to the base frame of my two degree of freedom robotic arm, I can then use inverse kinematics to command the robot to move the end effector to that location.

A tool that can help us do that is known as the homogeneous transformation matrix.

A homogeneous transformation matrix is a 4×4 matrix (i.e. 4 rows and 4 columns) that enables us to find the position of a point in reference frame m (e.g. the robotic arm base frame) given the position of a point in reference frame n (e.g. the camera reference frame).

In other words:

More, specifically:

Which is the same thing as…

So you can see that if we know the vector:

If we can then determine the 4×4 matrix…

…and multiply the two terms together, We can calculate…

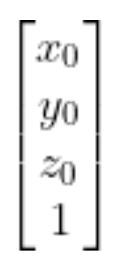
the position of the object in the robotic arm base reference frame.

homgen_0c has two pieces we need to find. We need to find the rotation matrix portion (i.e. the 3×3 matrix on the left. We also need to find the displacement vector portion (the rightmost column).

Calculate the Rotation Matrix That Converts the Camera Reference Frame to the Base Frame

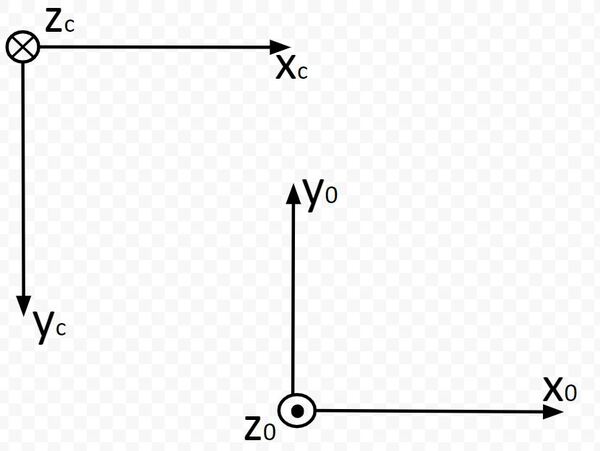
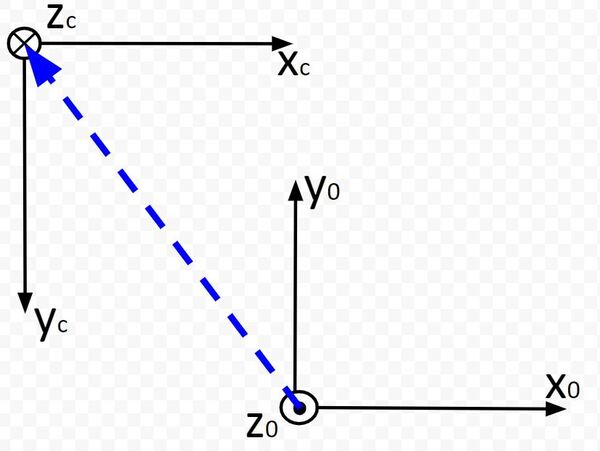
Let’s start by finding the rotation matrix portion. I’m going to draw the camera and robotic base reference frames below. We first need to look at how we can rotate the base frame to match up with the camera frame of the robotic arm.

Which way is z₀ pointing? Using the right hand rule, take your four fingers and point them towards the x₀ axis. Your palm faces towards y₀. Your thumb points towards z₀, which is upwards out of the page (or upwards out of the dry erase board). I’ll mark this with a dark circle.

Which way is z_c pointing? Using the right hand rule, take your four fingers and point them towards the x_c axis. Your palm faces towards y_c. Your thumb points towards z_c, which is downwards into the page (or downward into the dry erase board). I’m marking this with an X.

Now, stick your thumb in the direction of x₀. Your thumb points is the axis of rotation, while your four fingers indicate the direction of positive rotation. You can see that we would need to rotate frame 0 an angle of +180 degrees around the x₀ axis in order to get frame 0 to match up with frame c (the camera reference frame).

The standard rotation matrix for rotation around the x-axis is…

Substitute 180 degrees for ɑ, we get:

Calculate the Displacement Vector

Now that we have the rotation matrix portion of the homogeneous transformation matrix, we need to calculate the displacement vector from the origin of frame 0 to the origin of frame c.

Displacement Along x₀

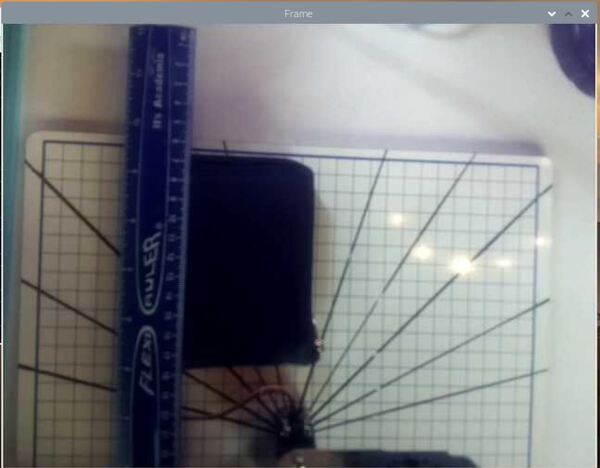
Grab your ruler and measure the distance from the origin of frame 0 to the origin of frame c along the x₀ axis. 

I measured -17.8 cm (because the displacement is in the negative x₀ direction).

Displacement Along y₀

Grab your ruler and measure the distance from the origin of frame 0 to the origin of frame c along the y₀ axis. 

I measured 23.0 cm.

Displacement Along z₀

Both reference frames are in the same z plane, so there is no displacement along z₀ from frame 0 to frame c.

Therefore, we have 0.0 cm.

The full displacement vector is:

Putting It All Together

Now that we have our rotation matrix…

and our displacement vector…

we put them both together to get the following homogeneous transformation matrix.

We can now convert a point in the camera reference frame to a point in the base frame of the robotic arm.

Print the Base Frame Coordinates of an Object

Now, let’s modify our absolute_difference_method_cm.py program so that we display an object’s x and y position in base frame coordinates rather than camera frame coordinates. I remeasured the width of the field of view in centimeters and calculated it as 36.0 cm.

I’ll name the program display_base_frame_coordinates.py.

Here is the code:

# Author: Addison Sears-Collins
# Description: This algorithm detects objects in a video stream
#   using the Absolute Difference Method. The idea behind this 
#   algorithm is that we first take a snapshot of the background.
#   We then identify changes by taking the absolute difference 
#   between the current video frame and that original 
#   snapshot of the background (i.e. first frame).
#   The coordinates of an object are displayed relative to
#   the base frame of a two degree of freedom robotic arm.

# import the necessary packages
from picamera.array import PiRGBArray # Generates a 3D RGB array
from picamera import PiCamera # Provides a Python interface for the RPi Camera Module
import time # Provides time-related functions
import cv2 # OpenCV library
import numpy as np # Import NumPy library

# Initialize the camera
camera = PiCamera()

# Set the camera resolution
camera.resolution = (640, 480)

# Set the number of frames per second
camera.framerate = 30

# Generates a 3D RGB array and stores it in rawCapture
raw_capture = PiRGBArray(camera, size=(640, 480))

# Wait a certain number of seconds to allow the camera time to warmup
time.sleep(0.1)

# Initialize the first frame of the video stream
first_frame = None

# Create kernel for morphological operation. You can tweak
# the dimensions of the kernel.
# e.g. instead of 20, 20, you can try 30, 30
kernel = np.ones((20,20),np.uint8)

# Centimeter to pixel conversion factor
# I measured 36.0 cm across the width of the field of view of the camera.
CM_TO_PIXEL = 36.0 / 640

# Define the rotation matrix from the robotic base frame (frame 0)
# to the camera frame (frame c).
rot_angle = 180 # angle between axes in degrees
rot_angle = np.deg2rad(rot_angle)
rot_mat_0_c = np.array([[1, 0, 0],
                        [0, np.cos(rot_angle), -np.sin(rot_angle)],
                        [0, np.sin(rot_angle), np.cos(rot_angle)]])

# Define the displacement vector from frame 0 to frame c
disp_vec_0_c = np.array([[-17.8],
                         [24.4], # This was originally 23.0 but I modified it for accuracy
                         [0.0]])

# Row vector for bottom of homogeneous transformation matrix
extra_row_homgen = np.array([[0, 0, 0, 1]])

# Create the homogeneous transformation matrix from frame 0 to frame c
homgen_0_c = np.concatenate((rot_mat_0_c, disp_vec_0_c), axis=1) # side by side
homgen_0_c = np.concatenate((homgen_0_c, extra_row_homgen), axis=0) # one above the other

# Initialize coordinates in the robotic base frame
coord_base_frame = np.array([[0.0],
                             [0.0],
                             [0.0],
                             [1]])

# Capture frames continuously from the camera
for frame in camera.capture_continuous(raw_capture, format="bgr", use_video_port=True):
    
    # Grab the raw NumPy array representing the image
    image = frame.array

    # Convert the image to grayscale
    gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    
    # Close gaps using closing
    gray = cv2.morphologyEx(gray,cv2.MORPH_CLOSE,kernel)
      
    # Remove salt and pepper noise with a median filter
    gray = cv2.medianBlur(gray,5)
    
    # If first frame, we need to initialize it.
    if first_frame is None:
        
      first_frame = gray
      
      # Clear the stream in preparation for the next frame
      raw_capture.truncate(0)
      
      # Go to top of for loop
      continue
      
    # Calculate the absolute difference between the current frame
    # and the first frame
    absolute_difference = cv2.absdiff(first_frame, gray)

    # If a pixel is less than ##, it is considered black (background). 
    # Otherwise, it is white (foreground). 255 is upper limit.
    # Modify the number after absolute_difference as you see fit.
    _, absolute_difference = cv2.threshold(absolute_difference, 95, 255, cv2.THRESH_BINARY)

    # Find the contours of the object inside the binary image
    contours, hierarchy = cv2.findContours(absolute_difference,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE)[-2:]
    areas = [cv2.contourArea(c) for c in contours]
 
    # If there are no countours
    if len(areas) < 1:
 
      # Display the resulting frame
      cv2.imshow('Frame',image)
 
      # Wait for keyPress for 1 millisecond
      key = cv2.waitKey(1) & 0xFF
 
      # Clear the stream in preparation for the next frame
      raw_capture.truncate(0)
    
      # If "q" is pressed on the keyboard, 
      # exit this loop
      if key == ord("q"):
        break
    
      # Go to the top of the for loop
      continue
 
    else:
        
      # Find the largest moving object in the image
      max_index = np.argmax(areas)
      
    # Draw the bounding box
    cnt = contours[max_index]
    x,y,w,h = cv2.boundingRect(cnt)
    cv2.rectangle(image,(x,y),(x+w,y+h),(0,255,0),3)
 
    # Draw circle in the center of the bounding box
    x2 = x + int(w/2)
    y2 = y + int(h/2)
    cv2.circle(image,(x2,y2),4,(0,255,0),-1)
    
    # Calculate the center of the bounding box in centimeter coordinates
    # instead of pixel coordinates
    x2_cm = x2 * CM_TO_PIXEL
    y2_cm = y2 * CM_TO_PIXEL
    
    # Coordinates of the object in the camera reference frame
    cam_ref_coord = np.array([[x2_cm],
                              [y2_cm],
                              [0.0],
                              [1]])
    
    # Coordinates of the object in base reference frame
    coord_base_frame = homgen_0_c @ cam_ref_coord
 
    # Print the centroid coordinates (we'll use the center of the
    # bounding box) on the image
    text = "x: " + str(coord_base_frame[0][0]) + ", y: " + str(coord_base_frame[1][0])
    cv2.putText(image, text, (x2 - 10, y2 - 10),
      cv2.FONT_HERSHEY_SIMPLEX, 0.5, (0, 255, 0), 2)
         
    # Display the resulting frame
    cv2.imshow("Frame",image)
    
    # Wait for keyPress for 1 millisecond
    key = cv2.waitKey(1) & 0xFF
 
    # Clear the stream in preparation for the next frame
    raw_capture.truncate(0)
    
    # If "q" is pressed on the keyboard, 
    # exit this loop
    if key == ord("q"):
      break

# Close down windows
cv2.destroyAllWindows()

Run the code.

Then place a quarter on the dry erase board. You should see that the x and y coordinates of the quarter relative to the base frame are printed to the screen.

Then place a quarter on the dry erase board. You should see that the x and y coordinates of the quarter relative to the base frame are printed to the screen.

I am placing the quarter at x = 4 and y = 9. The text on the screen should now display the coordinates of the quarter in the base frame coordinates.

The first time I ran this code, my x coordinate was accurate, but my y coordinate was not. I modified the y displacement value until I got something in the ballpark of x =4 and y = 9 for the coordinates printed to the screen. In the end, my displacement value was 24.4 cm instead of 23.0 cm (which is what it was originally).

Thus, here was my final equation for converting camera coordinates to robotic base frame coordinates:

Where z₀ = z_c = 0 cm.

Pretty cool!

Case 2: Camera Lens Is Not Parallel To the Surface

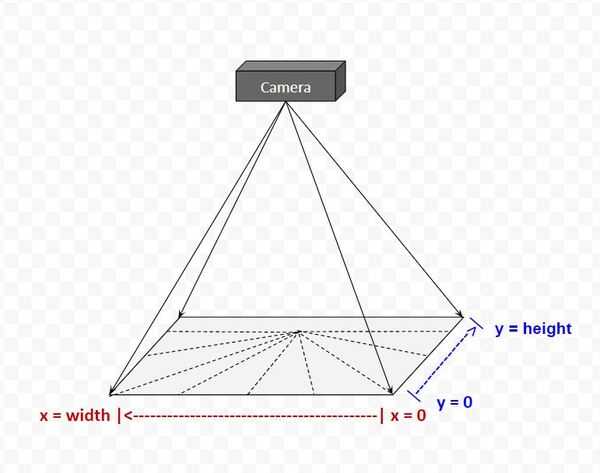
Up until now, we have assumed that the camera lens is always parallel to the underlying surface like this.

What happens if it isn’t, and instead the camera lens is looking down on the surface at some angle. You can imagine that in the real world, this situation is quite common. 

Consider this humanoid robot for example. This robot might have some sort of camera inside his helmet. Any surface that he looks at that is in front of his body will likely be from some angle.

Also, in real-world use cases, a physical grid is usually not present. Instead, the structured light technique is used to project a known grid pattern on a surface in order to help the robot determine the coordinates of an object.

You can see an example of structured light developed at the NASA Jet Propulsion Laboratory on the left side of this image.

A robot that looks at structured light would also see it from an angle. So, what changes in this case?

Previously in this tutorial, we assumed that the pixel-to-centimeter conversion factor will be the same in the x and y directions. This assumption only holds true, however, if the camera lens is directly overhead and parallel to the grid surface. This all changes when the camera is looking at a surface from an angle.

One way we can solve this problem is to derive (based on observation) a function that takes as input the pixel coordinates of an object (as seen by the camera) and outputs the (x₀,y₀) real-world coordinates in centimeters (i.e. the robotic arm base frame).

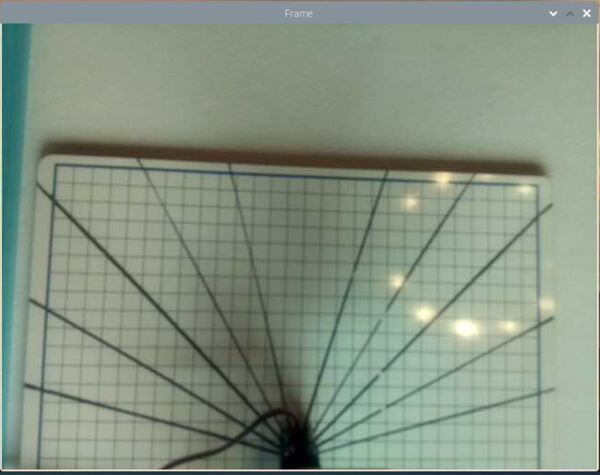
If you look at the image below, you can see that the pixel-to-centimeter conversion factor in the y (and x) direction is larger at the bottom of the image than it is at the top. And since the squares on the dry-erase board look more like rectangles, you know that the pixel-to-centimeter conversion factor is different in the x (horizontal) and y directions (vertical).

Example

Let’s do a real example, so you can see how to do this.

Create an Equation to Map Camera Pixel Y Coordinates to Global Reference Frame Y Coordinates in Centimeters

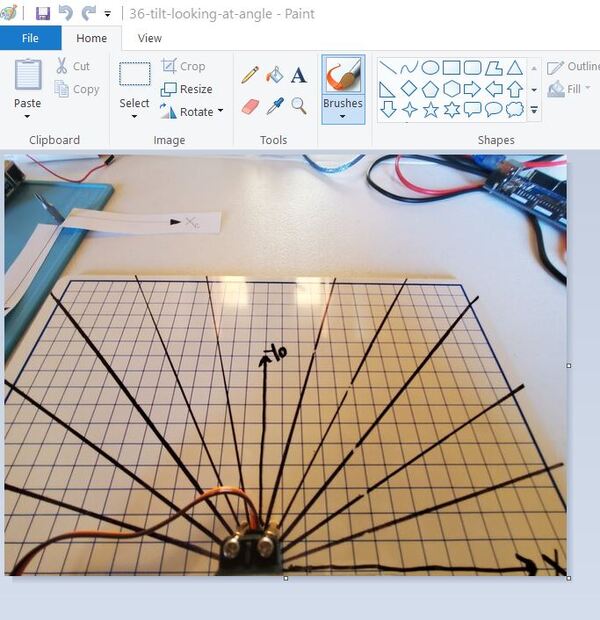
Open a snapshot from the tilted camera frame in a photo editing program like Microsoft Paint. My image is 640 pixels wide and 480 pixels in height. 

You can see in the bottom-left of Microsoft Paint how the program spits out the pixel location of my cursor. Make sure that whatever photo editing program you’re using gives you the ability to see pixel locations.

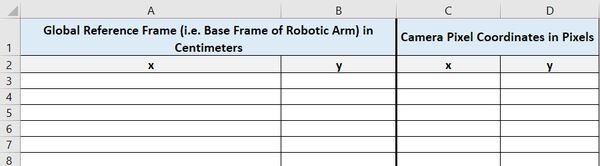
Open a blank spreadsheet. I’m using Microsoft Excel.

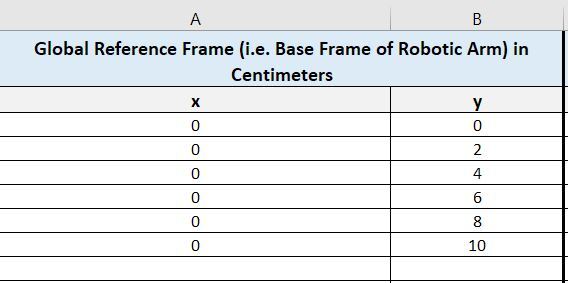
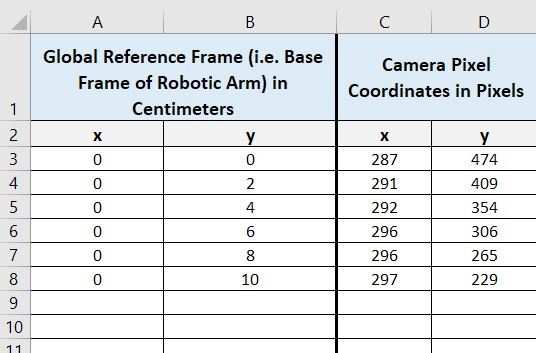
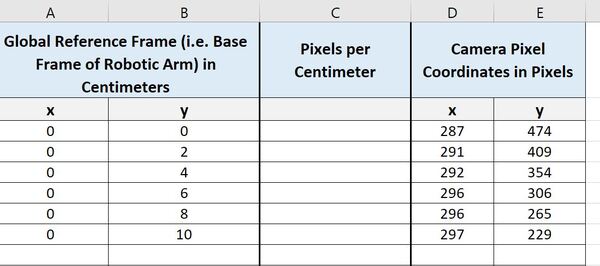
Create four columns:

• x in Column A (Global Reference Frame coordinates in cm)
• y in Column B (Global Reference Frame coordinates in cm)
• x in Column A (Camera Pixel coordinates)
• y in Column B (Camera Pixel coordinates)

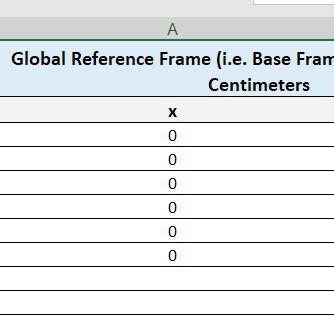
We will start by making x=0 and then finding the corresponding y.

Let’s fill in y with some evenly spaced values.

Take your cursor and place it on top of each global reference frame coordinate, and record the corresponding pixel value.

Now we want to find an equation that can convert camera pixel y coordinates to global reference frame y coordinates.

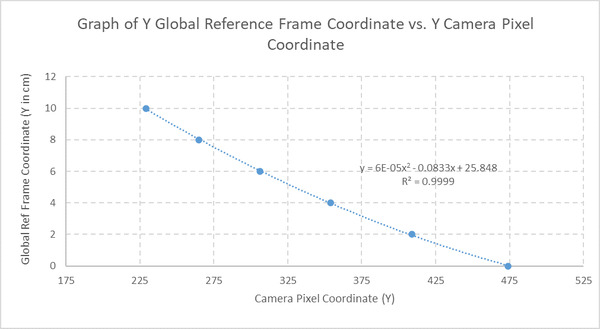
Plot the data. Here is how it looks.

I will right-click on the data points and add a trendline. I will place a checkmark near the “Display Equation on chart” and “Display R-squared value” options. I want to have a good R-squared value. This value shows how well my trendline fits the data. The closer it is to 1, the better.

A Polynomial best-fit line of Order 2 gives me an R-squared value of around 0.9999, so let’s go with this equation.

(Global Reference Frame Y Coordinate in cm) = 0.00006*(Camera Pixel Y Coordinate)² – 0.0833*(Camera Pixel Y Coordinate) + 25.848

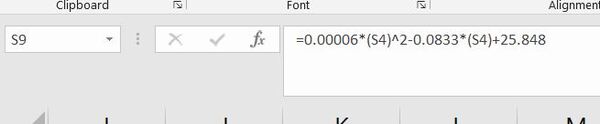
Now, let’s enter this formula into our spreadsheet.

I’m going to test the equation by choosing a random y pixel value and seeing what the y coordinate would be in centimeters.

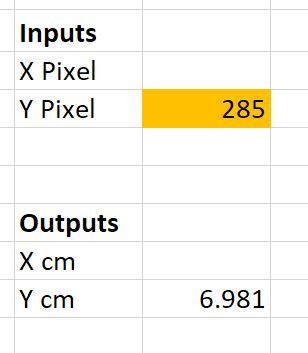
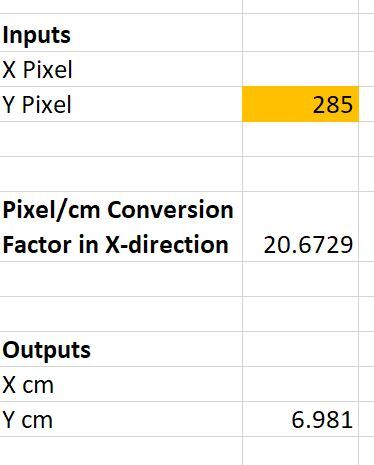
Go back to MS Paint. I’m going to put the cursor over (x=0 cm, y=7 cm) and then record what the y pixel value is.

I get a y pixel value of 285 when I put my cursor over this location. Let’s see what the equation spits out:

I calculated 6.981 cm. I expected to get a y value of 7 cm, so this is right around what I expected.

Create an Equation to Map Camera Pixel Y and X Coordinates to Global Reference Frame X Coordinates in Centimeters

Now let’s see how we can get the x position in centimeters. To do this, we need to do an interim step. Since the pixel-to-centimeter conversion factor in the x-direction varies along the y-axis, we need to find out the pixel-to-centimeter conversion factor in the x-direction for our original list of global reference frame y centimeter values.

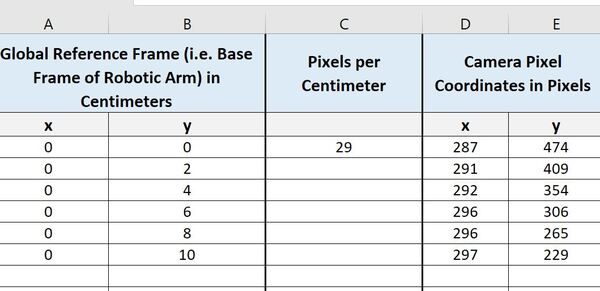
Go to the spreadsheet and insert a column to the right of the Y values for the global reference frame. We will label this column Pixels per Centimeter.

Let’s start at y = 0 cm. The pixel value there for x is 287. Now, we go 1 cm over to the right (i.e. each square is 1 cm in length) and find an x pixel value of 316. Therefore, for y = 0 cm, the pixel-to-centimeter conversion factor in the x direction is:

(316 pixels – 287 pixels) / 1 cm = 29 pixels/cm  

I’ll write that in the spreadsheet.

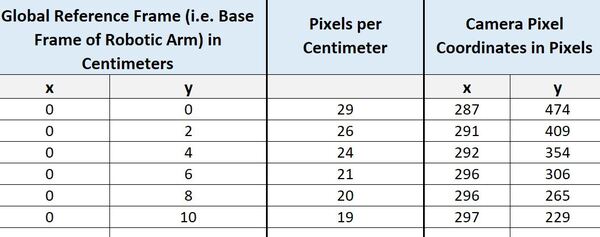
Now, do the same thing for all values of y in your spreadsheet.

Here is what my table now looks like:

Now what we want to do is create an equation that takes as input the global reference frame y value in centimeters and outputs the pixel-to-centimeter conversion factor along the x-direction.

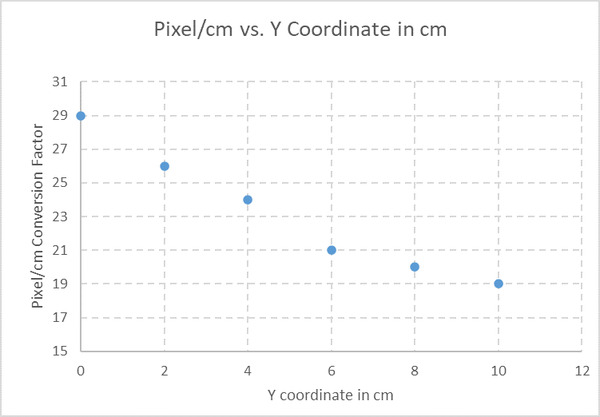
Here is the plot of the data:

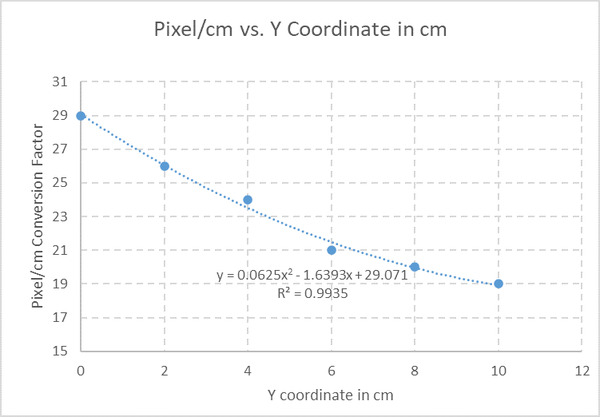
I will add a polynomial trendline of Order 2 and the R-squared value to see how well this line fits the data.

Our equation is:

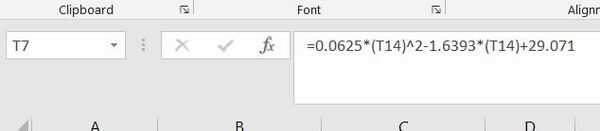
Pixel/cm Conversion Factor in the x-direction = 0.0625 * (Global Reference Frame Y Coordinate in cm)² -1.6393 * (Global Reference Frame Y Coordinate in cm) + 29.071

Let’s add this to our spreadsheet.

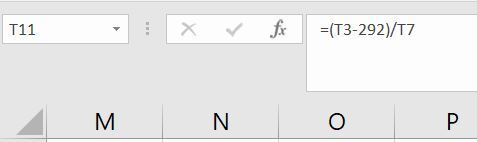
Now to find the x position in centimeters of an object in the camera frame, we need to take the x position in pixels as input, subtract the x pixel position of the centerline (i.e. when ≈ 292 pixels…which is the average of the highest and lowest x pixel coordinates of the centerline) and then divide by the pixel-to-centimeter conversion factor (along the x-direction for the corresponding y cm position). In other words:

Global Reference Frame X Coordinate in cm = ((Camera Pixel X Coordinate) – (X Pixel Coordinate of the Centerline))/ (Pixel/cm Conversion Factor in the x-direction)

I will add this formula to the spreadsheet.

Putting It All Together

Let’s test our math out to see what we get.

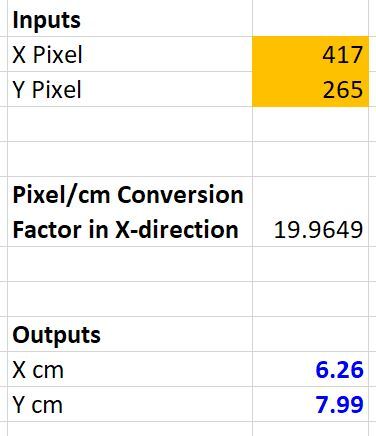
Go over to MS Paint or whatever photo editor you’re using. Select a random point on the grid. I’ll select the point (x = 6 cm, y = 8 cm). MS Paint tells me that the pixel value at this location is: (x = 417 px, y = 265 px). 

I’ll plug 417 and 265 into the spreadsheet as inputs.

You can see that our formula spit out:

• Global Reference Frame X Coordinate in cm: 6.26
• Global Reference Frame Y Coordinate in cm: 7.99

This result is pretty close to what we expected.

Congratulations! You now know what to do if you have a camera lens that is tilted relative to the plane of a gridded surface. No need to memorize this process. When you face this problem in the future, just come back to the steps I’ve outlined in this tutorial, and go through them one-by-one.

That’s it for this tutorial. Keep building!

References

Credit to Professor Angela Sodemann for teaching me this stuff. Dr. Sodemann is an excellent teacher (She runs a course on RoboGrok.com). 

In this tutorial, I’ll show you how to convert camera pixels to real-world coordinates (in centimeters). A common use case for this is in robotics (e.g. along a conveyor belt in a factory) where you want to pick up an object from one location and place it in another location using nothing but a robotic arm and an overhead camera.

Prerequisites

To complete this tutorial, it is helpful if you have completed the following prerequisites. If you haven’t that is fine. You can still follow the process I will explain below.

• You have set up Raspberry Pi with the Raspbian Operating System.
• You have OpenCV and a Raspberry Camera Module Installed.
• You know how to determine the pixel location of an object in a real-time video stream.
• You completed this tutorial to build a two degree of freedom robotic arm (Optional). My eventual goal is to be able to move this robotic arm to the location of an object that is placed somewhere in its workspace. The location of the object will be determined by the overhead Raspberry Pi camera.

You Will Need

Here are some extra components you’ll need if you want to follow along with the physical setup we put together in the prerequisites (above).

• 1 x VELCRO Brand Thin Clear Mounting Squares 12-pack | 7/8 Inch (you can also use Scotch tape).
• 1 x Overhead Video Stand Phone Holder
• 10 x 1cm Grid Write N Wipe Boards (check eBay….also search Amazon for ‘Centimeter Grid Dry Erase Board’) 
• 1 x Ruler that can measure in centimeters (or measuring tape)

Mount the Camera Module on the Overhead Video Stand Phone Holder (Optional)

Grab the Overhead Video Stand Phone Holder and place it above the grid like this.

Using some Velcro adhesives or some tape, attach the camera to the holder’s end effector so that it is pointing downward towards the center of the grid.

Here is how my video feed looks.

I am running the program on this page (test_video_capture.py). I’ll retype the code here:

# Credit: Adrian Rosebrock
# https://www.pyimagesearch.com/2015/03/30/accessing-the-raspberry-pi-camera-with-opencv-and-python/

# import the necessary packages
from picamera.array import PiRGBArray # Generates a 3D RGB array
from picamera import PiCamera # Provides a Python interface for the RPi Camera Module
import time # Provides time-related functions
import cv2 # OpenCV library

# Initialize the camera
camera = PiCamera()

# Set the camera resolution
camera.resolution = (640, 480)

# Set the number of frames per second
camera.framerate = 32

# Generates a 3D RGB array and stores it in rawCapture
raw_capture = PiRGBArray(camera, size=(640, 480))

# Wait a certain number of seconds to allow the camera time to warmup
time.sleep(0.1)

# Capture frames continuously from the camera
for frame in camera.capture_continuous(raw_capture, format="bgr", use_video_port=True):
    
    # Grab the raw NumPy array representing the image
    image = frame.array
    
    # Display the frame using OpenCV
    cv2.imshow("Frame", image)
    
    # Wait for keyPress for 1 millisecond
    key = cv2.waitKey(1) & 0xFF
    
    # Clear the stream in preparation for the next frame
    raw_capture.truncate(0)
    
    # If the `q` key was pressed, break from the loop
    if key == ord("q"):
        break

What is Our Goal?

Assuming you’ve completed the prerequisites, you know how to find the location of an object in the field of view of a camera, and you know how to express that location in terms of the pixel location along both the x-axis (width) and y-axis (height) of the video frame.

In a real use case, if we want a robotic arm to automatically pick up an object that enters its workspace, we need some way to tell the robotic arm where the object is. In order to do that, we have to convert the object’s position in the camera reference frame to a position that is relative to the robotic arm’s base frame. 

Once we know the object’s position relative to the robotic arm’s base frame, all we need to do is to calculate the inverse kinematics to set the servo motors to the angles that will enable the end effector of the robotic arm to reach the object.

What is the Field of View?

Before we get started, let’s take a look at what field of view means.

The field of view for our Raspberry Pi camera is the extent of the observable world that it can see at a given point in time.

In the figure below, you can see a schematic of the setup I have with the Raspberry Pi. In this perspective, we are in front of the Raspberry Pi camera. 

In the Python code, we set the size of the video frame to be 640 pixels in width and 480 pixels in height. Thus, the matrix that describes the field of view of our camera has 480 rows and 640 columns. 

From the perspective of the camera (i.e. camera reference frame), the first pixel in an image is at (x=0, y=0), which is in the far upper-left. The last pixel (x = 640, y = 480) is in the far lower-right.

Calculate the Centimeter to Pixel Conversion Factor

The first thing you need to do is to run test_video_capture.py.

Now, grab a ruler and measure the width of the frame in centimeters. It is hard to see in the image below, but my video frame is about 32 cm in width.

We know that in pixel units, the frame is 640 pixels in width. 

Therefore, we have the following conversion factor from centimeters to pixels:

32 cm / 640 pixels = 0.05 cm / pixel

We will assume the pixels are square-shaped and the camera lens is parallel to the underlying surface so we can use the same conversion factor for both the x (width) and y (height) axes of the camera frame.

When you’re done, you can close down test_video_capture.py.

Test Your Conversion Factor

Now, let’s test this conversion factor of 0.05 cm / pixel.

Write the following code in your favorite Python IDE or text editor (I’m using Gedit).

This program is the absolute_difference_method.py code we wrote on this post with some small changes. This code detects an object and then prints its center to the video frame. I called this program absolute_difference_method_cm.py.

# Author: Addison Sears-Collins
# Description: This algorithm detects objects in a video stream
#   using the Absolute Difference Method. The idea behind this 
#   algorithm is that we first take a snapshot of the background.
#   We then identify changes by taking the absolute difference 
#   between the current video frame and that original 
#   snapshot of the background (i.e. first frame). 

# import the necessary packages
from picamera.array import PiRGBArray # Generates a 3D RGB array
from picamera import PiCamera # Provides a Python interface for the RPi Camera Module
import time # Provides time-related functions
import cv2 # OpenCV library
import numpy as np # Import NumPy library

# Initialize the camera
camera = PiCamera()

# Set the camera resolution
camera.resolution = (640, 480)

# Set the number of frames per second
camera.framerate = 30

# Generates a 3D RGB array and stores it in rawCapture
raw_capture = PiRGBArray(camera, size=(640, 480))

# Wait a certain number of seconds to allow the camera time to warmup
time.sleep(0.1)

# Initialize the first frame of the video stream
first_frame = None

# Create kernel for morphological operation. You can tweak
# the dimensions of the kernel.
# e.g. instead of 20, 20, you can try 30, 30
kernel = np.ones((20,20),np.uint8)

# Centimeter to pixel conversion factor
# I measured 32.0 cm across the width of the field of view of the camera.
CM_TO_PIXEL = 32.0 / 640

# Capture frames continuously from the camera
for frame in camera.capture_continuous(raw_capture, format="bgr", use_video_port=True):
    
    # Grab the raw NumPy array representing the image
    image = frame.array

    # Convert the image to grayscale
    gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    
    # Close gaps using closing
    gray = cv2.morphologyEx(gray,cv2.MORPH_CLOSE,kernel)
      
    # Remove salt and pepper noise with a median filter
    gray = cv2.medianBlur(gray,5)
    
    # If first frame, we need to initialize it.
    if first_frame is None:
        
      first_frame = gray
      
      # Clear the stream in preparation for the next frame
      raw_capture.truncate(0)
      
      # Go to top of for loop
      continue
      
    # Calculate the absolute difference between the current frame
    # and the first frame
    absolute_difference = cv2.absdiff(first_frame, gray)

    # If a pixel is less than ##, it is considered black (background). 
    # Otherwise, it is white (foreground). 255 is upper limit.
    # Modify the number after absolute_difference as you see fit.
    _, absolute_difference = cv2.threshold(absolute_difference, 50, 255, cv2.THRESH_BINARY)

    # Find the contours of the object inside the binary image
    contours, hierarchy = cv2.findContours(absolute_difference,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE)[-2:]
    areas = [cv2.contourArea(c) for c in contours]
 
    # If there are no countours
    if len(areas) < 1:
 
      # Display the resulting frame
      cv2.imshow('Frame',image)
 
      # Wait for keyPress for 1 millisecond
      key = cv2.waitKey(1) & 0xFF
 
      # Clear the stream in preparation for the next frame
      raw_capture.truncate(0)
    
      # If "q" is pressed on the keyboard, 
      # exit this loop
      if key == ord("q"):
        break
    
      # Go to the top of the for loop
      continue
 
    else:
        
      # Find the largest moving object in the image
      max_index = np.argmax(areas)
      
    # Draw the bounding box
    cnt = contours[max_index]
    x,y,w,h = cv2.boundingRect(cnt)
    cv2.rectangle(image,(x,y),(x+w,y+h),(0,255,0),3)
 
    # Draw circle in the center of the bounding box
    x2 = x + int(w/2)
    y2 = y + int(h/2)
    cv2.circle(image,(x2,y2),4,(0,255,0),-1)
	
    # Calculate the center of the bounding box in centimeter coordinates
    # instead of pixel coordinates
    x2_cm = x2 * CM_TO_PIXEL
    y2_cm = y2 * CM_TO_PIXEL
 
    # Print the centroid coordinates (we'll use the center of the
    # bounding box) on the image
    text = "x: " + str(x2_cm) + ", y: " + str(y2_cm)
    cv2.putText(image, text, (x2 - 10, y2 - 10),
      cv2.FONT_HERSHEY_SIMPLEX, 0.5, (0, 255, 0), 2)
         
    # Display the resulting frame
    cv2.imshow("Frame",image)
    
    # Wait for keyPress for 1 millisecond
    key = cv2.waitKey(1) & 0xFF
 
    # Clear the stream in preparation for the next frame
    raw_capture.truncate(0)
    
    # If "q" is pressed on the keyboard, 
    # exit this loop
    if key == ord("q"):
      break

# Close down windows
cv2.destroyAllWindows()

To get the object’s center in centimeter coordinates rather than pixel coordinates, we had to add the cm-to-pixel conversion factor to our code. 

When you first launch the code, be sure there are no objects in the field of view and that the camera is not moving. Also, make sure that the level of light is fairly uniform across the board with no moving shadows (e.g. such as from the sun shining through a nearby window). Then place an object in the field of view and record the object’s x and y coordinate. 

Here is the camera output when I first run the code:

Here is the output after I place my wallet in the field of view:

• x-coordinate of the wallet in centimeters: 12.1 cm
• y-coordinate of the wallet in centimeters: 12.75 cm

Get a ruler, and measure the object’s x coordinate (measure from the left-side of the camera frame) in centimeters, and see if that matches up with the x-value printed to the camera frame.

Get a ruler, and measure the object’s y coordinate (measure from the top of the camera frame) in centimeters, and see if that matches up with the y-value printed to the camera frame.

The measurements should match up pretty well.

That’s it. Keep building!

References

Credit to Professor Angela Sodemann for teaching me this stuff. Dr. Sodemann is an excellent teacher (She runs a course on RoboGrok.com).