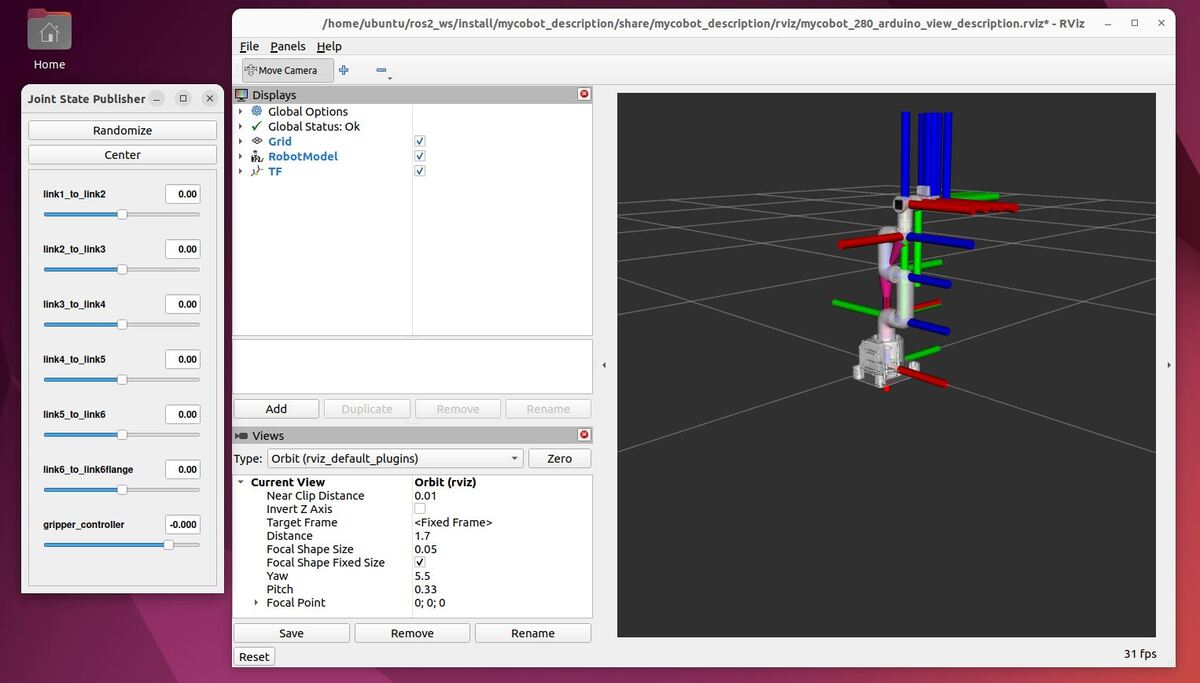
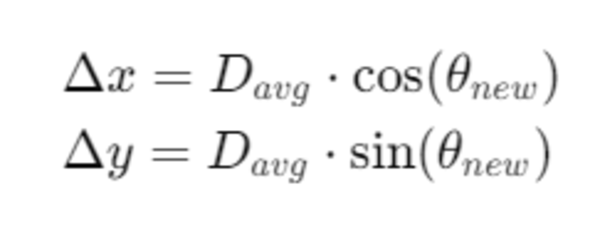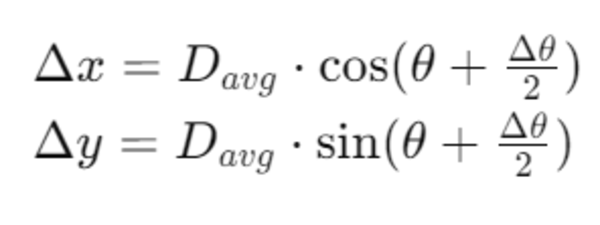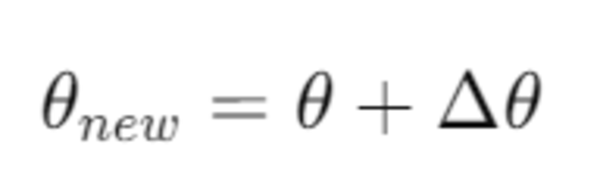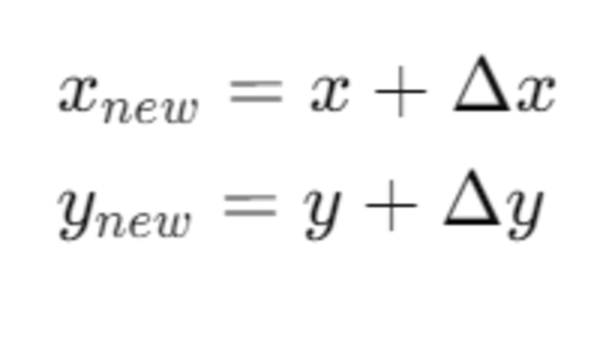In this tutorial, I will guide you through the process of simulating and performing basic control of a robotic arm in Gazebo. By the end of this tutorial, you will be able to build this:
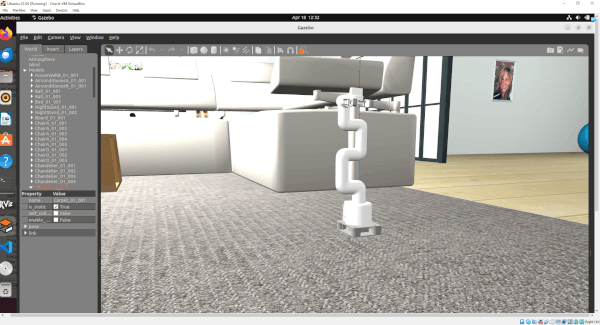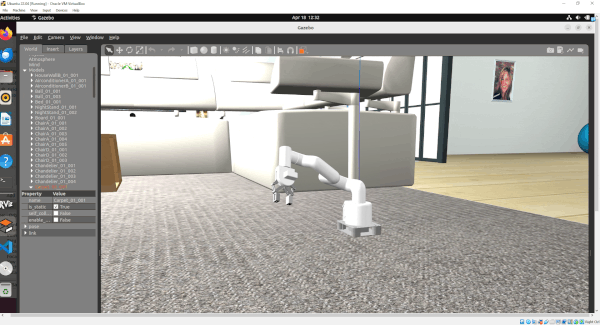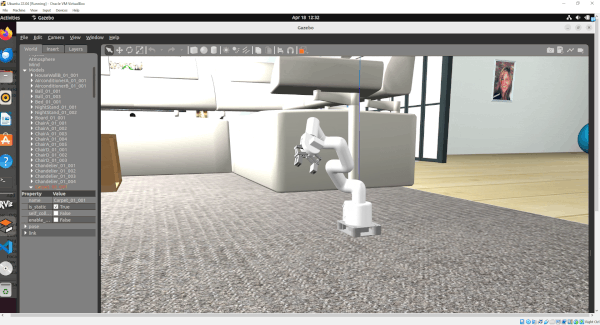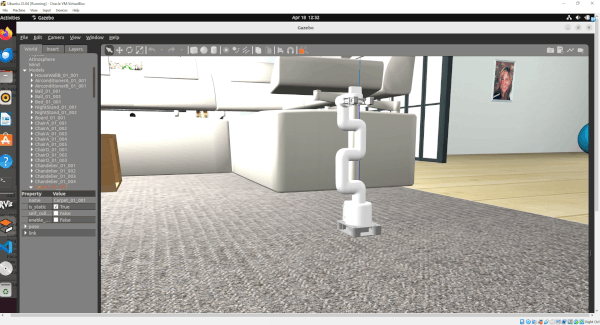
Gazebo is a robotics simulator that enables the testing and development of robots in a virtual environment. It supports a wide range of robots and integrates seamlessly with ROS 2, facilitating the transition from simulation to real-world application. This makes Gazebo an essential tool for roboticists aiming to prototype and refine algorithms efficiently.
Before we begin, I should advise you that Gazebo has been going through a lot of changes over the last several years. These changes are discussed here. They have changed the name several times and have not fully ported all the ROS plugins from the old classic Gazebo to the new Gazebo simulation engine (some folks still call the new Gazebo, “Ignition”, although it is no longer called Ignition).
For this reason, I have split this tutorial into two sections: Gazebo (new version) and Gazebo Classic (old version). I will show you how to launch and perform basic control of a robotic arm using both Gazebo versions.
Prerequisites
- You understand what a joint and link are.
- You have created a ROS 2 workspace.
- You know what a ROS 2 package is.
- You have created a URDF file for a simulated robotic arm that you want to use in Gazebo. I will be using the myCobot 280 for Arduino by Elephant Robotics.
- If you are using a virtual machine on Ubuntu, I recommend you use Oracle VirtualBox instead of VMWare. I had a lot of issues on VMWare that prevented me from running Gazebo.
- I am using ROS 2 Iron, the most recent version at the time of writing this tutorial, but you are welcome to use other versions of ROS 2 if you prefer.
All my code for this project is located here on GitHub.
Gazebo (new version)
Install Gazebo, ros_gz, and numpy
The first thing we need to do is to install the package that handles the integration between ROS 2 and Gazebo. The name of this package is ros_gz. Here is the GitHub repository, and here are the official installation instructions. Let’s walk through the steps together.
I am using ROS 2 Iron, but regardless of the ROS 2 version you are using, you will need to open a terminal window, and type this command to install the package:
sudo apt-get install ros-${ROS_DISTRO}-ros-gzType Y and press Enter to install the package.
The command above installs ros_gz and the correct version of Gazebo for your ROS 2 version.
Now install Numpy, a scientific computing library for Python.
sudo apt install python3 python3-pippip3 install numpyTest Your Installation
To test your installation, we will run the example from this part of the repo.
ros2 launch ros_gz_sim gz_sim.launch.py gz_args:="shapes.sdf"Here is what you should see:
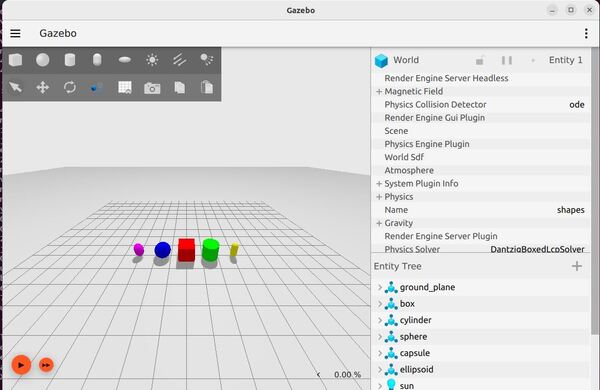
Feel free to run the other demos which you can find here.
When you run each demo, you can explore the topics by typing:
ros2 topic listCreate World Files
The first thing we need to do is to create an environment for your simulated robot.
We are going to create a new package named mycobot_gazebo.
cd ~/ros2_ws/src/mycobot_ros2/ros2 pkg create --build-type ament_cmake --license BSD-3-Clause mycobot_gazebocd mycobot_gazeboCreate a worlds folder:
mkdir worldsAlso, create other folders we will need later:
mkdir launchmkdir modelsNow let’s create our world. This first world we will create is an empty world.
cd worldsgedit empty.worldAdd this code.
<?xml version="1.0" ?>
<sdf version="1.6">
<world name="default">
<!-- Plugin for simulating physics -->
<plugin
filename="gz-sim-physics-system"
name="gz::sim::systems::Physics">
</plugin>
<!-- Plugin for handling user commands -->
<plugin
filename="gz-sim-user-commands-system"
name="gz::sim::systems::UserCommands">
</plugin>
<!-- Plugin for broadcasting scene updates -->
<plugin
filename="gz-sim-scene-broadcaster-system"
name="gz::sim::systems::SceneBroadcaster">
</plugin>
<!-- To add realistic gravity, do: 0.0 0.0 -9.8, otherwise do 0.0 0.0 0.0 -->
<gravity>0.0 0.0 -9.8</gravity>
<!-- Include a model of the Sun from an external URI -->
<include>
<uri>
https://fuel.gazebosim.org/1.0/OpenRobotics/models/Sun
</uri>
</include>
<!-- Include a model of the Ground Plane from an external URI -->
<include>
<uri>
https://fuel.gazebosim.org/1.0/OpenRobotics/models/Ground Plane
</uri>
</include>
<!-- Define scene properties -->
<scene>
<shadows>false</shadows>
</scene>
</world>
</sdf>
Save the file, and close it.
Now let’s create a world called house.world.
gedit house.worldAdd this code.
Save the file, and close it.
Create a models folder. These models are physical objects that will exist inside your house world.
cd ..mkdir modelscd modelsMake sure you put these models inside your models folder.
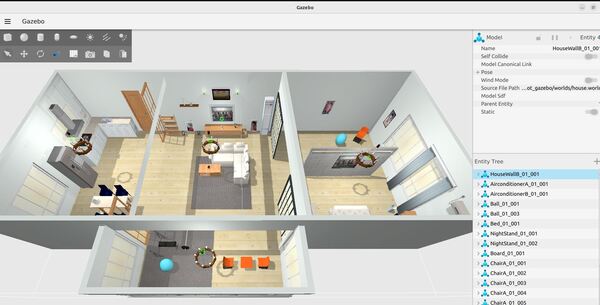
Create a URDF File
Now let’s create our URDF file. A URDF (Unified Robot Description Format) file is an XML format file used to describe the physical configuration and properties of a robot in a structured and standard way.
cd ~/ros2_ws/src/mycobot_ros2/mycobot_gazebo/mkdir urdfcd urdfgedit mycobot_280_gazebo.urdf.xacroAdd this code. Then save and close.
You will notice I added plugins at the end of the URDF File. Here is a list of plugins that can be added to our URDF file to create extra functionality.
The two plugins I added are the JointStatePublisher and the JointPositionController.
The JointStatePublisher publishes the state of all joints in a robot, including positions (radians or meters), velocities (radians per second or meters per second), and efforts (Nm or N) as a sensor_msgs/JointState message.
The JointPositionController subscribes to target joint angles (i.e. positions) as a std_msgs/Float64 message (i.e. a floating-point number like 0.36).
I had some issues loading the xacro format directly into Gazebo. Everything worked perfectly when I converted the xacro file to URDF format. Let’s convert our xacro file to URDF format now.
xacro mycobot_280_gazebo.urdf.xacro > mycobot_280_gazebo.urdfThe resulting file should look like this.
Create the Parameters File
To enable Gazebo to communicate with to ROS 2 topics and vice versa, you need to set up a parameter file that bridges the topics between the two platforms. You can see tutorials of how this works here on GitHub (for ROS 2 Iron and older)
Open a new terminal window, and type:
cd ~/ros2_ws/src/mycobot_ros2/mycobot_gazebo/mkdir configcd configgedit ros_gz_bridge.yamlAdd this code, and then save the file.
Create the Launch File
Let’s create a launch file to spawn both our world and our robotic arm.
cd ~/ros2_ws/src/mycobot_ros2/mycobot_gazebo/mkdir launchcd launchgedit mycobot_280_arduino_bringup_gazebo.launch.pyAdd this code.
# Author: Addison Sears-Collins
# Date: April 14, 2024
# Description: Launch a robotic arm in Gazebo
import os
from launch import LaunchDescription
from launch.actions import AppendEnvironmentVariable, DeclareLaunchArgument, IncludeLaunchDescription
from launch.conditions import IfCondition
from launch.launch_description_sources import PythonLaunchDescriptionSource
from launch.substitutions import Command, LaunchConfiguration, PythonExpression
from launch_ros.actions import Node
from launch_ros.parameter_descriptions import ParameterValue
from launch_ros.substitutions import FindPackageShare
def generate_launch_description():
# Constants for paths to different files and folders
package_name_description = 'mycobot_description'
package_name_gazebo = 'mycobot_gazebo'
default_robot_name = 'mycobot_280'
gazebo_launch_file_path = 'launch'
gazebo_models_path = 'models'
ros_gz_bridge_config_file_path = 'config/ros_gz_bridge.yaml'
rviz_config_file_path = 'rviz/mycobot_280_arduino_view_description.rviz'
urdf_file_path = 'urdf/mycobot_280_gazebo.urdf'
world_file_path = 'worlds/empty.world' # e.g. 'world/empty.world', 'world/house.world'
# Set the path to different files and folders.
pkg_ros_gz_sim = FindPackageShare(package='ros_gz_sim').find('ros_gz_sim')
pkg_share_description = FindPackageShare(package=package_name_description).find(package_name_description)
pkg_share_gazebo = FindPackageShare(package=package_name_gazebo).find(package_name_gazebo)
default_ros_gz_bridge_config_file_path = os.path.join(pkg_share_gazebo, ros_gz_bridge_config_file_path)
default_rviz_config_path = os.path.join(pkg_share_description, rviz_config_file_path)
default_urdf_model_path = os.path.join(pkg_share_gazebo, urdf_file_path)
gazebo_launch_file_path = os.path.join(pkg_share_gazebo, gazebo_launch_file_path)
gazebo_models_path = os.path.join(pkg_share_gazebo, gazebo_models_path)
world_path = os.path.join(pkg_share_gazebo, world_file_path)
# Launch configuration variables specific to simulation
headless = LaunchConfiguration('headless')
robot_name = LaunchConfiguration('robot_name')
rviz_config_file = LaunchConfiguration('rviz_config_file')
urdf_model = LaunchConfiguration('urdf_model')
use_robot_state_pub = LaunchConfiguration('use_robot_state_pub')
use_rviz = LaunchConfiguration('use_rviz')
use_sim_time = LaunchConfiguration('use_sim_time')
use_simulator = LaunchConfiguration('use_simulator')
world = LaunchConfiguration('world')
# Set the default pose
x = LaunchConfiguration('x')
y = LaunchConfiguration('y')
z = LaunchConfiguration('z')
roll = LaunchConfiguration('roll')
pitch = LaunchConfiguration('pitch')
yaw = LaunchConfiguration('yaw')
# Declare the launch arguments
declare_robot_name_cmd = DeclareLaunchArgument(
name='robot_name',
default_value=default_robot_name,
description='The name for the robot')
declare_rviz_config_file_cmd = DeclareLaunchArgument(
name='rviz_config_file',
default_value=default_rviz_config_path,
description='Full path to the RVIZ config file to use')
declare_simulator_cmd = DeclareLaunchArgument(
name='headless',
default_value='False',
description='Display the Gazebo GUI if False, otherwise run in headless mode')
declare_urdf_model_path_cmd = DeclareLaunchArgument(
name='urdf_model',
default_value=default_urdf_model_path,
description='Absolute path to robot urdf file')
declare_use_robot_state_pub_cmd = DeclareLaunchArgument(
name='use_robot_state_pub',
default_value='True',
description='Whether to start the robot state publisher')
declare_use_rviz_cmd = DeclareLaunchArgument(
name='use_rviz',
default_value='True',
description='Whether to start RVIZ')
declare_use_sim_time_cmd = DeclareLaunchArgument(
name='use_sim_time',
default_value='true',
description='Use simulation (Gazebo) clock if true')
declare_use_simulator_cmd = DeclareLaunchArgument(
name='use_simulator',
default_value='True',
description='Whether to start Gazebo')
declare_world_cmd = DeclareLaunchArgument(
name='world',
default_value=world_path,
description='Full path to the world model file to load')
declare_x_cmd = DeclareLaunchArgument(
name='x',
default_value='0.0',
description='x component of initial position, meters')
declare_y_cmd = DeclareLaunchArgument(
name='y',
default_value='0.0',
description='y component of initial position, meters')
declare_z_cmd = DeclareLaunchArgument(
name='z',
default_value='0.05',
description='z component of initial position, meters')
declare_roll_cmd = DeclareLaunchArgument(
name='roll',
default_value='0.0',
description='roll angle of initial orientation, radians')
declare_pitch_cmd = DeclareLaunchArgument(
name='pitch',
default_value='0.0',
description='pitch angle of initial orientation, radians')
declare_yaw_cmd = DeclareLaunchArgument(
name='yaw',
default_value='0.0',
description='yaw angle of initial orientation, radians')
# Specify the actions
set_env_vars_resources = AppendEnvironmentVariable(
'GZ_SIM_RESOURCE_PATH',
gazebo_models_path)
# Start Gazebo server
start_gazebo_server_cmd = IncludeLaunchDescription(
PythonLaunchDescriptionSource(
os.path.join(pkg_ros_gz_sim, 'launch', 'gz_sim.launch.py')),
condition=IfCondition(use_simulator),
launch_arguments={'gz_args': ['-r -s -v4 ', world], 'on_exit_shutdown': 'true'}.items())
# Start Gazebo client
start_gazebo_client_cmd = IncludeLaunchDescription(
PythonLaunchDescriptionSource(
os.path.join(pkg_ros_gz_sim, 'launch', 'gz_sim.launch.py')),
launch_arguments={'gz_args': '-g -v4 '}.items(),
condition=IfCondition(PythonExpression([use_simulator, ' and not ', headless])))
# Subscribe to the joint states of the robot, and publish the 3D pose of each link.
robot_description_content = ParameterValue(Command(['xacro ', urdf_model]), value_type=str)
start_robot_state_publisher_cmd = Node(
condition=IfCondition(use_robot_state_pub),
package='robot_state_publisher',
executable='robot_state_publisher',
name='robot_state_publisher',
output='screen',
parameters=[{
'use_sim_time': use_sim_time,
'robot_description': robot_description_content}])
# Launch RViz
start_rviz_cmd = Node(
condition=IfCondition(use_rviz),
package='rviz2',
executable='rviz2',
name='rviz2',
output='screen',
arguments=['-d', rviz_config_file])
# Spawn the robot
start_gazebo_ros_spawner_cmd = Node(
package='ros_gz_sim',
executable='create',
arguments=[
'-name', robot_name,
'-file', urdf_model,
'-x', x,
'-y', y,
'-z', z,
'-R', roll,
'-P', pitch,
'-Y', yaw
],
output='screen')
# Bridge ROS topics and Gazebo messages for establishing communication
start_gazebo_ros_bridge_cmd = Node(
package='ros_gz_bridge',
executable='parameter_bridge',
parameters=[{
'config_file': default_ros_gz_bridge_config_file_path,
}],
output='screen'
)
# Create the launch description and populate
ld = LaunchDescription()
# Declare the launch options
ld.add_action(declare_robot_name_cmd)
ld.add_action(declare_rviz_config_file_cmd)
ld.add_action(declare_simulator_cmd)
ld.add_action(declare_urdf_model_path_cmd)
ld.add_action(declare_use_robot_state_pub_cmd)
ld.add_action(declare_use_rviz_cmd)
ld.add_action(declare_use_sim_time_cmd)
ld.add_action(declare_use_simulator_cmd)
ld.add_action(declare_world_cmd)
ld.add_action(declare_x_cmd)
ld.add_action(declare_y_cmd)
ld.add_action(declare_z_cmd)
ld.add_action(declare_roll_cmd)
ld.add_action(declare_pitch_cmd)
ld.add_action(declare_yaw_cmd)
# Add any actions
ld.add_action(set_env_vars_resources)
ld.add_action(start_gazebo_server_cmd)
ld.add_action(start_gazebo_client_cmd)
ld.add_action(start_robot_state_publisher_cmd)
ld.add_action(start_rviz_cmd)
ld.add_action(start_gazebo_ros_spawner_cmd)
ld.add_action(start_gazebo_ros_bridge_cmd)
return ld
Save the file, and close it.
Edit package.xml
Now let’s modify our package.xml file to update the package dependencies.
cd ~/ros2_ws/src/mycobot_ros2/mycobot_gazebo/gedit package.xmlAdd this code. Save the file, and then close it.
Update CMakeLists.txt
Go to the CMakeLists.txt, and make sure it looks like this:
cd ~/ros2_ws/src/mycobot_ros2/mycobot_gazebo/gedit CMakeLists.txtYou can comment out or remove any folders or scripts in CMakeLists.txt that we have not yet created in this tutorial (e.g. test_set_joint_position_publisher.py). Be sure to do this before running “colcon build” below.
Save the file, and close it.
cd ~/ros2_ws/Make sure all dependencies are installed.
rosdep install --from-paths src --ignore-src -r -yBuild the package.
colcon buildsource ~/.bashrcLaunch the World and URDF Files Together
Run the launch file using the following command:
ros2 launch mycobot_gazebo mycobot_280_arduino_bringup_gazebo.launch.pyHere is the output using the empty.world file:
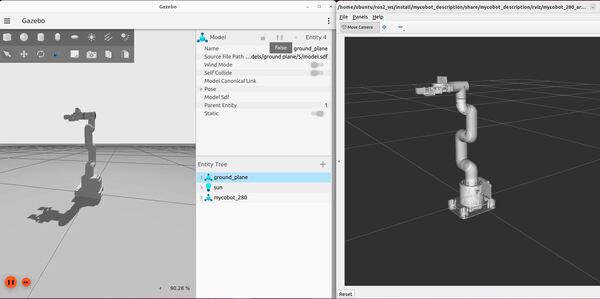
Here is the output using the house.world file. You might see a pop up asking if you would like to Force Quit Gazebo…just wait and be patient for everything to load (house.world is full of SDF models):
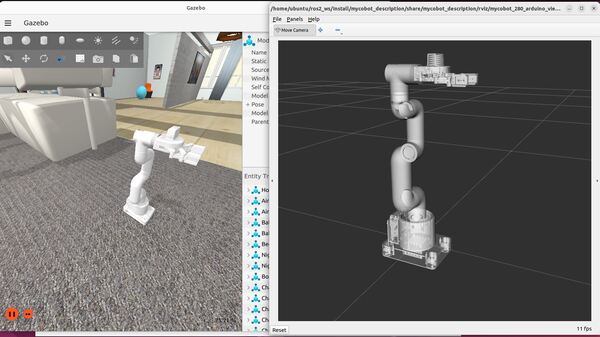
To see a list of active topics, type:
ign topic -lTo see the options, you can type:
ign topic -helpMove the Robotic Arm Manually
I could not get the JointTrajectoryController to work in this new Gazebo. As I mentioned earlier, things are moving fast over at Gazebo, and not all the plugins have been transitioned over. However, I was able to get the JointPositionController to work and make the arm move.
To send joint angles to the robot using Gazebo, type this in a terminal window (in future versions of Gazebo, you will replace “ign” with “gz” below:
ign topic -t /model/mycobot_280/joint/link1_to_link2/0/cmd_pos -m ignition.msgs.Double -p "data: -2.0"To send joint angles to the robot using ROS 2, type this in a terminal window:
ros2 topic pub -1 /model/mycobot_280/joint/link1_to_link2/cmd_pos std_msgs/msg/Float64 '{data: -2.0}'Move the Robotic Arm Using a Script
Let’s create a ROS 2 node that can loop through a list of joint positions to simulate the robotic arm moving from the home position to a goal location and then back to home, repeatedly.
cd ~/ros2_ws/src/mycobot_ros2/mycobot_gazebo/mkdir mycobot_gazebocd mycobot_gazebogedit __init__.pyAdd this code, and then close it.
cd ..mkdir scriptscd scriptsgedit test_set_joint_position_publisher.pyAdd this code:
#! /usr/bin/env python3
"""
Description:
ROS 2: Executes a sample trajectory for a robotic arm in Gazebo
-------
Publishing Topics (ROS 2):
Desired goal positions for joints on a robotic arm
/model/mycobot_280/joint/link1_to_link2/cmd_pos - std_msgs/Float64
/model/mycobot_280/joint/link2_to_link3/cmd_pos - std_msgs/Float64
/model/mycobot_280/joint/link3_to_link4/cmd_pos - std_msgs/Float64
/model/mycobot_280/joint/link4_to_link5/cmd_pos - std_msgs/Float64
/model/mycobot_280/joint/link5_to_link6/cmd_pos - std_msgs/Float64
/model/mycobot_280/joint/link6_to_link6flange/cmd_pos - std_msgs/Float64
/model/mycobot_280/joint/gripper_controller/cmd_pos - std_msgs/Float64
/model/mycobot_280/joint/gripper_base_to_gripper_left2/cmd_pos - std_msgs/Float64
/model/mycobot_280/joint/gripper_left3_to_gripper_left1/cmd_pos - std_msgs/Float64
/model/mycobot_280/joint/gripper_base_to_gripper_right3/cmd_pos - std_msgs/Float64
/model/mycobot_280/joint/gripper_base_to_gripper_right2/cmd_pos - std_msgs/Float64
/model/mycobot_280/joint/gripper_right3_to_gripper_right1/cmd_pos - std_msgs/Float64
-------
Author: Addison Sears-Collins
Date: April 18, 2024
"""
import numpy as np
import rclpy # Python client library for ROS 2
from rclpy.node import Node # Handles the creation of nodes
from std_msgs.msg import Float64 # Import the Float64 message
# Define constants
names_of_joints = [ 'link1_to_link2',
'link2_to_link3',
'link3_to_link4',
'link4_to_link5',
'link5_to_link6',
'link6_to_link6flange',
'gripper_controller',
'gripper_base_to_gripper_left2',
'gripper_left3_to_gripper_left1',
'gripper_base_to_gripper_right3',
'gripper_base_to_gripper_right2',
'gripper_right3_to_gripper_right1']
class BasicJointPositionPublisher(Node):
"""This class executes a sample trajectory for a robotic arm
"""
def __init__(self):
""" Constructor.
"""
# Initialize the class using the constructor
super().__init__('basic_joint_position_publisher')
# Create a publisher for each joint
self.position_publishers = [
self.create_publisher(Float64, f'/model/mycobot_280/joint/{name}/cmd_pos', 1)
for name in names_of_joints
]
self.timer_period = 0.05 # seconds
self.timer = self.create_timer(self.timer_period, self.timer_callback)
# Starting position and goal position for the robotic arm joints
self.start_position = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
self.end_position = [-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.7, -0.7, 0.7, 0.7, 0.7, -0.7]
# Number of steps to interpolate between positions
self.num_steps = 50
# Set the desired goal poses for the robotic arm.
self.positions = self.generate_positions(self.start_position, self.end_position)
# Keep track of the current trajectory we are executing
self.index = 0
# Indicate the direction of movement in the list of goal positions.
self.forward = True
def generate_positions(self, start_position, end_position):
"""
Generates positions along a path from start to end positions.
Args:
start_position (list): The starting position of the robotic arm.
end_position (list): The ending position of the robotic arm.
Returns:
list: A complete list of positions including all intermediate steps.
"""
# Example path including start and end, could be expanded to more waypoints
path_positions = [start_position, end_position]
all_positions = []
for i in range(len(path_positions) - 1):
interpolated = self.interpolate_positions(path_positions[i], path_positions[i + 1])
all_positions.extend(interpolated[:-1]) # Exclude the last to avoid duplicates
all_positions.append(path_positions[-1]) # Ensure the last position is included
return all_positions
def interpolate_positions(self, start, end):
"""
Linearly interpolates between two positions.
Args:
start (list): The starting position for interpolation.
end (list): The ending position for interpolation.
Returns:
list: A list of positions including the start, interpolated, and end positions.
"""
interpolated_positions = [start] # Initialize with the start position
step_vector = (np.array(end) - np.array(start)) / (self.num_steps + 1) # Calculate step vector
for step in range(1, self.num_steps + 1):
interpolated_position = np.array(start) + step * step_vector # Compute each interpolated position
interpolated_positions.append(interpolated_position.tolist()) # Append to the list
interpolated_positions.append(end) # Append the end position
return interpolated_positions
def timer_callback(self):
"""Set the goal pose for the robotic arm.
"""
# Publish the current position for each joint
for pub, pos in zip(self.position_publishers, self.positions[self.index]):
msg = Float64()
msg.data = pos
pub.publish(msg)
# Update the trajectory index
if self.forward:
if self.index < len(self.positions) - 1:
self.index = self.index + 1
else:
self.forward = False
else:
if self.index > 0:
self.index = self.index - 1
else:
self.forward = True
def main(args=None):
# Initialize the rclpy library
rclpy.init(args=args)
# Create the node
basic_joint_position_publisher = BasicJointPositionPublisher()
# Spin the node so the callback function is called.
rclpy.spin(basic_joint_position_publisher)
# Destroy the node
basic_joint_position_publisher.destroy_node()
# Shutdown the ROS client library for Python
rclpy.shutdown()
if __name__ == '__main__':
main()
Update your CMakeLists.txt to include this new script.
Now launch the robot. Wait for everything to come up, including RViz.
ros2 launch mycobot_gazebo mycobot_280_arduino_bringup_gazebo.launch.pyRun the basic joint position publisher to simulate movement for your robotic arm:
ros2 run mycobot_gazebo test_set_joint_position_publisher.pyYour arm will move from a home position to a goal position over and over again.
Gazebo (classic version)
Now let’s take a look at how to simulate and move a robotic arm using the classic version of Gazebo (which will reach end of life in 2025).
Install gazebo_ros_pkgs
Open a new terminal window, and install the packages that will enable you to use ROS 2 to interface with Gazebo Classic.
sudo apt install ros-$ROS_DISTRO-gazebo-ros-pkgsCreate a URDF File
cd ~/ros2_ws/src/mycobot_ros2/mycobot_gazebo/urdfgedit mycobot_280_classic_gazebo.urdf.xacroAdd this code. Then save and close.
Convert the xacro file to a URDF file:
xacro mycobot_280_classic_gazebo.urdf.xacro > mycobot_280_classic_gazebo.urdfCreate the Launch File
Let’s create a launch file to spawn both our world and our robotic arm.
cd ~/ros2_ws/src/mycobot_ros2/mycobot_gazebo/launchgedit mycobot_280_arduino_bringup_classic_gazebo.launch.pyAdd this code.
Save the file, and close it.
Create World Files
Create an environment for your simulated robot.
cd ~/ros2_ws/src/mycobot_ros2/mycobot_gazebo/worldsgedit empty_classic.worldAdd this code.
If you want gravity turned ON, the gravity line should look like this:
<gravity>0.0 0.0 -9.8</gravity>
If you want gravity turned OFF, the gravity line should look like this:
<gravity>0.0 0.0 0.0</gravity>
Save the file, and close it.
Now let’s create a world called house_classic.world.
gedit house_classic.worldAdd this code.
Save the file, and close it.
Launch the World and URDF Files Together
Build the Package.
cd ~/ros2_ws/rosdep install --from-paths src --ignore-src -r -ycolcon buildsource ~/.bashrcRun the launch file using the following command:
ros2 launch mycobot_gazebo mycobot_280_arduino_bringup_classic_gazebo.launch.pyHere is the output using the empty_classic.world file:
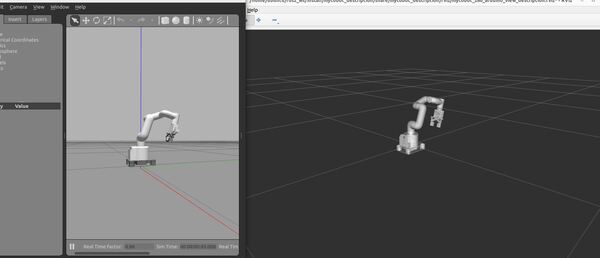
Here is the output using the house_classic.world file:
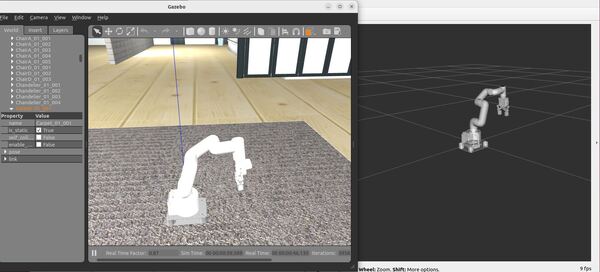
Move the Robotic Arm Manually
To make the robot move, you use this command:
ros2 topic pub -1 /set_joint_trajectory trajectory_msgs/msg/JointTrajectory "{header: {frame_id: base_link}, joint_names: [link1_to_link2, link2_to_link3, link3_to_link4, link4_to_link5, link5_to_link6, link6_to_link6flange, gripper_controller, gripper_base_to_gripper_left2, gripper_left3_to_gripper_left1, gripper_base_to_gripper_right3, gripper_base_to_gripper_right2, gripper_right3_to_gripper_right1], points: [{positions: [0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0]}]}"You can change the values in the positions array to move the robotic arm to different poses.
If you want to close the gripper, the gripper_controller position value needs to be -0.7.
ros2 topic pub -1 /set_joint_trajectory trajectory_msgs/msg/JointTrajectory "{header: {frame_id: base_link}, joint_names: [link1_to_link2, link2_to_link3, link3_to_link4, link4_to_link5, link5_to_link6, link6_to_link6flange, gripper_controller, gripper_base_to_gripper_left2, gripper_left3_to_gripper_left1, gripper_base_to_gripper_right3, gripper_base_to_gripper_right2, gripper_right3_to_gripper_right1], points: [{positions: [-1.345,-1.230,0.264,-0.296,0.389,-1.50,-0.7, -0.7, 0.7, 0.7, 0.7, -0.7]}]}"The two Gazebo plugins defined in the xacro file that make all this work are libgazebo_ros_joint_state_publisher.so (publishes the joint states from Gazebo to ROS 2) and libgazebo_ros_joint_pose_trajectory.so (subscribes to the desired goal poses for the arm that are sent from ROS 2 to Gazebo). That is all you need for basic arm control.
To close Gazebo, press CTRL + C on your keyboard.
Move the Robotic Arm Using a Script
Let’s create a ROS 2 node that can loop through a list of trajectories to simulate the arm moving from the home position to a goal location and then back to home.
cd ~/ros2_ws/src/mycobot_ros2/mycobot_gazebo/scriptsgedit test_set_joint_trajectory_publisher.pyAdd this code:
#! /usr/bin/env python3
"""
Description:
ROS 2: Executes a sample trajectory for a robotic arm in Gazebo Classic
-------
Publishing Topics (ROS 2):
Desired goal pose of a robotic arm
/set_joint_trajectory - trajectory_msgs/JointTrajectory
-------
Author: Addison Sears-Collins
Date: April 18, 2024
"""
import rclpy # Python client library for ROS 2
from rclpy.node import Node # Handles the creation of nodes
from trajectory_msgs.msg import JointTrajectory, JointTrajectoryPoint
from builtin_interfaces.msg import Duration
from std_msgs.msg import Header # Import the Header message
# Define constants
names_of_joints = [ 'link1_to_link2',
'link2_to_link3',
'link3_to_link4',
'link4_to_link5',
'link5_to_link6',
'link6_to_link6flange',
'gripper_controller',
'gripper_base_to_gripper_left2',
'gripper_left3_to_gripper_left1',
'gripper_base_to_gripper_right3',
'gripper_base_to_gripper_right2',
'gripper_right3_to_gripper_right1']
class BasicJointTrajectoryPublisher(Node):
"""This class executes a sample trajectory for a robotic arm
"""
def __init__(self):
""" Constructor.
"""
# Initialize the class using the constructor
super().__init__('basic_joint_trajectory_publisher')
# Create the publisher of the desired arm goal poses
self.pose_publisher = self.create_publisher(JointTrajectory, '/set_joint_trajectory', 1)
self.timer_period = 0.05 # seconds
self.timer = self.create_timer(self.timer_period, self.timer_callback)
self.frame_id = "base_link"
# Set the desired goal poses for the robotic arm.
# To make the code cleaner, I could have imported these positions from a yaml file.
self.positions = [
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.0269, -0.0246, 0.00528, -0.00592, 0.00778, -0.03, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.0538, -0.0492, 0.01056, -0.01184, 0.01556, -0.06, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.0807, -0.0738, 0.01584, -0.01776, 0.02334, -0.09, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.1076, -0.0984, 0.02112, -0.02368, 0.03112, -0.12, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.1345, -0.123, 0.0264, -0.0296, 0.0389, -0.15, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.1614, -0.1476, 0.03168, -0.03552, 0.04668, -0.18, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.1883, -0.1722, 0.03696, -0.04144, 0.05446, -0.21, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.2152, -0.1968, 0.04224, -0.04736, 0.06224, -0.24, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.2421, -0.2214, 0.04752, -0.05328, 0.07002, -0.27, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.269, -0.246, 0.0528, -0.0592, 0.0778, -0.3, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.2959, -0.2706, 0.05808, -0.06512, 0.08558, -0.33, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.3228, -0.2952, 0.06336, -0.07104, 0.09336, -0.36, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.3497, -0.3198, 0.06864, -0.07696, 0.10114, -0.39, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.3766, -0.3444, 0.07392, -0.08288, 0.10892, -0.42, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.4035, -0.369, 0.0792, -0.0888, 0.1167, -0.45, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.4304, -0.3936, 0.08448, -0.09472, 0.12448, -0.48, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.4573, -0.4182, 0.08976, -0.10064, 0.13226, -0.51, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.4842, -0.4428, 0.09504, -0.10656, 0.14004, -0.54, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.5111, -0.4674, 0.10032, -0.11248, 0.14782, -0.57, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.538, -0.492, 0.1056, -0.1184, 0.1556, -0.6, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.5649, -0.5166, 0.11088, -0.12432, 0.16338, -0.63, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.5918, -0.5412, 0.11616, -0.13024, 0.17116, -0.66, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.6187, -0.5658, 0.12144, -0.13616, 0.17894, -0.69, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.6456, -0.5904, 0.12672, -0.14208, 0.18672, -0.72, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.6725, -0.615, 0.132, -0.148, 0.1945, -0.75, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.6994, -0.6396, 0.13728, -0.15392, 0.20228, -0.78, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.7263, -0.6642, 0.14256, -0.15984, 0.21006, -0.81, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.7532, -0.6888, 0.14784, -0.16576, 0.21784, -0.84, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.7801, -0.7134, 0.15312, -0.17168, 0.22562, -0.87, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.807, -0.738, 0.1584, -0.1776, 0.2334, -0.9, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.8339, -0.7626, 0.16368, -0.18352, 0.24118, -0.93, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.8608, -0.7872, 0.16896, -0.18944, 0.24896, -0.96, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.8877, -0.8118, 0.17424, -0.19536, 0.25674, -0.99, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.9146, -0.8364, 0.17952, -0.20128, 0.26452, -1.02, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.9415, -0.861, 0.1848, -0.2072, 0.2723, -1.05, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.9684, -0.8856, 0.19008, -0.21312, 0.28008, -1.08, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-0.9953, -0.9102, 0.19536, -0.21904, 0.28786, -1.11, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-1.0222, -0.9348, 0.20064, -0.22496, 0.29564, -1.14, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-1.0491, -0.9594, 0.20592, -0.23088, 0.30342, -1.17, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-1.076, -0.984, 0.2112, -0.2368, 0.3112, -1.2, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-1.1029, -1.0086, 0.21648, -0.24272, 0.31898, -1.23, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-1.1298, -1.0332, 0.22176, -0.24864, 0.32676, -1.26, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-1.1567, -1.0578, 0.22704, -0.25456, 0.33454, -1.29, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-1.1836, -1.0824, 0.23232, -0.26048, 0.34232, -1.32, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-1.2105, -1.107, 0.2376, -0.2664, 0.3501, -1.35, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-1.2374, -1.1316, 0.24288, -0.27232, 0.35788, -1.38, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-1.2643, -1.1562, 0.24816, -0.27824, 0.36566, -1.41, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-1.2912, -1.1808, 0.25344, -0.28416, 0.37344, -1.44, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-1.3181, -1.2054, 0.25872, -0.29008, 0.38122, -1.47, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.07, -0.07, 0.07, 0.07, 0.07, -0.07],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.14, -0.14, 0.14, 0.14, 0.14, -0.14],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.21, -0.21, 0.21, 0.21, 0.21, -0.21],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.28, -0.28, 0.28, 0.28, 0.28, -0.28],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.35, -0.35, 0.35, 0.35, 0.35, -0.35],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.42, -0.42, 0.42, 0.42, 0.42, -0.42],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.49, -0.49, 0.49, 0.49, 0.49, -0.49],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.56, -0.56, 0.56, 0.56, 0.56, -0.56],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.63, -0.63, 0.63, 0.63, 0.63, -0.63],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.7, -0.7, 0.7, 0.7, 0.7, -0.7],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.7, -0.7, 0.7, 0.7, 0.7, -0.7],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.7, -0.7, 0.7, 0.7, 0.7, -0.7],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.7, -0.7, 0.7, 0.7, 0.7, -0.7],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.7, -0.7, 0.7, 0.7, 0.7, -0.7],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.7, -0.7, 0.7, 0.7, 0.7, -0.7],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.7, -0.7, 0.7, 0.7, 0.7, -0.7],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.7, -0.7, 0.7, 0.7, 0.7, -0.7],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.7, -0.7, 0.7, 0.7, 0.7, -0.7],
[-1.345, -1.23, 0.264, -0.296, 0.389, -1.5, -0.7, -0.7, 0.7, 0.7, 0.7, -0.7],
]
# Keep track of the current trajectory we are executing
self.index = 0
# Indicate the direction of movement in the list of goal positions.
self.forward = True
def timer_callback(self):
"""Set the goal pose for the robotic arm.
"""
# Create a new JointTrajectory message
msg = JointTrajectory()
msg.header = Header() # Initialize the header
msg.header.frame_id = self.frame_id
msg.joint_names = names_of_joints
# Create a JointTrajectoryPoint
point = JointTrajectoryPoint()
point.positions = self.positions[self.index]
point.time_from_start = Duration(sec=0, nanosec=int(self.timer_period * 1e9)) # Time to next position
msg.points.append(point)
self.pose_publisher.publish(msg)
# Move index forward or backward
if self.forward:
if self.index < len(self.positions) - 1:
self.index += 1
else:
self.forward = False
else:
if self.index > 0:
self.index -= 1
else:
self.forward = True
def main(args=None):
# Initialize the rclpy library
rclpy.init(args=args)
# Create the node
basic_joint_trajectory_publisher = BasicJointTrajectoryPublisher()
# Spin the node so the callback function is called.
rclpy.spin(basic_joint_trajectory_publisher)
# Destroy the node
basic_joint_trajectory_publisher.destroy_node()
# Shutdown the ROS client library for Python
rclpy.shutdown()
if __name__ == '__main__':
main()
Make sure to update your CMakeLists.txt file.
Build your package.
cd ~/ros2_ws/colcon buildsource ~/.bashrcNow launch the robot. Wait for everything to come up, including RViz.
ros2 launch mycobot_gazebo mycobot_280_arduino_bringup_classic_gazebo.launch.pyRun the basic joint trajectory publisher to simulate movement for your robotic arm:
ros2 run mycobot_gazebo test_set_joint_trajectory_publisher.pyThe output should look like the animated image at the beginning of this blog post.
Note that even though we have the “mimic” tag in the URDF file for the gripper, we still have to explicitly define all non-fixed joints in the URDF Gazebo plugins section in order for everything to work properly in Gazebo.
That’s it! Keep building!