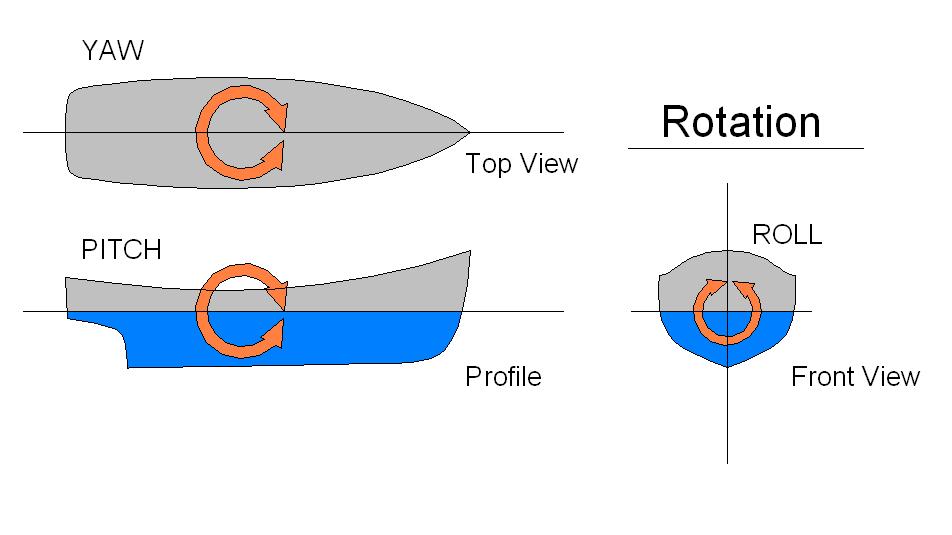
Given Euler angles of the following form….

Rotation about the x axis = roll angle = α
Rotation about the y-axis = pitch angle = β
Rotation about the z-axis = yaw angle = γ

…how do we convert this into a quaternion of the form (x, y, z, w) where w is the scalar (real) part and x, y, and z are the vector parts?

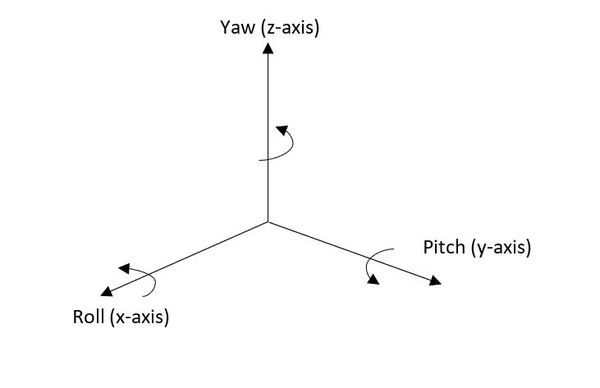
Doing this operation is important because ROS2 (and ROS) uses quaternions as the default representation for the orientation of a robot in 3D space.

Here is the Python code:

#! /usr/bin/env python3

# This program converts Euler angles to a quaternion.
# Author: AutomaticAddison.com

import numpy as np # Scientific computing library for Python

def get_quaternion_from_euler(roll, pitch, yaw):
  """
  Convert an Euler angle to a quaternion.
  
  Input
    :param roll: The roll (rotation around x-axis) angle in radians.
    :param pitch: The pitch (rotation around y-axis) angle in radians.
    :param yaw: The yaw (rotation around z-axis) angle in radians.

  Output
    :return qx, qy, qz, qw: The orientation in quaternion [x,y,z,w] format
  """
  qx = np.sin(roll/2) * np.cos(pitch/2) * np.cos(yaw/2) - np.cos(roll/2) * np.sin(pitch/2) * np.sin(yaw/2)
  qy = np.cos(roll/2) * np.sin(pitch/2) * np.cos(yaw/2) + np.sin(roll/2) * np.cos(pitch/2) * np.sin(yaw/2)
  qz = np.cos(roll/2) * np.cos(pitch/2) * np.sin(yaw/2) - np.sin(roll/2) * np.sin(pitch/2) * np.cos(yaw/2)
  qw = np.cos(roll/2) * np.cos(pitch/2) * np.cos(yaw/2) + np.sin(roll/2) * np.sin(pitch/2) * np.sin(yaw/2)

  return [qx, qy, qz, qw]

Example

Suppose a robot is on a flat surface. It has the following Euler angles:

Euler Angle (roll, pitch, yaw) = (0.0, 0.0, π/2) = (0.0, 0.0, 1.5708)

What is the robot’s orientation in quaternion format (x, y, z, w)?

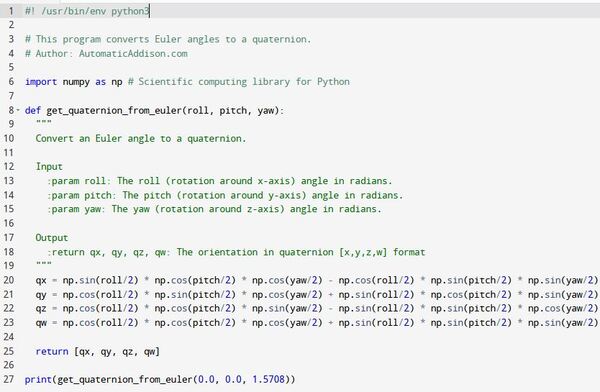
The program shows that the quaternion is:

Quaternion [x,y,z,w] = [0, 0, 0.7071, 0.7071]

And that’s all there is to it folks. That’s how you convert a Euler angles into a quaternion.