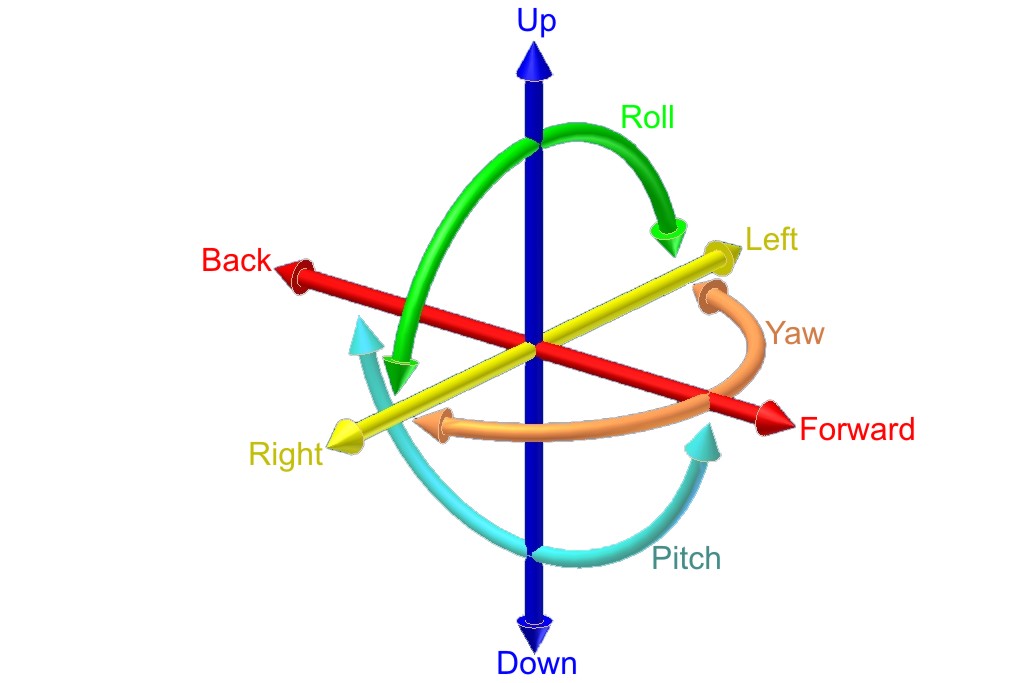
In robotics, we commonly represent the position of a robot in space using three axes:
- x-axis
- y-axis
- z-axis
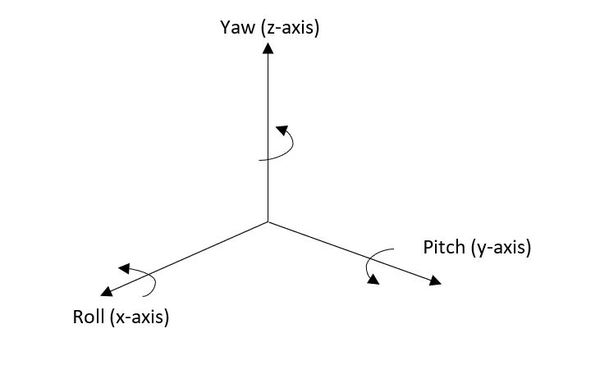
We represent rotation about each of these axes using the following standard names:
- roll (rotation about the x-axis)
- pitch (rotation about the y-axis)
- yaw (rotation about the z-axis)
Now, let’s say we have a 4-wheeled robot in space. The robot is moving in the +y direction as shown in the figure below. The robot turns slightly to the left, rotating around the z-axis.
Rotation about the z-axis is yaw rotation.
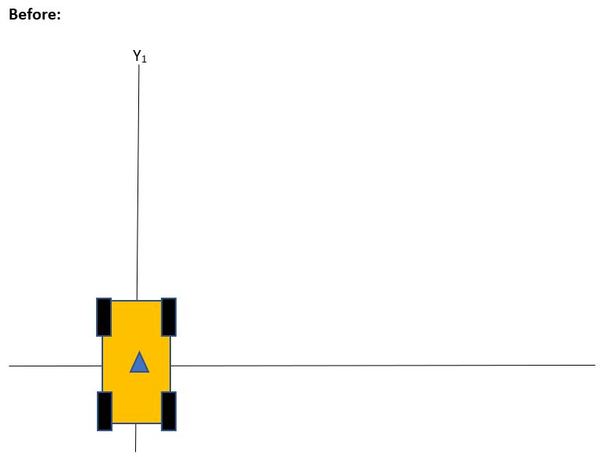
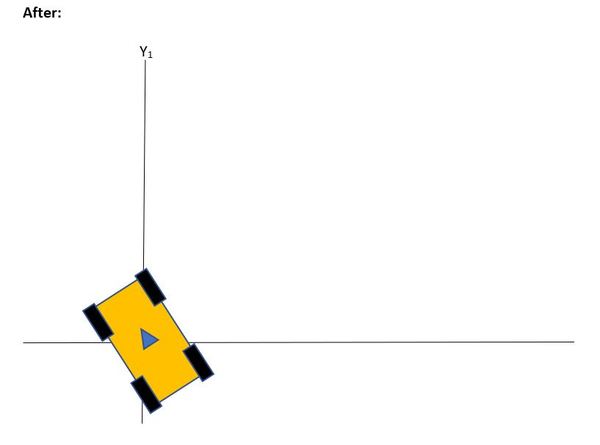
What would the new coordinate system look like from the robot’s perspective if we used just a 2D coordinate system (instead of a 3D coordinate system like we did above)?
Yaw rotation means the robot rotates about the z-axis in the counter-clockwise direction, so the robot’s new coordinate system would look like this (where the angle γ represents the amount of rotation of the coordinate axes in degrees or radians):
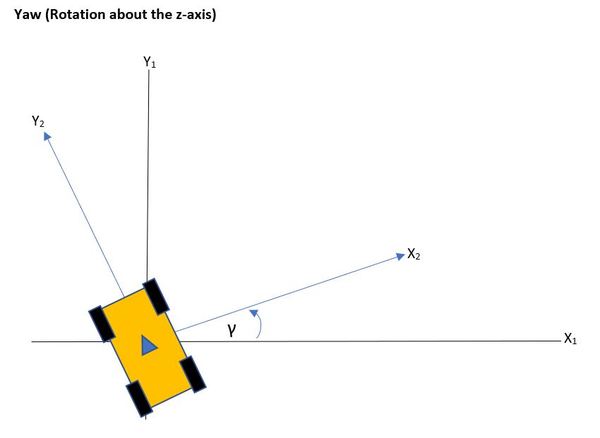
Note that the z-axis is coming right straight out of the page from that blue arrow above.
Now, here are the illustrations for the roll and pitch rotations using 2D coordinate systems:
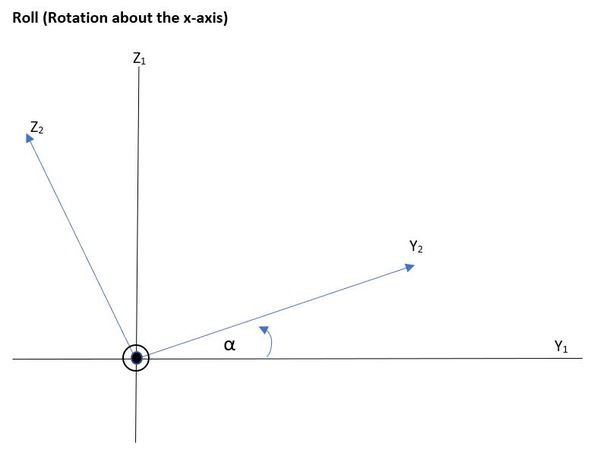
The x-axis is that black dot above. It is coming right straight out of the page.
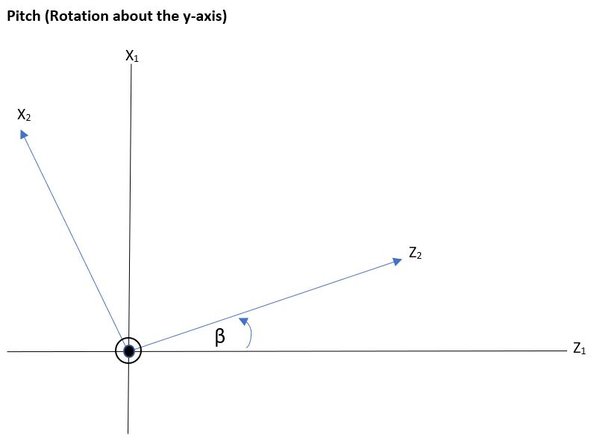
The y-axis is that black dot above. It is coming right straight out of the page.