How to Describe the Rotation of a Robot in 3D

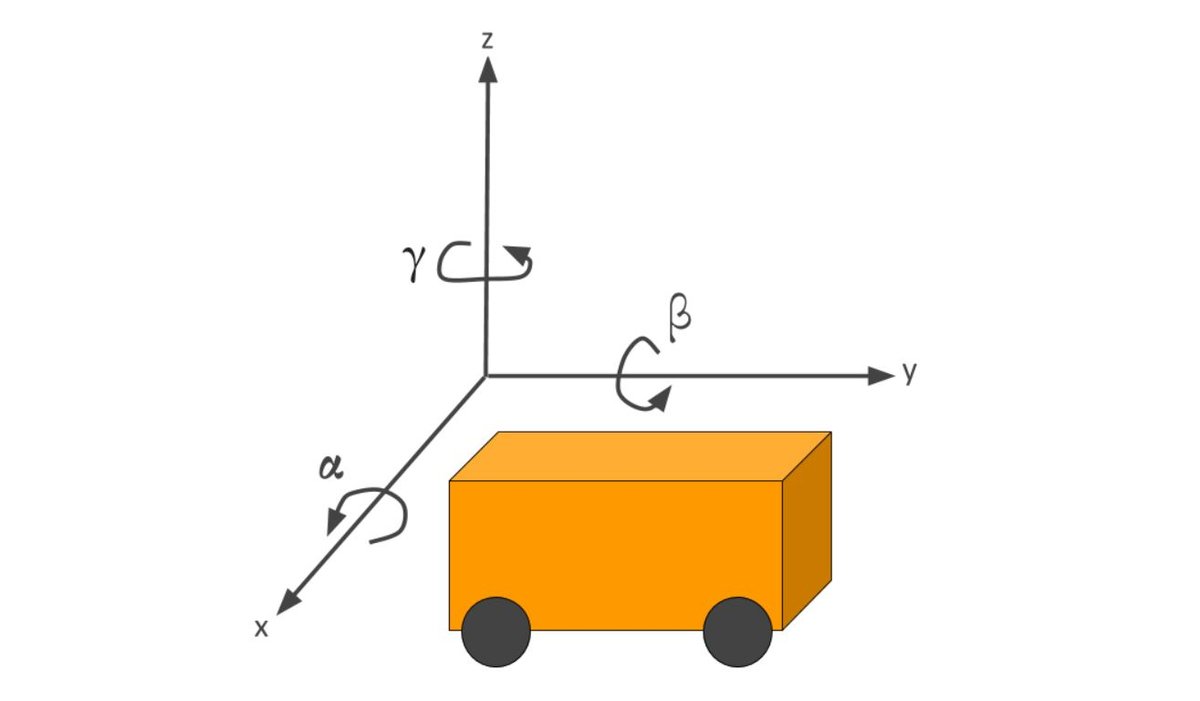
mobile_robot_in_3d

Before we get into how to describe the rotation of a robot in three dimensions, it is important you understand how to describe the rotation of a robot in two dimensions.

In my previous post, we learned how to calculate the coordinates of a point (or vector) in the 2D global reference frame given the coordinates of that point (or magnitude and direction of that vector) in the 2D robot (local) reference frame (i.e. the rotated coordinate system).

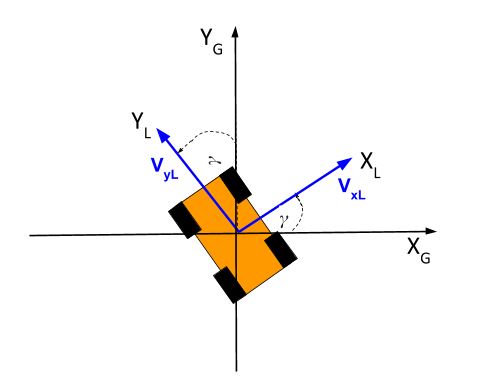
13-robot-coordinate-axes

Here is the equation we use to convert a point in the 2D local reference frame to a point in the 2D global reference frame (If you don’t know how to multiply matrices together, there are a bunch of videos on YouTube that walk through the process):

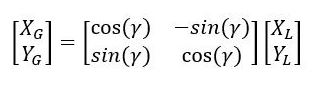
19-local-to-global-matrix-form

Here is the equation we use to convert velocity in the 2D local reference frame to velocity in the 2D global reference frame:

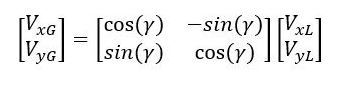
17-system-of-equations

The thing that makes all this possible is the two-dimensional rotation matrix:

18-rotation-matrix

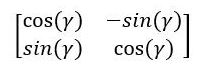
To describe the rotation of a robot in three dimensions, we need to use the three-dimensional rotation matrix. Let’s explore this now.

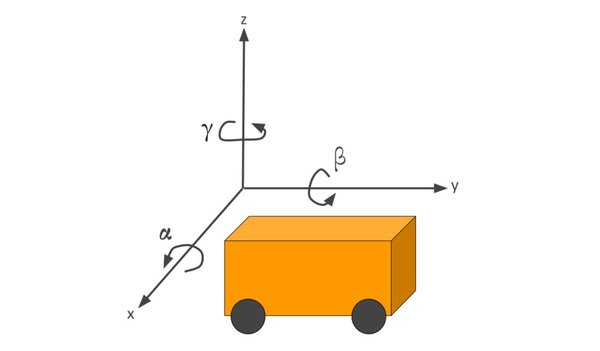
mobile_robot_in_3d-1

Table of Contents

Converting a Point (Or Vector) in the 3D Local Reference Frame to a Point in the 3D Global Reference Frame

In two dimensions, the only angle we had to worry about was γ. γ represents the amount of rotation (in degrees or radians) of the robot x-axis from the global x-axis, going in the counterclockwise direction.

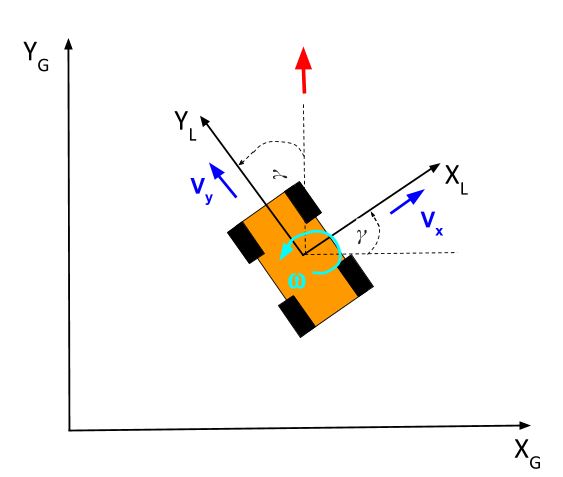
12-rotating-robot

γ is often called the yaw angle. It is the angle of rotation about the z-axis.

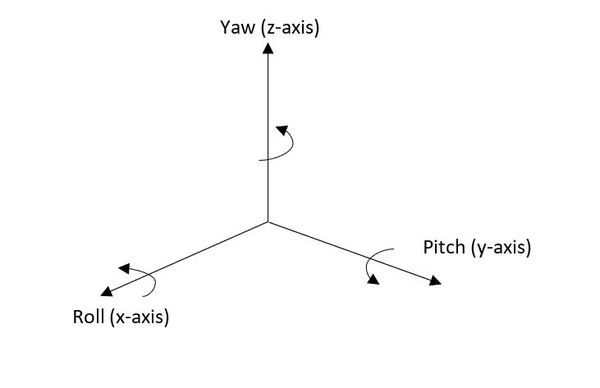
yaw_pitch_rollJPG

We need to add two more angles:

  • Rotation about the x axis = roll angle = α
  • Rotation about the y-axis = pitch angle = β

If you want to learn more about these angles, check out my post on roll, pitch, and yaw.

So, how do we derive the three-dimensional rotation matrix? What we need to do is calculate the rotation matrix for all rotations a robot can do in a three-dimensional space. Since there are three axes, there are three different rotations we need to account for: rotation about the x-axis, rotation about the y-axis, and rotation about the z-axis.

Return to Table of Contents

Yaw (Rotation about the z-axis)

Let’s start with rotation about the z-axis. Guess what? We already know that rotation matrix.

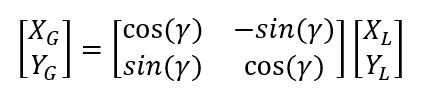
1-rotation-matrix

This is the two-dimensional case I explained at the beginning of this post. The x and y coordinates of a point in the robot reference frame will change when converted to coordinates in the global reference frame. However, the z coordinate will remain constant.

Here is the rotation matrix that takes care of rotation of a robot in 3D about the global z-axis:

2-yaw

Return to Table of Contents

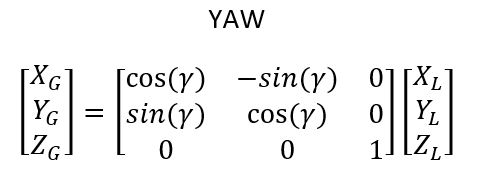
Pitch (Rotation about the y-axis)

When we rotate a point about the y-axis, the x and z coordinates of the point will change, but the y-coordinate will remain the same. 

Here is the rotation matrix that enables us to convert a point (or vector) in the local reference frame to a point (or vector) in the global reference frame when all we have is rotation of the robot about the global y-axis.

3-pitch

Return to Table of Contents

Roll (Rotation about the x-axis)

When we rotate a point about the x-axis, the y and z coordinates of the point will change, but the x-coordinate will remain the same. 

Here is the rotation matrix that enables us to convert a point (or vector) in the local reference frame to a point (or vector) in the global reference frame when all we have is rotation of the robot about the global x-axis.

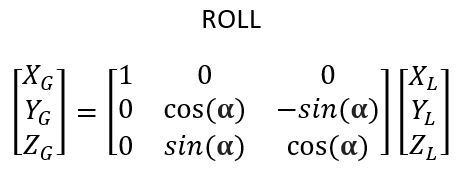
4-roll

Return to Table of Contents

Putting It All Together

Ok, so now we need to combine the three matrices above to calculate the full three-dimensional rotation matrix.

5-full-3d-rotation-matrix
6-3d-rotation-matrix-derivation
7-3d-rotation-matrix

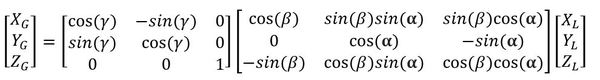
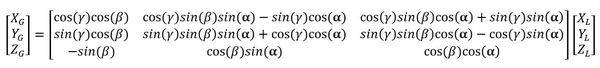
Three-Dimensional Rotation Matrix in Python Code

Here is a NumPy-based method that converts angles into a 3×3 rotation matrix like the one above. You can use this method in whatever code you want to write.

import numpy as np # NumPy library

def euler_rotation_matrix(alpha,beta,gamma):
    """
    Generate a full three-dimensional rotation matrix from euler angles

    Input
    :param alpha: The roll angle (radians) - Rotation around the x-axis
    :param beta: The pitch angle (radians) - Rotation around the y-axis
    :param alpha: The yaw angle (radians) - Rotation around the z-axis

    Output
    :return: A 3x3 element matix containing the rotation matrix. 
             This rotation matrix converts a point in the local reference 
             frame to a point in the global reference frame.

    """
    # First row of the rotation matrix
    r00 = np.cos(gamma) * np.cos(beta)
    r01 = np.cos(gamma) * np.sin(beta) * np.sin(alpha) - np.sin(gamma) * np.cos(alpha)
    r02 = np.cos(gamma) * np.sin(beta) * np.cos(alpha) + np.sin(gamma) * np.sin(alpha)
    
    # Second row of the rotation matrix
    r10 = np.sin(gamma) * np.cos(beta)
    r11 = np.sin(gamma) * np.sin(beta) * np.sin(alpha) + np.cos(gamma) * np.cos(alpha)
    r12 = np.sin(gamma) * np.sin(beta) * np.cos(alpha) - np.cos(gamma) * np.sin(alpha)
	
    # Third row of the rotation matrix
    r20 = -np.sin(beta)
    r21 = np.cos(beta) * np.sin(alpha)
    r22 = np.cos(beta) * np.cos(alpha)
	
    # 3x3 rotation matrix
    rot_matrix = np.array([[r00, r01, r02],
                           [r10, r11, r12],
                           [r20, r21, r22]])
						   
    return rot_matrix

def rotate(p1,alpha,beta,gamma):
    """
    Rotates a point p1 in 3D space in the local reference frame to 
    a point p2 in the global reference frame.

    Input
    :param p1: A 3 element array containing the position of a point in the 
              local reference frame (xL,yL,zL) 
    :param alpha: The roll angle (radians) - Rotation around the x-axis
    :param beta: The pitch angle (radians) - Rotation around the y-axis
    :param alpha: The yaw angle (radians) - Rotation around the z-axis

    Output
    :return: p2: A 3 element array containing the position of a point in the 
             global reference frame (xG,yG,zG)

    """
    p2 = euler_rotation_matrix(alpha, beta, gamma) @ p1
    return p2

def main():

    # Point that we want to rotate from local frame to global frame
    p1 = np.array([5,6,7])
    
    # Rotation angles
    alpha = (30/180.0)*np.pi
    beta =  (40/180.0)*np.pi
    gamma = (70/180.0)*np.pi

    print(f'local coordinates p1: {p1}')
    print(f'Rotated by Roll {alpha}, Pitch {beta}, Yaw: {gamma}')
    p2 = rotate(p1,alpha,beta,gamma)

    print(f'global coordinates p2:{p2}')

if __name__ == '__main__':
    main()

Return to Table of Contents

Example Calculation

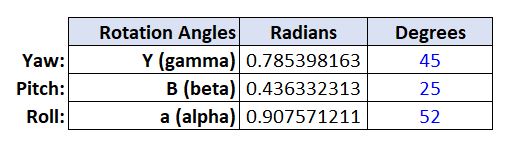
Let’s say that we have a point P2 (x,y,z) in the local reference frame that has coordinates (5,-2,7). It is rotated the following angles:

  • Yaw = 45°
  • Pitch = 25°
  • Roll = 52°

What is the full three-dimensional rotation matrix?

Remember our equation for the full three-dimensional rotation matrix.

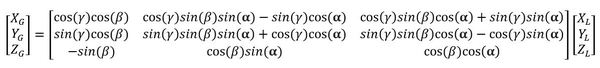
7-3d-rotation-matrix-1

We plug the numbers in the problem statement into this equation above.

1
2
3-calculated-rotation-matrix

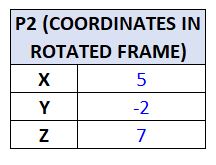
What are the coordinates of point P1 (x,y,z), which is the point P2 in terms of the global reference frame?

To get the coordinates of point P1, we need to multiply P2 by the rotation matrix we found above.

4

You should get the numbers in yellow.

5-new-coordinates

Return to Table of Contents

Converting a Point (Or Vector) in the 3D Global Reference Frame to a Point in the 3D Local Reference Frame

Below we are going to derive the equation that will enable you to convert a point (or vector) in the 3D global reference frame to a point (or vector) in the 3D local reference frame. In other words, we are going to calculate the three-dimensional inverse rotation matrix.

If you remember, when we derived the three-dimensional rotation matrix earlier in this post, we started out with this equation.

5-full-3d-rotation-matrix-1

You’ll notice that the first operation performed on a point in the local frame is to account for rotation about the x-axis (i.e. roll). Then we do pitch (rotation about the y-axis), and then we do yaw (rotation about the z-axis). This sequence of operations enables us to convert any point (or vector) in the 3D local reference frame to a point (or vector) in the 3D global reference frame. 

To calculate the inverse three-dimensional rotation matrix, we need to find the inverse of each of the three matrices and then perform the operations in reverse order. Let’s walk through this together.

First, we need to calculate the inverse for each of the three matrices. The inverse of a rotation matrix R is equal to the rotation matrix’s transpose (RT = R-1), where T means “transpose” and -1 means “inverse”. If you don’t know how to take the transpose of a 3×3 matrix, take a look at this article.

And since the last operation performed is yaw, we need to take its transpose, then take the transpose of the pitch matrix, and then take the transpose of the roll matrix.

Here are the steps of the matrix multiplication:

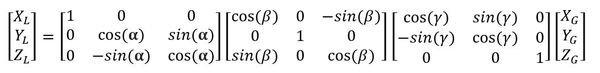
8-inverse-rotation-matrix
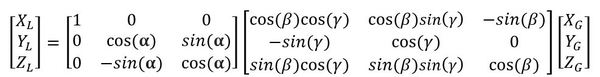
9-inverse-rotation-matrix
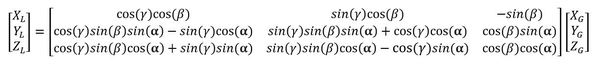
10-inverse-rotation-matrix

And there you have it. This matrix below is the full three-dimensional inverse rotation matrix. Use it when you want to convert a point (or vector) in the 3D global reference frame to a point (or vector) in the 3D local reference frame:

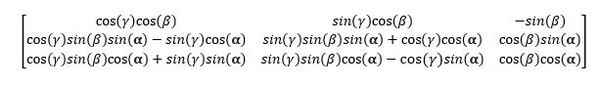
11-full-inverse-3d-rotation-matrix

Three-Dimensional Inverse Rotation Matrix in Python Code

Here is a NumPy-based method that converts angles into a 3×3 inverse rotation matrix like the one above. You can use this method in whatever code you want to write.

import numpy as np

def euler_rotation_matrix(alpha,beta,gamma):
    """
    Generate a full three-dimensional rotation matrix from euler angles

    Input
    :param alpha: The roll angle (radians) - Rotation around the x-axis
    :param beta: The pitch angle (radians) - Rotation around the y-axis
    :param alpha: The yaw angle (radians) - Rotation around the z-axis

    Output
    :return: A 3x3 element matix containing the rotation matrix. 
             This rotation matrix converts a point in the local reference 
             frame to a point in the global reference frame.

    """
    # First row of the rotation matrix
    r00 = np.cos(gamma) * np.cos(beta)
    r01 = np.cos(gamma) * np.sin(beta) * np.sin(alpha) - np.sin(gamma) * np.cos(alpha)
    r02 = np.cos(gamma) * np.sin(beta) * np.cos(alpha) + np.sin(gamma) * np.sin(alpha)
    
    # Second row of the rotation matrix
    r10 = np.sin(gamma) * np.cos(beta)
    r11 = np.sin(gamma) * np.sin(beta) * np.sin(alpha) + np.cos(gamma) * np.cos(alpha)
    r12 = np.sin(gamma) * np.sin(beta) * np.cos(alpha) - np.cos(gamma) * np.sin(alpha)
	
    # Third row of the rotation matrix
    r20 = -np.sin(beta)
    r21 = np.cos(beta) * np.sin(alpha)
    r22 = np.cos(beta) * np.cos(alpha)
	
    # 3x3 rotation matrix
    rot_matrix = np.array([[r00, r01, r02],
                           [r10, r11, r12],
                           [r20, r21, r22]])
						   
    return rot_matrix

def rotate(p1,alpha,beta,gamma):
    """
    Rotates a point p1 in 3D space in the local reference frame to 
    a point p2 in the global reference frame.

    Input
    :param p1: A 3 element array containing the position of a point in the 
              local reference frame (xL,yL,zL) 
    :param alpha: The roll angle (radians) - Rotation around the x-axis
    :param beta: The pitch angle (radians) - Rotation around the y-axis
    :param alpha: The yaw angle (radians) - Rotation around the z-axis

    Output
    :return: p2: A 3 element array containing the position of a point in the 
             global reference frame (xG,yG,zG)

    """
    p2 = euler_rotation_matrix(alpha, beta, gamma) @ p1
    return p2

def inverse_rotation(p2,alpha,beta,gamma):  
    """
    Inverse rotation from a point p2 in global 3D reference frame 
    to a point p1 in the local (robot) reference frame.

    Input
    :param p2: A 3 element array containing the position of a point in the 
               global reference frame (xG,yG,zG)
    :param alpha: The roll angle (radians) - Rotation around the x-axis
    :param beta: The pitch angle (radians) - Rotation around the y-axis
    :param alpha: The yaw angle (radians) - Rotation around the z-axis

    Output
    :return: A 3 element array containing the position of a point in the 
             local reference frame (xL,yL,zL) 

    """
    # First row of the inverse rotation matrix
    r00 = np.cos(gamma) * np.cos(beta)
    r01 = np.sin(gamma) * np.cos(beta)
    r02 = -np.sin(beta)
	
    # Second row of the inverse rotation matrix	
    r10 = np.cos(gamma) * np.sin(beta) * np.sin(alpha) - np.sin(gamma) * np.cos(alpha)
    r11 = np.sin(gamma) * np.sin(beta) * np.sin(alpha) + np.cos(gamma) * np.cos(alpha)	
    r12 = np.cos(beta) * np.sin(alpha)	
	
    # Third row of the inverse rotation matrix	
    r20 = np.cos(gamma) * np.sin(beta) * np.cos(alpha) + np.sin(gamma) * np.sin(alpha)
    r21 = np.sin(gamma) * np.sin(beta) * np.cos(alpha) - np.cos(gamma) * np.sin(alpha)
    r22 = np.cos(beta) * np.cos(alpha)
	
    # 3x3 inverse rotation matrix
    inv_rot_matrix = np.array([[r00, r01, r02],
                               [r10, r11, r12],
                               [r20, r21, r22]]) 
						   
    return inv_rot_matrix @ p2

def main():

    # Point that we want to rotate from local frame to global frame
    p1 = np.array([5,6,7])
    
    # Rotation angles
    alpha = (30/180.0)*np.pi
    beta =  (40/180.0)*np.pi
    gamma = (70/180.0)*np.pi

    print(f'local coordinates p1: {p1}')
    print(f'Rotated by Roll {alpha}, Pitch {beta}, Yaw: {gamma}')
    p2 = rotate(p1,alpha,beta,gamma)

    print(f'global coordinates p2:{p2}')
    p1_ = inverse_rotation(p2,alpha,beta,gamma)

    print(f'inverse rotation back into local frame p1:{p1_}')

if __name__ == '__main__':
    main()

Return to Table of Contents