How to Switch Between ROS 1 and ROS 2 in Ubuntu Linux

In this tutorial, I will show you how to switch between ROS 1 Noetic Ninjemys and ROS 2 Foxy Fitroy inside the same Ubuntu 20.04 system.

Prerequisites

You have Ubuntu Linux 20.04 installed and running properly.
You have ROS 1 Noetic installed and working properly.
You have ROS 2 Foxy Fitroy installed and working properly.

Switch From ROS 1 Noetic to ROS 2 Foxy Fitzroy

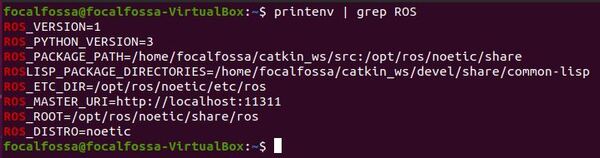
First let’s confirm what version of ROS we currently have active in our system.

Open a new terminal window, and type the following command:

printenv | grep ROS

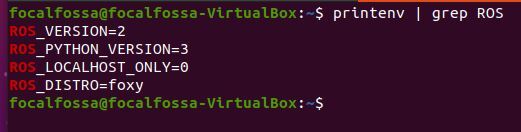
You can see that ROS 1 Noetic is the active ROS version right now.

Let’s switch to ROS 2 Foxy Fitzroy.

Open your bash file.

gedit ~/.bashrc

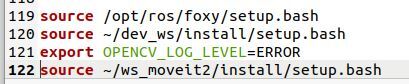
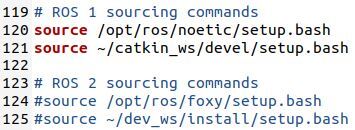
Scroll down to the bottom of your bash file, and you will see these lines.

Comment the lines out so they look like this.

Now, make sure you have the following lines so that we make ROS 2 Foxy the active ROS version. These lines can go below the ROS 1 sourcing commands.

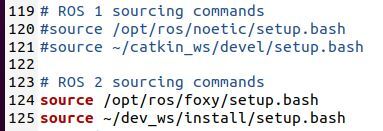
The two key lines that need to be uncommented are:

source /opt/ros/foxy/setup.bash
source ~/dev_ws/install/setup.bash

The name of the workspace for my ROS 2 work is dev_ws, but your workspace might be another name.

Save the file, and close it to go back to the terminal.

Open a new terminal window. Let’s see what the active ROS version is.

printenv | grep ROS

Switch From ROS 2 Foxy Fitzroy to ROS 1 Noetic

Now, let’s switch back from ROS 2 to ROS 1.

Uncomment the ROS 1 lines and comment out the ROS 2 lines.

gedit ~/.bashrc

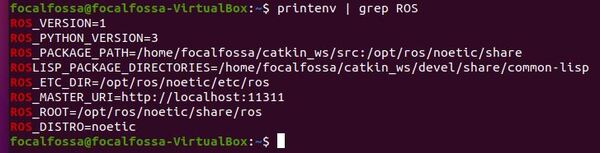
Open a new terminal window, and check what version of ROS is currently active in your system.

That’s it! Keep building!

How to Install MoveIt 2 for ROS 2 Foxy Fitzroy

In this tutorial, I will show you how to install MoveIt 2 for ROS 2 Foxy Fitzroy. MoveIt 2 is a popular software platform for controlling robotic arms (industrial, humanoid, and collaborative).

The official tutorial is located in the MoveIt 2 documentation, but we’ll run through the entire process step-by-step below.

You Will Need

In order to complete this tutorial, you will need:

ROS 2 Foxy Fitzroy installed on Ubuntu Linux 20.04

Update the Package List

The first thing you need to do is make sure you have the latest version of packages installed. Open a new terminal window, and type the following commands, one after the other.

sudo apt update

Upgrade any outdated packages

sudo apt dist-upgrade

Type Y, and then press Enter.

Update ROS dependencies.

rosdep update

Add Various ROS 2 Build Tools

Add some other build tools that Move It 2 needs. Copy and paste the full command below into your Linux terminal and then press Enter.

sudo apt install -y \
  build-essential \
  cmake \
  git \
  libbullet-dev \
  python3-colcon-common-extensions \
  python3-flake8 \
  python3-pip \
  python3-pytest-cov \
  python3-rosdep \
  python3-setuptools \
  python3-vcstool \
  wget \
  clang-format-10 && \
# install some pip packages needed for testing
python3 -m pip install -U \
  argcomplete \
  flake8-blind-except \
  flake8-builtins \
  flake8-class-newline \
  flake8-comprehensions \
  flake8-deprecated \
  flake8-docstrings \
  flake8-import-order \
  flake8-quotes \
  pytest-repeat \
  pytest-rerunfailures \
  pytest

Create a Workspace

Let’s create a workspace for our MoveIt 2 work. Open a new terminal, and type the following commands:

export COLCON_WS=~/ws_moveit2/

mkdir -p $COLCON_WS/src

cd $COLCON_WS/src

Download MoveIt 2

Download the MoveIt 2 repository.

wget https://raw.githubusercontent.com/ros-planning/moveit2/main/moveit2.repos

Now run this command. Be patient as it will take a while for this command to complete. Feel free to go get something to eat or drink.

vcs import < moveit2.repos

Make sure MoveIt 2 has all the dependencies it needs. This command below will also take several minutes to complete.

rosdep install -r --from-paths . --ignore-src --rosdistro foxy -y

Build MoveIt 2

Move to the root of the workspace.

cd $COLCON_WS

Build MoveIt 2. This command below will take a while to complete. Mine took 26 minutes and 51 seconds.

colcon build --event-handlers desktop_notification- status- --cmake-args -DCMAKE_BUILD_TYPE=Release

Here is what my terminal looks like after the build.

Source the Setup File for the Workspace

Open your .bashrc file, and add the following line to the very bottom of the file:

source ~/ws_moveit2/install/setup.bash

Test Your Installation

Open a new terminal window, and type the following commands to launch the demo.

cd ~/ws_moveit2

ros2 launch run_move_group run_move_group.launch.py

Here is another command you can run:

ros2 launch run_ompl_constrained_planning run_move_group.launch.py

Here is the output:

When you are finished, press CTRL + C in all terminal windows to shut everything down.

ROS 2 Tutorials – Foxy Fitzroy

In the tutorials below, you will get hands-on experience with the most important parts of ROS 2 Foxy Fitzroy, the latest distribution of ROS 2. I have hand picked the core areas of ROS 2 that you will use again and again in your robotics applications. This tutorial is designed to save you time and get you comfortable with ROS 2 as quickly as possible.

To get the most out of ROS 2, I recommend going through each of the tutorials below. Don’t worry if everything seems complicated and doesn’t make sense. Don’t worry if you can’t understand how any of these abstract concepts connect to a real-world robot.

ROS 2 is built in such a way that you need to work through the boring basics before you can use it to develop actual robotics projects. You have to walk before you learn how to run.

Without further ado, let’s get started!

Prerequisites

You understand how to create a simple “Hello World” program in C++.
You understand the basics of Python.
You understand the basics of Linux.

ROS 2 Foxy Fitzroy Tutorials

If you’ve made it through each of the tutorials above, congratulations! You now have a firm foundation in ROS 2 and can go out and confidently develop projects of your own or dive into an existing project.

Keep building!