In this tutorial, I’ll explain how PID (Proportional-Integral-Derivative) Control works using an analogy.
Imagine we are the captain of a ship. We want the boat to maintain a heading of due north automatically, without any human intervention.

We go out and hire a smart robotics software engineer to write a control algorithm for the ship.
The variable that we want to control is the ship’s heading, and we want to make sure the heading maintains a “set point” of due north (e.g. 0 degrees).
Proportional Control
- If the ship is heading slightly off course to the left, we want the ship to steer slightly to the right.
- If the ship is heading slightly off course to the right, we want the ship to steer slightly to the left.
- If the ship is heading strongly off course to the left, we want the ship to steer strongly to the right.
- If the ship is heading strongly off course to the right, we want the ship to steer strongly to the left.
In short, the steering magnitude is directly proportional to the difference between the desired heading and the current heading. The further you are off course, the harder the ship steers.
Mathematically, proportional control is:
Control Output = Kp * (Desired – Actual)
Where:
- Control Output is what you want to control (e.g. steering intensity, speed, etc.)
- Kp is some non-negative constant
- Desired = Set Point (e.g. the heading you want to achieve…i.e. 0 degrees north)
- Actual = Process Variable (e.g. the heading you measured)
- Error = Desired – Actual
The Proportional term is all about adjusting the output based on the present error.
Integral Control
Now let’s suppose that there is a crosswind. Even though the ship is adjusting the steering in proportion to the heading error, there are still differences between the actual and desired heading that are accumulating over time as a result of this ongoing crosswind.
The ship continues to drift off course even though proportional control is being applied.
The integral term looks for the residual error that is generated even after proportional control is applied. In this example, the residual error is caused by the wind, and it keeps adding up over time. The integral term seeks to get rid of this residual error by incorporating the historical cumulative value of the error. As the error decreases, the integral term will decrease.
Integral control looks for factors that keep pushing the ship off course and adjusts accordingly.
Mathematically, we now have to add the Integral term.
Control Output = Kp * Error + Ki * Sum of Errors Over Time
The Integral term is all about adjusting the output based on the past error.
Derivative Control
Let’s suppose that the ship is steering hard to the left in order to correct the heading. You don’t want the ship to steer so hard that momentum causes the ship to overshoot your desired heading.
What you want to do is have the ship slow down the steering as it approaches the heading.
The derivative term of PID control does this. It is used to slow down the heading correction as the measured heading approaches the desired heading. This derivative term helps the ship avoid overshooting.
Mathematically, we now have to add the Derivative term to get the final PID Control equation:
Control Output = Kp * Error + Ki * Sum of Errors Over Time + Kd * Rate of Change of the Error with Respect to Time
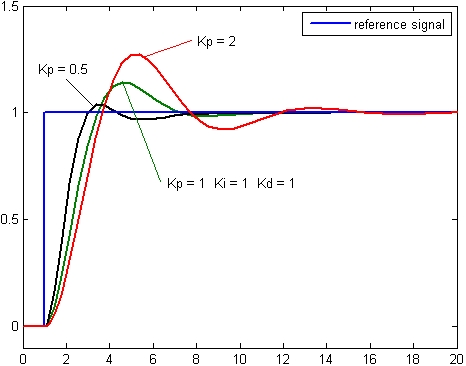
The Derivative term is all about adjusting the output based on the future (predicted) error. If the error is decreasing too quickly with respect to time, this term will reduce the control output.
Summary
PID is a control method that is made up of three terms:
- Proportional gain that scales the control output based on the difference between the actual state of the system and the desired state of the system (i.e. the error).
- Integral gain that scales the control output based on the accumulated error.
- Derivative gain that scales the control output based on the rate of change of the error (i.e. how fast the error is changing).



