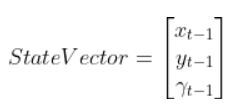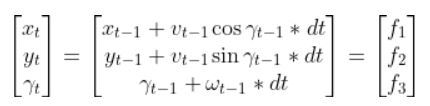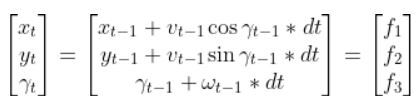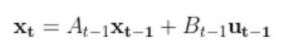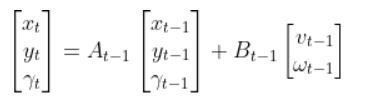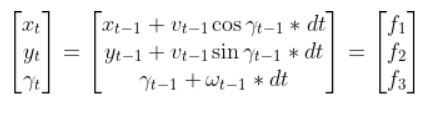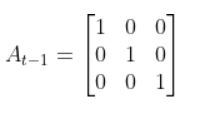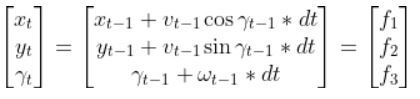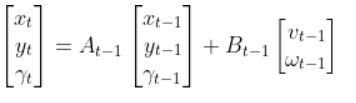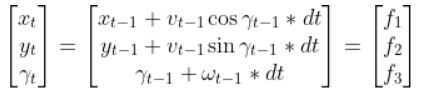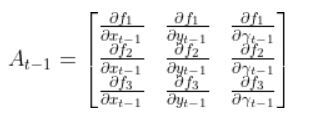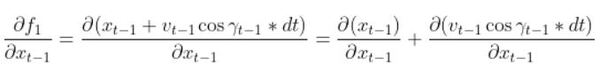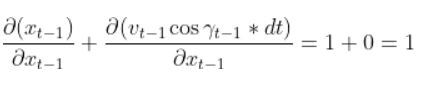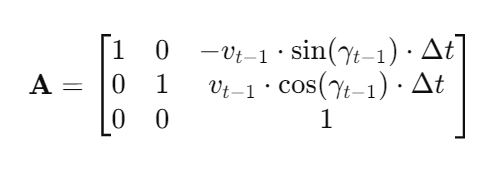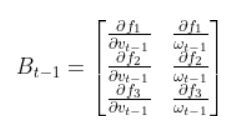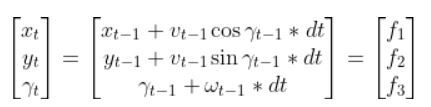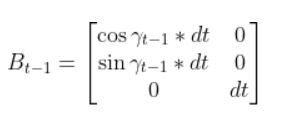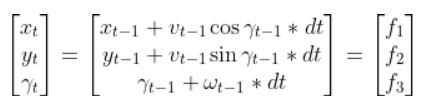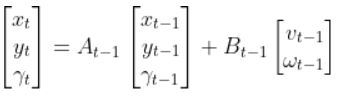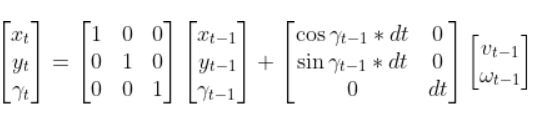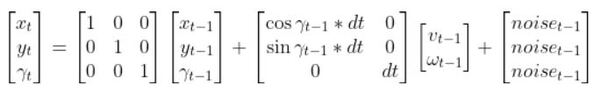In this tutorial, we will learn how to derive the observation model for a two-wheeled mobile robot (I’ll explain what an observation model is below). Specifically, we’ll assume that our mobile robot is a differential drive robot like the one on the cover photo. A differential drive robot is one in which each wheel is driven independently from the other.
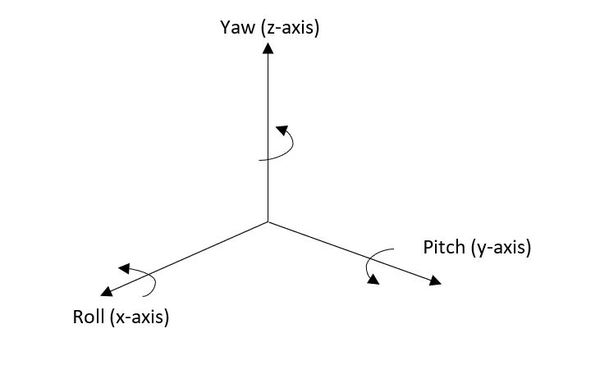
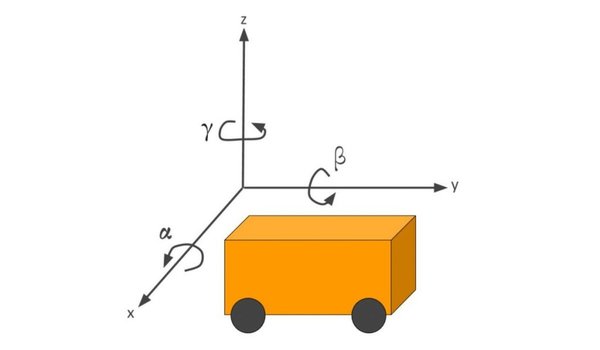
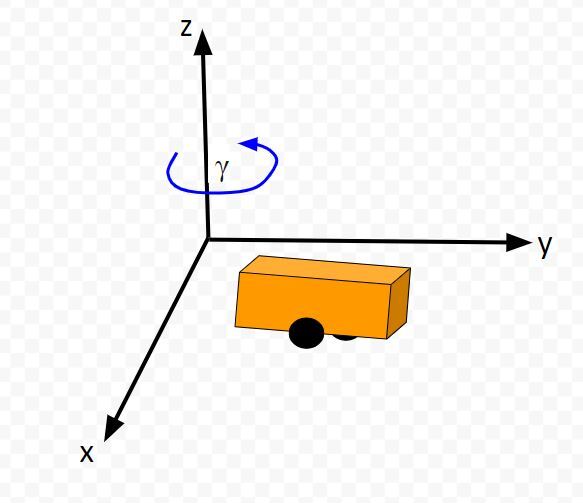
Below is a representation of a differential drive robot on a 3D coordinate plane with x, y, and z axes. The yaw angle γ represents the amount of rotation around the z axis as measured from the x axis.
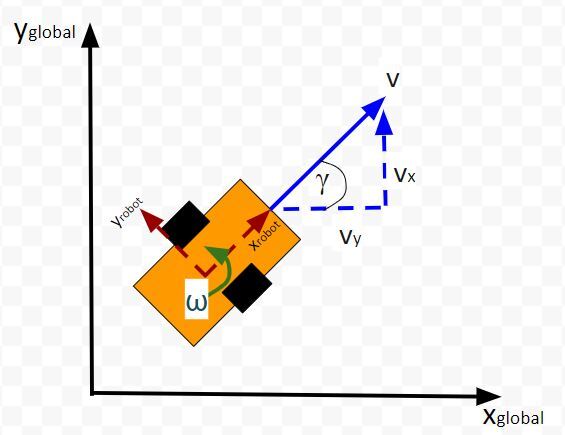
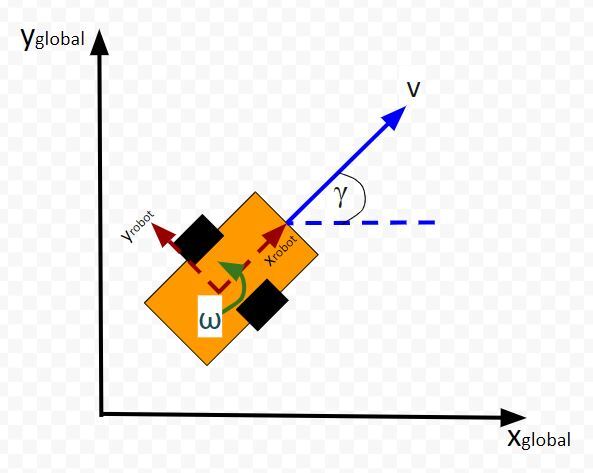
Here is the aerial view:
Real World Applications
- The most common application of deriving the observation model is when you want to do Kalman Filtering to smooth out noisy sensor measurements to generate a better estimate of the current state of a robotic system. I’ll cover this process in a future post. It is known as sensor fusion.
Prerequisites
- It is helpful if you have gone through my tutorial on state space modeling. Otherwise, if you understand the concept of state space modeling, jump right into this tutorial.
What is an Observation Model?
Typically, when a mobile robot is moving around in the world, we gather measurements from sensors to create an estimate of the state (i.e. where the robot is located in its environment and how it is oriented relative to some axis).
An observation model does the opposite. Instead of converting sensor measurements to estimate the state, we use the state (or predicted state at the next timestep) to estimate (or predict) sensor measurements. The observation model is the mathematical equation that does this calculation.
You can understand why doing something like this is useful. Imagine you have a state space model of your mobile robot. You want the robot to move from a starting location to a goal location. In order to reach the goal location, the robot needs to know where it is located and which direction it is moving.
Suppose the robot’s sensors are really noisy, and you don’t trust its observations entirely to give you an accurate estimate of the current state. Or perhaps, all of a sudden, the sensor breaks, or generates erroneous data.
The observation model can help us in these scenarios. It enables you to predict what the sensor measurements would be at some timestep in the future.
The observation model works by first using the state model to predict the state of the robot at that next timestep and then using that state prediction to infer what the sensor measurement would be at that point in time.
You can then compute a weighted average (i.e. this is what you do during Kalman Filtering) of the predicted sensor measurements and the actual sensor observation at that timestep to create a better estimate of your state.
This is what you do when you do Kalman Filtering. You combine noisy sensor observations with predicted sensor measurements (based on your state space model) to create a near-optimal estimate of the state of a mobile robot at some time t.
An observation model (also known as measurement model or sensor model) is a mathematical equation that represents a vector of predicted sensor measurements y at time t as a function of the state of a robotic system x at time t, plus some sensor noise (because sensors aren’t 100% perfect) at time t, denoted by vector wt.
Here is the formal equation:
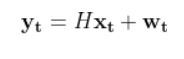
Because a mobile robot in 3D space has three states [x, y, yaw angle], in vector format, the observation model above becomes:
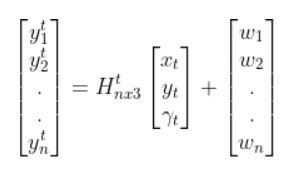
where:
- t = current time
- y vector (at left) = n predicted sensor observations at time t
- n = number of sensor observations (i.e. measurements) at time t
- H = measurement matrix (used to convert the state at time t into predicted sensor observations at time t) that has n rows and 3 columns (i.e. a column for each state variable).
- w = the noise of each of the n sensor observations (you often get this sensor error information from the datasheet that comes when you purchase a sensor)
Sensor observations can be anything from distance to a landmark, to GPS readings, to ultrasonic distance sensor readings, to odometry readings….pretty much any number you can read from a robotic sensor that can help give you an estimate of the robot’s state (position and orientation) in the world.
The reason why I say predicted measurements for the y vector is because they are not actual sensor measurements. Rather you are using the state of a mobile robot (i.e. the current location and orientation of a robot in 3D space) at time t-1 to predict the next state at time t, and then you use that next state (estimate) at time t to infer what the corresponding sensor measurement would be at that point in time t.
How to Calculate the H Matrix
Let’s examine how to calculate H. The measurement matrix H is used to convert the predicted state estimate at time t into predicted sensor measurements at time t.
Imagine you had a sensor that could measure the x position, y position, and yaw angle (i.e. rotation angle around the z-axis) directly. What would H be?
In this case, H will be the identity matrix since the estimated state maps directly to sensor measurements [x, y, yaw].
H has the same number of rows as sensor measurements and the same number of columns as states. Here is how the matrix would look in this scenario.
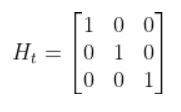
What if, for example, you had a landmark in your environment. How does the current state of the robot enable you to calculate the distance (i.e. range) to the landmark r and the bearing angle b to the landmark?
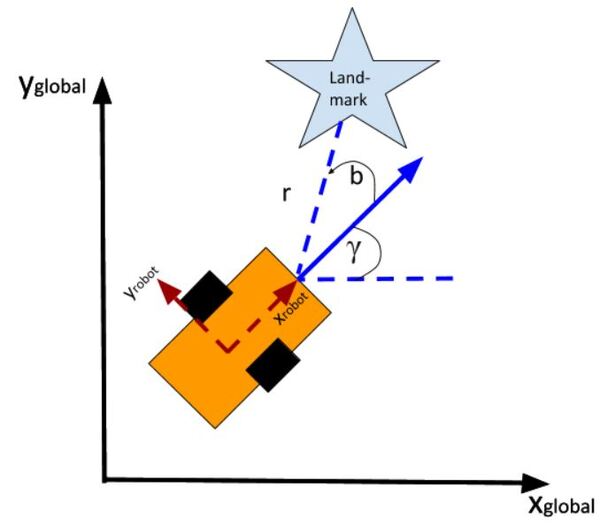
Using the Pythagorean Theorem and trigonometry, we get the following equations for the range r and bearing b:
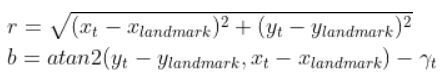
Let’s put this in matrix form.

The formulas in the vector above are nonlinear (note the arctan2 function). They enable us to take the current state of the robot at time t and infer the corresponding sensor observations r and b at time t.
Let’s linearize the model to create a linear observation model of the following form:
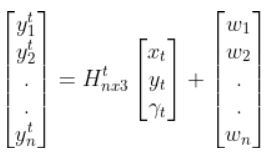
We have to calculate the Jacobian, just as we did when we calculated the A and B matrices in the state space modeling tutorial.
The formula for Ht is as follows:
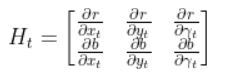
So we need to calculate 6 different partial derivatives. Here is what you should get:
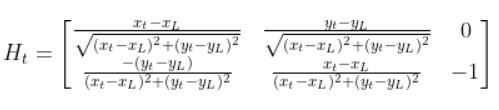
Putting It All Together
The final observation model is as follows:
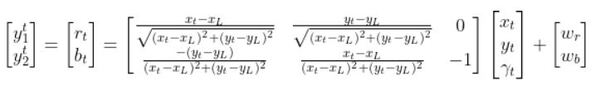
Equivalently, in some literature, you might see that all the stuff above is equal to:
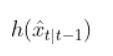
In fact, in the Wikipedia Extended Kalman Filter article, they replace time t with time k (not sure why because t is a lot more intuitive, but it is what it is).
Python Code Example for the Observation Model
Let’s create an observation model in code. As a reminder, here is our robot model (as seen from above).
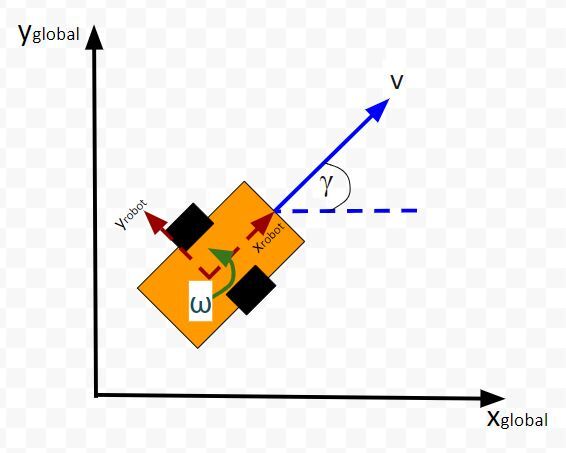
We’ll assume we have a sensor on our mobile robot that is able to give us exact measurements of the xglobal position in meters, yglobal position in meters, and yaw angle γ of the robot in radians at each timestep.
Therefore, as mentioned earlier,
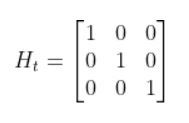
We’ll also assume that the corresponding noise (error) for our sensor readings is +/-0.07 m for the x position, +/-0.07 m for the y position, and +/-0.04 radians for the yaw angle. Therefore, here is the sensor noise vector:
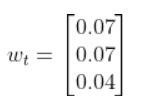
So, here is our equation:
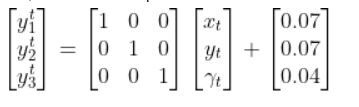
Suppose that the state of the robot at time t is [x=5.2, y=2.8, yaw angle=1.5708]. Because the yaw angle is 90 degrees (1.5708 radians), we know that the robot is heading due north relative to the global reference frame (i.e. the world or environment the robot is in).
What is the corresponding estimated sensor observation at time t given the current state of the robot at time t?
Here is the code:
import numpy as np
# Author: Addison Sears-Collins
# https://automaticaddison.com
# Description: An observation model for a differential drive mobile robot
# Measurement matrix H_t
# Used to convert the predicted state estimate at time t
# into predicted sensor measurements at time t.
# In this case, H will be the identity matrix since the
# estimated state maps directly to state measurements from the
# odometry data [x, y, yaw]
# H has the same number of rows as sensor measurements
# and same number of columns as states.
H_t = np.array([ [1.0, 0, 0],
[ 0,1.0, 0],
[ 0, 0, 1.0]])
# Sensor noise. This is a vector with the
# number of elements equal to the number of sensor measurements.
sensor_noise_w_t = np.array([0.07,0.07,0.04])
# The estimated state vector at time t in the global
# reference frame
# [x_t, y_t, yaw_t]
# [meters, meters, radians]
state_estimate_t = np.array([5.2,2.8,1.5708])
def main():
estimated_sensor_observation_y_t = H_t @ (
state_estimate_t) + (
sensor_noise_w_t)
print(f'State at time t: {state_estimate_t}')
print(f'Estimated sensor observations at time t: {estimated_sensor_observation_y_t}')
main()
Here is the output:

And that’s it folks. That linear observation model above enables you to convert the state at time t to estimated sensor observations at time t.
In a real robot application, we would use an Extended Kalman Filter to compute a weighted average of the estimated sensor reading using the observation model and the actual sensor reading that is mounted on your robot. In my next tutorial, I’ll show you how to implement an Extended Kalman Filter from scratch, building on the content we covered in this tutorial.
Keep building!