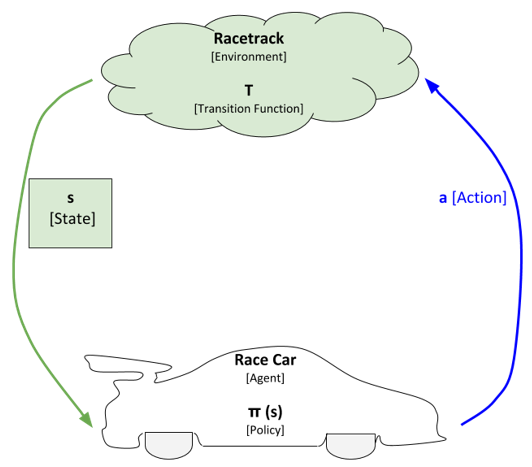
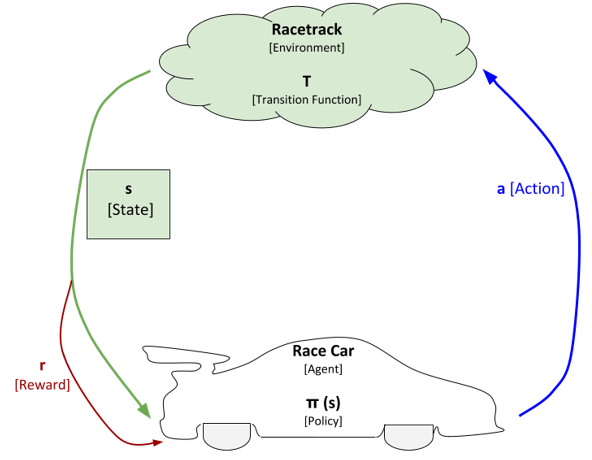
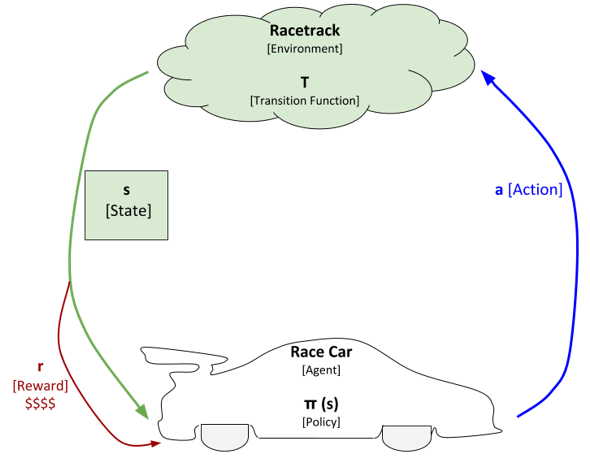
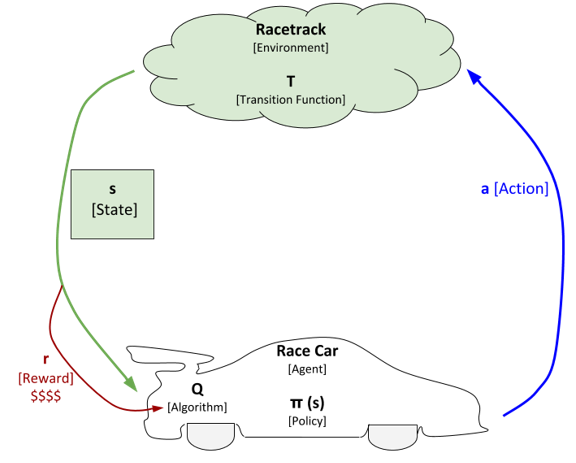
In this post, I will walk you through how to implement the value iteration and Q-learning reinforcement learning algorithms from scratch, step-by-step. We will not use any fancy machine learning libraries, only basic Python libraries like Pandas and Numpy.
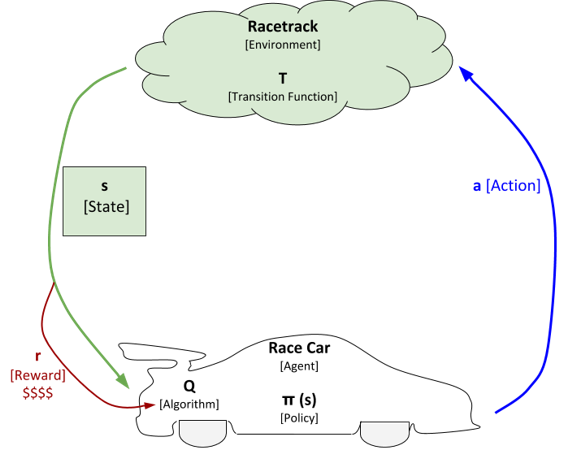
Our end goal is to implement and compare the performance of the value iteration and Q-learning reinforcement learning algorithms on the racetrack problem (Barto, Bradtke, & Singh, 1995).
In the racetrack problem, the goal is to control the movement of a race car along a predefined racetrack so that the race car travels from the starting position to the finish line in a minimum amount of time. The race car must stay on the racetrack and avoid crashing into walls along the way. The racetrack problem is analogous to a time trial rather than a competitive race since there are no other cars on the track to avoid.
Note: Before you deep dive into a section below, I recommend you check out my introduction to reinforcement learning post so you can familiarize yourself with what reinforcement learning is and how it works. Once you skim over that blog post, the rest of this article will make a lot more sense. If you are already familiar with how reinforcement learning works, no need to read that post. Just keep reading this one.
Without further ado, let’s get started!
Table of Contents
- Testable Hypotheses
- How Value Iteration Works
- How Q-Learning Works
- Experimental Design and Tuning Process
- Input Files
- Value Iteration Code in Python
- Q-Learning Code in Python
- Experimental Output and Analysis
- Video Demonstration
Testable Hypotheses
The two reinforcement learning algorithms implemented in this project were value iteration and Q-learning. Both algorithms were tested on two different racetracks: an R-shaped racetrack and an L-shaped racetrack. The number of timesteps the race car needed to take from the starting position to the finish line was calculated for each algorithm-racetrack combination.
Using the implementations of value iteration and Q-learning, three hypotheses will be tested.
Hypothesis 1: Both Algorithms Will Enable the Car to Finish the Race
I hypothesize that value iteration and Q-learning will both generate policies that will enable the race car to successfully finish the race on all racetracks tested (i.e. move from the starting position of the racetracks to the finish line).
Hypothesis 2: Value Iteration Will Learn Faster Than Q-Learning
I hypothesize that value iteration will generate a learning policy faster than Q-learning because it has access to the transition and reward functions (explained in detail in the next section “Algorithms Implemented”).
Hypothesis 3: Bad Crash Version 1 Will Outperform Bad Crash Version 2
I hypothesize that it will take longer for the car to finish the race for the crash scenario in which the race car needs to return to the original starting position each time it crashes into a wall. In other words, Bad Crash Version 1 (return to nearest open position) performance will be better than Bad Crash Version 2 (return to start) performance.
How Value Iteration Works
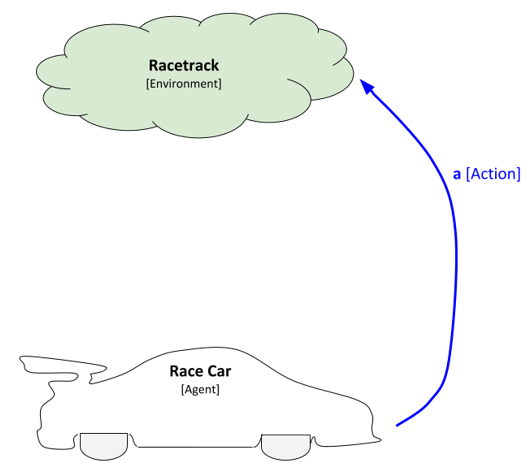
In the case of the value iteration reinforcement learning algorithm, the race car (i.e. agent) knows two things before taking a specific action (i.e. accelerate in x and/or y directions) (Alpaydin, 2014):
- The probabilities of ending up in other new states given a particular action is taken from a current state.
- More formally, the race car knows the transition function.
- As discussed in the previous section, the transition function takes as input the current state s and selected action a and outputs the probability of transitioning to some new state s’.
- The immediate reward (e.g. race car gets -1 reward each time it moves to a new state) that would be received for taking a particular action from a current state.
- More formally, this is known as the reward function.
- The reward function takes as input the current state s and selected action a and outputs the reward.
Value iteration is known as a model-based reinforcement learning technique because it tries to learn a model of the environment where the model has two components:
- Transition Function
- The race car looks at each time it was in a particular state s and took a particular action a and ended up in a new state s’. It then updates the transition function (i.e. transition probabilities) according to these frequency counts.
- Reward Function
- This function answers the question: “Each time the race car was in a particular state s and took a particular action a, what was the reward?”
In short, in value iteration, the race car knows the transition probabilities and reward function (i.e. the model of the environment) and uses that information to govern how the race car should act when in a particular state. Being able to look ahead and calculate the expected rewards of a potential action gives value iteration a distinct advantage over other reinforcement learning algorithms when the set of states is small in size.
Let us take a look at an example. Suppose the following:
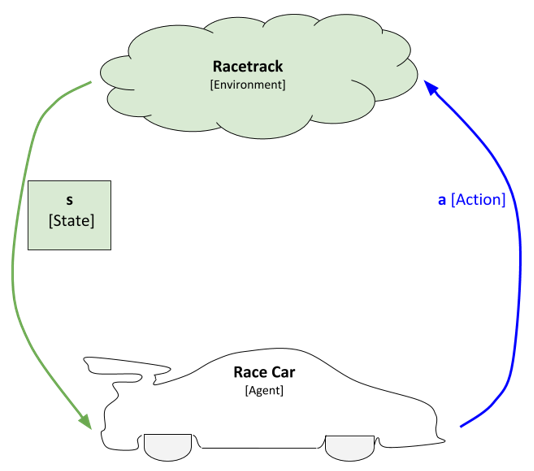
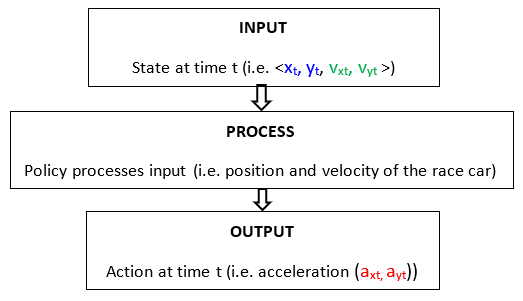
- The race car is in state so, where s0 = <x0, y0, vx0, vy0>, corresponding to the x-position on a racetrack, y-position on a race track, velocity in the x direction, and velocity in the y direction, at timestep 0.
- The race car takes action a0, where a0 = (ax0, ay0) = (change in velocity in x-direction, change in velocity in y-direction)
- The race car then observes the new state, where the new state is s1, where s1 = <x1, y1, vx1, vy1>.
- The race car receives a reward r0 for taking action a0 in state s0.
Putting the bold-faced variables together, we get the following expression which is known as an experience tuple. Tuples are just like lists except the data inside of them cannot be changed.
Experience Tuple = <s0, a0, s1, r0>
What the experience tuple above says is that if the race car is in state s0 and takes action a0, the race car will observe a new state s1 and will receive reward r0.
Then at the next time step, we generate another experience tuple that is represented as follows.
Experience Tuple = <s1, a1, s2, r1>
This process of collecting experience tuples as the race car explores the race track (i.e. environment) happens repeatedly.
Because value iteration is a model based approach, it builds a model of the transition function T[s, a, s’] and reward function R[s,a,s’] using the experience tuples.
- The transition function can be built and updated by adding up how many times the race car was in state s and took a particular action a and then observed a new state s’. Recall that T[s, a, s’] stands for the probability the race car finds itself in a new state s’ (at the next timestep) given that it was in state s and took action a.
- The reward function can be built by examining how many times the race car was in state s and took a particular action a and received a reward r. From that information the average reward for that particular scenario can be calculated.
Once these models are built, the race car can then can use value iteration to determine the optimal values of each state (hence the name value iteration). In some texts, values are referred to as utilities (Russell, Norvig, & Davis, 2010).
What are optimal values?
Each state s in the environment (denoted as <xt, yt, vxt, vyt > in this racetrack project) has a value V(s). Different actions can be taken in a given state s. The optimal values of each state s are based on the action a that generates the best expected cumulative reward.
Expected cumulative reward is defined as the immediate reward that the race car would receive if it takes action a and ends up in the state s + the discounted reward that the race car would receive if it always chose the best action (the one that maximizes total reward) from that state onward to the terminal state (i.e. the finish line of the racetrack).
V*(s) = best possible (immediate reward + discounted future reward)
where the * means “optimal.”
The reason why those future rewards are discounted (typically by a number in the range [0,1), known as gamma γ) is because rewards received far into the future are worth less than rewards received immediately. For all we know, the race car might have a gas-powered engine, and there is always the risk of running out of gas. After all, would you rather receive $10 today or $10 ten years from now? $10 received today is worth more (e.g. you can invest it to generate even more cash). Future rewards are more uncertain so that is why we incorporate the discount rate γ.
It is common in control applications to see state-action pairs denoted as Q*(s, a) instead of V*(s) (Alpaydin, 2014). Q*(s,a) is the [optimal] expected cumulative reward when the race car takes an action a in state s and always takes the best action after that timestep. All of these values are typically stored in a table. The table maps state-action pairs to the optimal Q-values (i.e. Q*(s,a)).
Each row in the table corresponds to a state-action-value combination. So in this racetrack problem, we have the following entries into the value table:
[x, y, vx, vy, ax, ay, Q(s,a)] = [x-coordinate, y-coordinate, velocity in x-direction, velocity in y-direction, acceleration in x-direction, acceleration in y-direction, value when taking that action in that state]
Note that Q(s,a) above is not labeled Q*(s,a). Only once value iteration is done can we label it Q*(s,a) because it takes time to find the optimal Q values for each state-action pair.
With the optimal Q values for each state-action pair, the race car can calculate the best action to take given a state. The best action to take given a state is the one with the highest Q value.
At this stage, the race car is ready to start the engine and leave the starting position.
At each timestep of the race, the race car observes the state (i.e. position and velocity) and decides what action to apply by looking at the value table. It finds the action that corresponds to the highest Q value for that state. The car then takes that action.
The pseudocode for calculating the optimal value for each state-action pair (denoted as Q*(s,a)) in the environment is below. This algorithm is the value iteration algorithm because it iterates over all the state-action pairs in the environment and gives them a value based on the cumulative expected reward of that state-action pair (Alpaydin, 2014; Russell, Norvig, & Davis, 2010; Sutton & Barto, 2018):
Value Iteration Algorithm Pseudocode
Inputs
- States:
- List of all possible values of x
- List of all possible values of y
- List of all possible values of vx
- List of all possible values of vy
- Actions:
- List of all the possible values of ax
- List of all possible values of ay
- Model:
- Model = Transition Model T[s, a, s’] + Reward Model R[s, a, s’]
- Where Model is a single table with the following row entries
- [s, a, s’, probability of ending up in a new state s’ given state s and action a, immediate reward for ending up in new state s’ given state s and action a]
- = [s, a, s’, T(s, a, s’), R(s, a, s’)]
- Note that the reward will be -1 for each state except the finish line states (i.e. absorbing or terminal states), which will have a reward of 0.
- Discount Rate:
- γ
- Where 0 ≤ γ < 1
- If γ = 0, rewards received immediately are the only thing that counts.
- As γ gets close to 1, rewards received further in the future count more.
- γ
- Error Threshold
- Ɵ
- Ɵ is a small number that helps us to determine when we have optimal values for each state-action pair (also known as convergence).
- Ɵ helps us know when the values of each state-action pair, denoted as Q(s,a), stabilize (i.e. stop changing a lot from run to run of the loop).
- Ɵ
Process
- Create a table V(s) that will store the optimal Q-value for each state. This table will help us determine when we should stop the algorithm and return the output. Initialize all the values of V(s) to arbitrary values, except the terminal state (i.e. finish line state) that has a value of 0.
- Initialize all Q(s,a) to arbitrary values, except the terminal state (i.e. finish line states) that has a value of 0.
- Initialize a Boolean variable called done that is a flag to indicate when we are done building the model (or set a fixed number of training iterations using a for loop).
- While (Not Done)
- Initialize a value called Δ to 0. When this value gets below the error threshold Ɵ, we exit the main loop and return the output.
- For all possible states of the environment
- v := V(s) // Extract and store the most recent value of the state
- For all possible actions the race car (agent)
can take
- Q(s,a) = (expected immediate reward given the state s and an action a) + (discount rate) * [summation_over_all_new_states(probability of ending up in a new state s’given a state s and action a * value of the new state s’)]
- More formally,
- where = expected immediate return when taking action a from state s
- V(s) := maximum value of Q(s,a) across all the different actions that the race car can take from state s
- Δ := maximum(Δ, |v – V(s)|)
- Is Δ < Ɵ? If yes, we are done (because the values of V(s) have converged i.e. stabilized), otherwise we are not done.
Output
The output of the value iteration algorithm is the value table, the table that maps state-action pairs to the optimal Q-values (i.e. Q*(s,a)).
Each row in the table corresponds to a state-action-value combination. So in this racetrack problem, we have the following entries into the value table:
[x, y, vx, vy, ax, ay, Q(s,a)] = [x-coordinate, y-coordinate, velocity in x-direction, velocity in y-direction, acceleration in x-direction, acceleration in y-direction, value when taking that action in that state]
Policy Determination
With the optimal Q values for each state-action pair, the race car can calculate the best action to take given a state. The best action to take given a state is the one with the highest Q value.
At this stage, the race car is ready to start the engine and leave the starting position.
At each timestep t of the race, the race car observes the state st (i.e. position and velocity) and decides what action at to apply by looking at the value table. It finds the action that corresponds to the highest Q value for that state (the action that will generate the highest expected cumulative reward). The car then takes that action at*, where at* means the optimal action to take at time t.
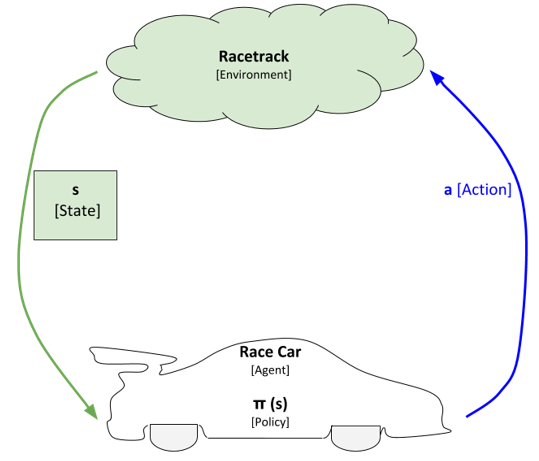
More formally, the optimal policy for a given states s at timestep t is π*(s) where:
For each state s do
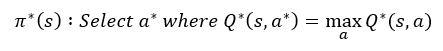
Value Iteration Summary
So, to sum up, on a high level, the complete implementation of an autonomous race car using value iteration has two main steps:
- Step 1: During the training phase, calculate the value of each state-action pair.
- Step 2: At each timestep of the time trial, given a current state s, select the action a where the state-action pair value (i.e. Q*(s,a)) is the highest.
How Q-Learning Works
Overview
In most real-world cases, it is not computationally efficient to build a complete model (i.e. transition and reward function) of the environment beforehand. In these cases, the transition and reward functions are unknown. To solve this issue, model-free reinforcement learning algorithms like Q-learning were invented (Sutton & Barto, 2018) .
In the case of model-free learning, the race car (i.e. agent) has to interact with the environment and learn through trial-and-error. It cannot look ahead to inspect what the value would be if it were to take a particular action from some state. Instead, in Q-learning, the race car builds a table of Q-values denoted as Q(s,a) as it takes an action a from a state s and then receives a reward r. The race car uses the Q-table at each timestep to determine the best action to take given what it has learned in previous timesteps.
One can consider Q[s,a] as a two-dimensional table that has the states s as the rows and the available actions a as the columns. The value in each cell of this table (i.e. the Q-value) represents the value of taking action a in state s.
Just like in value iteration, value has two components, the immediate reward and the discounted future reward.
More formally,
Q[s,a] = immediate reward + discounted future reward
Where immediate reward is the reward you get when taking action a from state s, and discounted future reward is the reward you get for taking actions in the future, discounted by some discount rate γ. The reason why future rewards are discounted is because rewards received immediately are more certain than rewards received far into the future (e.g. $1 received today is worth more than $1 received fifty years from now).
So, how does the race car use the table Q[s,a] to determine what action to take at each timestep of the time trial (i.e. what is the policy given a state…π(s))?
Each time the race car observes state s, it consults the Q[s,a] table. It takes a look to see which action generated the highest Q value given that observed state s. That action is the one that it takes.
More formally,
π(s) = argmaxa(Q[s,a])
argmax is a function that returns the action a that maximizes the expression Q[s,a]. In other words, the race car looks across all position actions given a state and selects the action that has the highest Q-value.
After Q-learning is run a number of times, an optimal policy will eventually be found. The optimal policy is denoted as π*(s). Similarly the optimal Q-value is Q*[s,a].
How the Q[s,a] Table Is Built
Building the Q[s,a] table can be broken down into the following steps:
- Choose the environment we want to train on.
- In this race car problem, the racetrack environment is what we want the race car to explore and train on.
- The racetrack provides the x and y position data that constitutes a portion of the state s that will be observed at each timestep by the racecar (agent).
- Starting from the starting position, the race car moves through the environment, observing the state s at a given timestep
- The race car consults the policy π(s), the function that takes as input the current state and outputs an action a.
- The action a taken by the race car changes the state of the environment from s to s’. The environment also generates a reward r that is passed to the race car.
- Steps 2-4 generate a complete experience tuple (i.e. a tuple is a list that does not change) of the form <s, a, s’, r> = <state, action, new state, reward>.
- The experience tuple in 5 is used to update the Q[s,a] table.
- Repeat steps 3-6 above until the race car gets to the terminal state (i.e. the finish line of the racetrack).
With the Q[s,a] table built, the race car can now test the policy. Testing the policy means starting at the starting position and consulting the Q[s,a] table at each timestep all the way until the race car reaches the finish line. We count how many timesteps it took for the race car to reach the finish line. If the time it took the race car to complete the time trial is not improving, we are done. Otherwise, we make the race car go back through the training process and test its policy again with an updated Q[s,a] table.
We expect that eventually, the performance of the race car will reach a plateau.
How the Q[s,a] Table Is Updated
With those high level steps, let us take a closer look now at how the Q[s,a] table is updated in step 6 in the previous section.
Each time the race car takes an action, the environment transitions to a new state s’ and gives the race car a reward r. This information is used by the race car to update its Q[s,a] table.
The update rule consists of two parts, where Q’[s,a] is the new updated Q-value for an action a taken at state s.
Q’[s,a] = Q[s,a] + α * (improved estimate of Q[s,a] – Q[s,a])
where α is the learning rate.
The learning rate is a number 0 < α ≤ 1 (commonly 0.2). Thus, the new updated Q-value is a blend of the old Q-value and the improved estimate of the Q value for a given state-action pair. The higher the learning rate, the more new information is considered when updating the Q-value. A learning rate of 1 means that the new updated Q-value is only considering the new information.
The equation above needs to be expanded further.
Q’[s,a] =Q[s,a] + α*(immediate reward + discounted future reward – Q[s,a])
Q’[s,a] = Q[s,a] + α * (r + γ * future reward – Q[s,a])
Where γ is the discount rate. It is typically by a number in the range [0,1). It means that rewards received by the race car (agent) in the far future are worth less than an immediate reward.
Continuing with the expansion of the equation, we have:
Q’[s,a] = Q[s,a] + α * (r + γ * Q[s’, optimal action a’ at new state s’] – Q[s,a])
Note in the above equation that we assume that the race car reaches state s’ and takes the best action from there, where best action is the action a’ that has the highest Q-value for that given new state s’.
More formally the update rule is as follows:
Q’[s,a] = Q[s,a] + α * (r + γ * Q[s’, argmaxa’(Q[s’,a’])] – Q[s,a])
Where argmaxa’(Q[s’,a’]) returns the action a’ that has the highest Q value for a given state s’.
How an Action Is Selected at Each Step
The performance of Q-learning is improved the more the race car explores different states and takes different actions in those states. In other words, the more state-action pairs the race car explores, the better Q[s,a] table the race car is able to build.
One strategy for forcing the race car to explore as much of the state-action space as possible is to add randomness into the Q-learning procedure. This is called exploration. More specifically, at the step of Q-learning where the race car selects an action based on the Q[s,a] table:
- There is a 20% chance ε that the race car will do some random action, and a 80% chance the race car will do the action with the highest Q-value (as determined by the Q[s,a] table). The latter is known as exploitation.
- If the race car does some random action, the action is chosen randomly from the set of possible actions the race car can perform.
I chose 20% as the starting probability (i.e. ε) of doing some random action, but it could be another number (e.g. 30%) As the race car gains more experience and the Q[s,a] table gets better and better, we want the race car to take fewer random actions and follow its policy more often. For this reason, it is common to reduce ε with each successive iteration, until we get to a point where the race car stops exploring random actions.
Q-Learning Algorithm Pseudocode
Below are is the Q-learning algorithm pseudocode on a high level (Alpaydin, 2014; Sutton & Barto, 2018).
Inputs
- Learning rate α, where 0 < α ≤ 1 (e.g. 0.2)
- Discount rate γ (e.g. 0.9)
- Exploration probability ε, corresponding to the probability that the race car will take a random action given a state (e.g. 0.2)
- Reduction of exploration probability, corresponding to how much we want to decrease ε at each training iteration (defined as a complete trip from the starting position to the finish line terminal state) of the Q-learning process. (e.g. 0.5)
- Number of training iterations (e.g. 1,000,000)
- States:
- List of all possible values of x
- List of all possible values of y
- List of all possible values of vx
- List of all possible values of vy
- Actions:
- List of all the possible values of ax
- List of all possible values of ay
Process
- Initialize the Q[s,a] table to small random values, except for the terminal state which will have a value of 0.
- For a fixed number of training iterations
- Initialize the state to the starting position of the race track
- Initialize a Boolean variable to see if the race car has crossed the finish line (i.e. reached the terminal state)
- While the race car has not reached the finish
line
- Select the action a using the Q[s,a] table that corresponds to the highest Q value given state s
- Take action a
- Observe the reward r and the new state s’
- Update the Q[s,a] table:
- Q[s,a] := Q[s,a] + α * (r + γ * Q[s’, argmaxa’(Q[s’,a’])] – Q[s,a])
- s := s’
- Check if we have crossed the finish line
Output
Algorithm returns the Q[s,a] table which is used to determine the optimal policy.
Policy Determination
Each time the race car observes state s, it consults the Q[s,a] table. It takes a look to see which action generated the highest Q value given that observed state s. That action is the one that it takes.
More formally,
π(s) = argmaxa(Q[s,a])
argmax is a function that returns the action a that maximizes the expression Q[s,a]. In other words, the race car looks across all position actions given a state and selects the action that has the highest Q-value.
Helpful Video
Here is a good video where Professor Tucker Balch from Georgia Tech goes through Q-learning, step-by-step:
Experimental Design and Tuning Process
Experimental Design
The Q-learning and value iteration algorithms were implemented for the racetrack problem and then tested on two different racetracks: an R-shaped racetrack and an L-shaped racetrack. The number of timesteps the race car needed to find the finish line was calculated for each algorithm-racetrack combination. The number of training iterations was also monitored. 10 experiments for each algorithm-racetrack combination were performed to create data to graph a learning curve.
At each timestep t of the racetrack problem, we have the following variables (below). We assume the racetrack is a Cartesian grid with an x-axis and a y-axis, and that the system is governed by the standard laws of kinematics:
- State = <xt, yt,
vxt, vyt> = variables that describe the current
situation (i.e. environment)
- xt = x coordinate of the location of the car at timestep t
- yt = y coordinate of the location of the car at timestep t
- vxt = velocity in the x direction at
time step t, where vxt = xt – xt-1
- Maximum vxt = 5
- Minimum vxt = -5
- vyt = velocity in the y direction at timestep t, where vyt = yt – yt-1
- Action = <axt, ayt>
= control variables = what the race car (i.e. agent) can do to influence the
state
- axt = accelerate in the x direction
at timestep t, where axt = vxt – vx t-1
- -1 (decrease velocity in x-direction by 1)
- 0 (keep same velocity), or
- 1 (increase velocity in x-direction by 1)
- ayt = acceleration in the y direction
at timestep t, where ayt = vyt – vy t-1
- -1 (decrease velocity in y-direction by 1)
- 0 (keep same velocity)
- 1 (increase velocity in y-direction by 1)
- axt = accelerate in the x direction
at timestep t, where axt = vxt – vx t-1
Example Calculation
At t = 0, the race car observes the current state. Location is (2,2) and velocity is (1,0).
- State = <xt, yt, vxt, vyt> = <x0, y0, vx0, vy0> = <2, 2, 1, 0>
- This means the race car is moving east one grid square per timestep because the x-component of the velocity is 1, and the y-component is 0.
After observing the state, the race car selects an action. It accelerates with acceleration (1,1).
- Action=(ax0, ay0)=(1, 1) = (increase velocity in x-direction by 1, increase velocity in y-direction by 1)
At t = 1, the race car observes the state.
- Velocity is now (vx0 + ax0, vy0 + ay0) = (1 + 1, 0 + 1) = (vx1, vy1) = (2, 1)
- Position (i.e. x and y coordinates) is now (x0 + vx1, y0 + vy1) = (2 + 2, 2 + 1) = (x1, y1) = (4, 3)
- Thus, putting it all together, the new state is now <x1, y1, vx1, vy1> = <4, 3, 2, 1>
Acceleration is Not Guaranteed
There is another twist with the racetrack problem. At any timestep t, when the race car attempts to accelerate, there is a 20% chance that the attempt will fail. In other words, each time the race car selects an action, there is a:
- 20% chance that the attempt fails, and velocity remains unchanged at the next timestep; i.e. (axt, ayt) = (0, 0)
- 80% chance velocity changes at the next timestep; (axt, ayt) = (selected acceleration in the x-direction, selected acceleration in y-direction)
Must Avoid Crashing Into Walls
The race car must stay on the track. Crashing into walls is bad. Two versions of a “bad crash” will be implemented in this project:
- Bad Crash Version 1: If the car crashes
into a wall,
- The car is placed at the nearest position on the track to the place where the car crashed.
- The velocity is set to (0, 0).
- Bad Crash Version 2: If the car crashes
into a wall,
- The car must go back to the original starting position.
- The velocity is set to (0, 0).
In this project, the performance of both versions of bad crash will be compared side by side for the reinforcement learning algorithms implemented in this project.
Reward Function
Because the goal is for the race car to go from the starting position to the finish line in the minimum number of timesteps, we assign a reward of -1 for each move the car makes. Because the reward is negative, this means that the race car incurs a cost (i.e. penalty) of 1 each time the race car moves to another position. The goal is to get to the finish line in as few moves (i.e. time steps) as possible in order to minimize the total cost (i.e. maximize the total reward).
The finish line is the final state (often referred to as terminal or absorbing state). This state has a reward of 0. There is no requirement to stop right on the finish position (i.e. finish line). It is sufficient to cross it.
Description of Any Tuning Process Applied
In order to compare the performance of the algorithm for the different crash scenarios, the principal hyperparameters were kept the same for all runs. These hyperparameters are listed below.
Learning Rate
The Learning rate α was set to 0.2.
Discount Rate
The discount rate γ was set to 0.9.
Exploration Probability
The exploration probability ε was set to 0.2 as dictated by the problem statement.
Number of Training Iterations
The number of training iterations was varied in order to computer the learning curve (see Results section below)
Input Files
Here are the tracks used in this project (S= Starting States; F = Finish States, # = Wall, . = Track):
Value Iteration Code in Python
Here is the full code for value iteration. Don’t be scared by how long this code is. I included a lot of comments so that you know what is going on at each step of the code. This and the racetrack text files above are all you need to run the program (just copy and paste into your favorite IDE!):
import os # Library enables the use of operating system dependent functionality
import time # Library handles time-related tasks
from random import shuffle # Import shuffle() method from the random module
from random import random # Import random() method from the random module
from copy import deepcopy # Enable deep copying
import numpy as np # Import Numpy library
# File name: value_iteration.py
# Author: Addison Sears-Collins
# Date created: 8/14/2019
# Python version: 3.7
# Description: Implementation of the value iteration reinforcement learning
# algorithm for the racetrack problem.
# The racetrack problem is described in full detail in:
# Barto, A. G., Bradtke, S. J., Singh, S. P. (1995). Learning to Act Using
# Real-time Dynamic Programming. Artificial Intelligence, 72(1-2):81–138.
# and
# Sutton, Richard S., and Andrew G. Barto. Reinforcement learning :
# An Introduction. Cambridge, Massachusetts: The MIT Press, 2018. Print.
# (modified version of Exercise 5.12 on pg. 111)
# Define constants
ALGORITHM_NAME = "Value_Iteration"
FILENAME = "R-track.txt"
THIS_TRACK = "R_track"
START = 'S'
GOAL = 'F'
WALL = '#'
TRACK = '.'
MAX_VELOCITY = 5
MIN_VELOCITY = -5
DISC_RATE = 0.9 # Discount rate, also known as gamma. Determines by how much
# we discount the value of a future state s'
ERROR_THRES = 0.001 # Determine when Q-values stabilize (i.e.theta)
PROB_ACCELER_FAILURE = 0.20 # Probability car will try to take action a
# according to policy pi(s) = a and fail.
PROB_ACCELER_SUCCESS = 1 - PROB_ACCELER_FAILURE
NO_TRAINING_ITERATIONS = 10 # A single training iteration runs through all
# possible states s
NO_RACES = 10 # How many times the race car does a single time trial from
# starting position to the finish line
FRAME_TIME = 0.3 # How many seconds between frames printed to the console
MAX_STEPS = 500 # Maximum number of steps the car can take during time trial
MAX_TRAIN_ITER = 50 # Maximum number of training iterations
# Range of the velocity of the race car in both y and x directions
vel_range = range(MIN_VELOCITY, MAX_VELOCITY + 1)
# All actions A the race car can take
# (acceleration in y direction, acceleration in x direction)
actions = [(-1,-1), (0,-1), (1,-1),
(-1,0) , (0,0), (1,0),
(-1,1) , (0,1), (1,1)]
def read_environment(filename):
"""
This method reads in the environment (i.e. racetrack)
:param str filename
:return environment: list of lists
:rtype list
"""
# Open the file named filename in READ mode.
# Make the file an object named 'file'
with open(filename, 'r') as file:
# Read until end of file using readline()
# readline() then returns a list of the lines
# of the input file
environment_data = file.readlines()
# Close the file
file.close()
# Initialize an empty list
environment = []
# Adds a counter to each line in the environment_data list,
# i is the index of each line and line is the actual contents.
# enumerate() helps get not only the line of the environment but also
# the index of that line (i.e. row)
for i,line in enumerate(environment_data):
# Ignore the first line that contains the dimensions of the racetrack
if i > 0:
# Remove leading or trailing whitespace if applicable
line = line.strip()
# If the line is empty, ignore it
if line == "": continue
# Creates a list of lines. Within each line is a list of
# individual characters
# The stuff inside append(stuff) first creates a new_list = []
# It then appends all the values in a given line to that new
# list (e.g. new_list.append(all values inside the line))
# Then we append that new list to the environment list.
# Therefoer, environment is a list of lists.
environment.append([x for x in line])
# Return the environment (i.e. a list of lists/lines)
return environment
def print_environment(environment, car_position = [0,0]):
"""
This method reads in the environment and current
(y,x) position of the car and prints the environment to the console
:param list environment
:param list car_position
"""
# Store value of current grid square
temp = environment[car_position[0]][car_position[1]]
# Move the car to current grid square
environment[car_position[0]][car_position[1]] = "X"
# Delay
time.sleep(FRAME_TIME)
# Clear the printed output
clear()
# For each line in the environment
for line in environment:
# Initialize a string
text = ""
# Add each character to create a line
for character in line:
text += character
# Print the line of the environment
print(text)
# Retstore value of current grid square
environment[car_position[0]][car_position[1]] = temp
def clear():
"""
This method clears the print output
"""
os.system( 'cls' )
def get_random_start_position(environment):
"""
This method reads in the environment and selects a random
starting position on the racetrack (y, x). Note that
(0,0) corresponds to the upper left corner of the racetrack.
:param list environment: list of lines
:return random starting coordinate (y,x) on the racetrack
:rtype tuple
"""
# Collect all possible starting positions on the racetrack
starting_positions = []
# For each row in the environment
for y,row in enumerate(environment):
# For each column in each row of the environment
for x,col in enumerate(row):
# If we are at the starting position
if col == START:
# Add the coordiante to the list of available
# starting positions in the environment
starting_positions += [(y,x)]
# Random shuffle the list of starting positions
shuffle(starting_positions)
# Select a starting position
return starting_positions[0]
def get_new_velocity(old_vel,accel,min_vel=MIN_VELOCITY,max_vel=MAX_VELOCITY):
"""
Get the new velocity values
:param tuple old_vel: (vy, vx)
:param tuple accel: (ay, ax)
:param int min_vel: Minimum velocity of the car
:param int max_vel: Maximum velocity of the car
:return new velocities in y and x directions
"""
new_y = old_vel[0] + accel[0]
new_x = old_vel[1] + accel[1]
if new_x < min_vel: new_x = min_vel
if new_x > max_vel: new_x = max_vel
if new_y < min_vel: new_y = min_vel
if new_y > max_vel: new_y = max_vel
# Return the new velocities
return new_y, new_x
def get_new_position(old_loc, vel, environment):
"""
Get a new position using the old position and the velocity
:param tuple old_loc: (y,x) position of the car
:param tuple vel: (vy,vx) velocity of the car
:param list environment
:return y+vy, x+vx: (new_y,new_x)
"""
y,x = old_loc[0], old_loc[1]
vy, vx = vel[0], vel[1]
# new_y = y+vy, new_x = x + vx
return y+vy, x+vx
def get_nearest_open_cell(environment, y_crash, x_crash, vy = 0, vx = (
0), open = [TRACK, START, GOAL]):
"""
Locate the nearest open cell in order to handle crash scenario.
Distance is calculated as the Manhattan distance.
Start from the crash grid square and expand outward from there with
a radius of 1, 2, 3, etc. Forms a diamond search pattern.
For example, a Manhattan distance of 2 would look like the following:
.
...
..#..
...
.
If velocity is provided, search in opposite direction of velocity so that
there is no movement over walls
:param list environment
:param int ycrash: y coordinate where crash happened
:param int xcrash: x coordinate where crash happened
:param int vy: velocity in y direction when crash occurred
:param int vx: velocity in x direction when crash occurred
:param list of strings open: Contains environment types
:return tuple of the nearest open y and x position on the racetrack
"""
# Record number of rows (lines) and columns in the environment
rows = len(environment)
cols = len(environment[0])
# Add expanded coverage for searching for nearest open cell
max_radius = max(rows,cols)
# Generate a search radius for each scenario
for radius in range(max_radius):
# If car is not moving in y direction
if vy == 0:
y_off_range = range(-radius, radius + 1)
# If the velocity in y-direction is negative
elif vy < 0:
# Search in the positive direction
y_off_range = range(0, radius + 1)
else:
# Otherwise search in the negative direction
y_off_range = range(-radius, 1)
# For each value in the search radius range of y
for y_offset in y_off_range:
# Start near to crash site and work outwards from there
y = y_crash + y_offset
x_radius = radius - abs(y_offset)
# If car is not moving in x direction
if vx == 0:
x_range = range(x_crash - x_radius, x_crash + x_radius + 1)
# If the velocity in x-direction is negative
elif vx < 0:
x_range = range(x_crash, x_crash + x_radius + 1)
# If the velocity in y-direction is positive
else:
x_range = range(x_crash - x_radius, x_crash + 1)
# For each value in the search radius range of x
for x in x_range:
# We can't go outside the environment(racetrack) boundary
if y < 0 or y >= rows: continue
if x < 0 or x >= cols: continue
# If we find and open cell, return that (y,x) open cell
if environment[y][x] in open:
return(y,x)
# No open grid squares found on the racetrack
return
def act(old_y, old_x, old_vy, old_vx, accel, environment, deterministic=(
False),bad_crash = False):
"""
This method generates the new state s' (position and velocity) from the old
state s and the action a taken by the race car. It also takes as parameters
the two different crash scenarios (i.e. go to nearest
open position on the race track or go back to start)
:param int old_y: The old y position of the car
:param int old_x: The old x position of the car
:param int old_vy: The old y velocity of the car
:param int old_vx: The old x velocity of the car
:param tuple accel: (ay,ax) - acceleration in y and x directions
:param list environment: The racetrack
:param boolean deterministic: True if we always follow the policy
:param boolean bad_crash: True if we return to start after crash
:return s' where s' = new_y, new_x, new_vy, and new_vx
:rtype int
"""
# This method is deterministic if the same output is returned given
# the same input information
if not deterministic:
# If action fails (car fails to take the prescribed action a)
if random() > PROB_ACCELER_SUCCESS:
#print("Car failed to accelerate!")
accel = (0,0)
# Using the old velocity values and the new acceleration values,
# get the new velocity value
new_vy, new_vx = get_new_velocity((old_vy,old_vx), accel)
# Using the new velocity values, update with the new position
temp_y, temp_x = get_new_position((old_y,old_x), (new_vy, new_vx),(
environment))
# Find the nearest open cell on the racetrack to this new position
new_y, new_x = get_nearest_open_cell(environment, temp_y, temp_x, new_vy,
new_vx)
# If a crash happens (i.e. new position is not equal to the nearest
# open position on the racetrack
if new_y != temp_y or new_x != temp_x:
# If this is a crash in which we would have to return to the
# starting position of the racetrack and we are not yet
# on the finish line
if bad_crash and environment[new_y][new_x] != GOAL:
# Return to the start of the race track
new_y, new_x = get_random_start_position(environment)
# Velocity of the race car is set to 0.
new_vy, new_vx = 0,0
# Return the new state
return new_y, new_x, new_vy, new_vx
def get_policy_from_Q(cols, rows, vel_range, Q, actions):
"""
This method returns the policy pi(s) based on the action taken in each state
that maximizes the value of Q in the table Q[s,a]. This is pi*(s)...the
best action that the race car should take in each state is the one that
maximizes the value of Q. (* means optimal)
:param int cols: Number of columns in the environment
:param int rows: Number of rows (i.e. lines) in the environment
:param list vel_range: Range of the velocity of the race car
:param list of tuples actions: actions = [(ay,ax),(ay,ax)....]
:return pi : the policy
:rtype: dictionary: key is the state tuple, value is the
action tuple (ay,ax)
"""
# Create an empty dictionary called pi
pi = {}
# For each state s in the environment
for y in range(rows):
for x in range(cols):
for vy in vel_range:
for vx in vel_range:
# Store the best action for each state...the one that
# maximizes the value of Q.
# argmax looks across all actions given a state and
# returns the index ai of the maximum Q value
pi[(y,x,vy,vx)] = actions[np.argmax(Q[y][x][vy][vx])]
# Return pi(s)
return(pi)
def value_iteration(environment, bad_crash = False, reward = (
0.0), no_training_iter = NO_TRAINING_ITERATIONS):
"""
This method is the value iteration algorithm.
:param list environment
:param boolean bad_crash
:param int reward of the terminal states (i.e. finish line)
:param int no_training_iter
:return policy pi(s) which maps a given state to an optimal action
:rtype dictionary
"""
# Calculate the number of rows and columns of the environment
rows = len(environment)
cols = len(environment[0])
# Create a table V(s) that will store the optimal Q-value for each state.
# This table will help us determine when we should stop the algorithm and
# return the output. Initialize all the values of V(s) to arbitrary values,
# except the terminal state (i.e. finish line state) that has a value of 0.
# values[y][x][vy][vx]
# Read from left to right, we create a list of vx values. Then for each
# vy value we assign the list of vx values. Then for each x value, we assign
# the list of vy values (which contain a list of vx values), etc.
# This is called list comprehension.
values = [[[[random() for _ in vel_range] for _ in vel_range] for _ in (
line)] for line in environment]
# Set the finish line states to 0
for y in range(rows):
for x in range(cols):
# Terminal state has a value of 0
if environment[y][x] == GOAL:
for vy in vel_range:
for vx in vel_range:
values[y][x][vy][vx] = reward
# Initialize all Q(s,a) to arbitrary values, except the terminal state
# (i.e. finish line states) that has a value of 0.
# Q[y][x][vy][vx][ai]
Q = [[[[[random() for _ in actions] for _ in vel_range] for _ in (
vel_range)] for _ in line] for line in environment]
# Set finish line state-action pairs to 0
for y in range(rows):
for x in range(cols):
# Terminal state has a value of 0
if environment[y][x] == GOAL:
for vy in vel_range:
for vx in vel_range:
for ai, a in enumerate(actions):
Q[y][x][vy][vx][ai] = reward
# This is where we train the agent (i.e. race car). Training entails
# optimizing the values in the tables of V(s) and Q(s,a)
for t in range(no_training_iter):
# Keep track of the old V(s) values so we know if we reach stopping
# criterion
values_prev = deepcopy(values)
# When this value gets below the error threshold, we stop training.
# This is the maximum change of V(s)
delta = 0.0
# For all the possible states s in S
for y in range(rows):
for x in range(cols):
for vy in vel_range:
for vx in vel_range:
# If the car crashes into a wall
if environment[y][x] == WALL:
# Wall states have a negative value
# I set some arbitrary negative value since
# we want to train the car not to hit walls
values[y][x][vy][vx] = -9.9
# Go back to the beginning
# of this inner for loop so that we set
# all the other wall states to a negative value
continue
# For each action a in the set of possible actions A
for ai, a in enumerate(actions):
# The reward is -1 for every state except
# for the finish line states
if environment[y][x] == GOAL:
r = reward
else:
r = -1
# Get the new state s'. s' is based on the current
# state s and the current action a
new_y, new_x, new_vy, new_vx = act(
y,x,vy,vx,a,environment,deterministic = True,
bad_crash = bad_crash)
# V(s'): value of the new state when taking action
# a from state s. This is the one step look ahead.
value_of_new_state = values_prev[new_y][new_x][
new_vy][new_vx]
# Get the new state s'. s' is based on the current
# state s and the action (0,0)
new_y, new_x, new_vy, new_vx = act(
y,x,vy,vx,(0,0),environment,deterministic = (
True), bad_crash = bad_crash)
# V(s'): value of the new state when taking action
# (0,0) from state s. This is the value if for some
# reason the race car attemps to accelerate but
# fails
value_of_new_state_if_action_fails = values_prev[
new_y][new_x][new_vy][new_vx]
# Expected value of the new state s'
# Note that each state-action pair has a unique
# value for s'
expected_value = (
PROB_ACCELER_SUCCESS * value_of_new_state) + (
PROB_ACCELER_FAILURE * (
value_of_new_state_if_action_fails))
# Update the Q-value in Q[s,a]
# immediate reward + discounted future value
Q[y][x][vy][vx][ai] = r + (
DISC_RATE * expected_value)
# Get the action with the highest Q value
argMaxQ = np.argmax(Q[y][x][vy][vx])
# Update V(s)
values[y][x][vy][vx] = Q[y][x][vy][vx][argMaxQ]
# Make sure all the rewards to 0 in the terminal state
for y in range(rows):
for x in range(cols):
# Terminal state has a value of 0
if environment[y][x] == GOAL:
for vy in vel_range:
for vx in vel_range:
values[y][x][vy][vx] = reward
# See if the V(s) values are stabilizing
# Finds the maximum change of any of the states. Delta is a float.
delta = max([max([max([max([abs(values[y][x][vy][vx] - values_prev[y][
x][vy][vx]) for vx in vel_range]) for vy in (
vel_range)]) for x in range(cols)]) for y in range(rows)])
# If the values of each state are stabilizing, return the policy
# and exit this method.
if delta < ERROR_THRES:
return(get_policy_from_Q(cols, rows, vel_range, Q, actions))
return(get_policy_from_Q(cols, rows, vel_range, Q, actions))
def do_time_trial(environment, policy, bad_crash = False, animate = True,
max_steps = MAX_STEPS):
"""
Race car will do a time trial on the race track according to the policy.
:param list environment
:param dictionary policy: A dictionary containing the best action for a
given state. The key is the state y,x,vy,vx and value is the action
(ax,ay) acceleration
:param boolean bad_crash: The crash scenario. If true, race car returns to
starting position after crashes
:param boolean animate: If true, show the car on the racetrack at each
timestep
:return i: Total steps to complete race (i.e. from starting position to
finish line)
:rtype int
"""
# Copy the environment
environment_display = deepcopy(environment)
# Get a starting position on the race track
starting_pos = get_random_start_position(environment)
y,x = starting_pos
vy,vx = 0,0 # We initialize velocity to 0
# Keep track if we get stuck
stop_clock = 0
# Begin time trial
for i in range(max_steps):
# Show the race car on the racetrack
if animate:
print_environment(environment_display, car_position = [y,x])
# Get the best action given the current state
a = policy[(y,x,vy,vx)]
# If we are at the finish line, stop the time trial
if environment[y][x] == GOAL:
return i
# Take action and get new a new state s'
y,x,vy,vx = act(y, x, vy, vx, a, environment, bad_crash = bad_crash)
# Determine if the car gets stuck
if vy == 0 and vx == 0:
stop_clock += 1
else:
stop_clock = 0
# We have gotten stuck as the car has not been moving for 5 timesteps
if stop_clock == 5:
return max_steps
# Program has timed out
return max_steps
def main():
"""
The main method of the program
"""
print("Welcome to the Racetrack Control Program!")
print("Powered by the " + ALGORITHM_NAME +
" Reinforcement Learning Algorithm\n")
print("Track: " + THIS_TRACK)
print()
print("What happens to the car if it crashes into a wall?")
option_1 = """1. Starts from the nearest position on the track to the
place where it crashed."""
option_2 = """2. Returns back to the original starting position."""
print(option_1)
print(option_2)
crash_scenario = int(input("Crash scenario (1 or 2): "))
no_training_iter = int(input(
"Enter the initial number of training iterations (e.g. 5): "))
print("\nThe race car is training. Please wait...")
# Directory where the racetrack is located
#racetrack_name = input("Enter the path to your input file: ")
racetrack_name = FILENAME
racetrack = read_environment(racetrack_name)
# How many times the race car will do a single time trial
races = NO_RACES
while(no_training_iter < MAX_TRAIN_ITER):
# Keep track of the total number of steps
total_steps = 0
# Record the crash scenario
bad_crash = False
if crash_scenario == 1:
bad_crash = False
else:
bad_crash = True
# Retrieve the policy
policy = value_iteration(racetrack, bad_crash = bad_crash,
no_training_iter=no_training_iter)
for each_race in range(races):
total_steps += do_time_trial(racetrack, policy, bad_crash = (
bad_crash), animate = True)
print("Number of Training Iterations: " + str(no_training_iter))
if crash_scenario == 1:
print("Bad Crash Scenario: " + option_1)
else:
print("Bad Crash Scenario: " + option_2)
print("Average Number of Steps the Race Car Needs to Take Before " +
"Finding the Finish Line: " + str(total_steps/races) + " steps\n")
print("\nThe race car is training. Please wait...")
# Delay
time.sleep(FRAME_TIME + 4)
# Testing statistics
test_stats_file = THIS_TRACK
test_stats_file += "_"
test_stats_file += ALGORITHM_NAME + "_iter"
test_stats_file += str(no_training_iter)+ "_cr"
test_stats_file += str(crash_scenario) + "_stats.txt"
## Open a test_stats_file
outfile_ts = open(test_stats_file,"w")
outfile_ts.write(
"------------------------------------------------------------------\n")
outfile_ts.write(ALGORITHM_NAME + " Summary Statistics\n")
outfile_ts.write(
"------------------------------------------------------------------\n")
outfile_ts.write("Track: ")
outfile_ts.write(THIS_TRACK)
outfile_ts.write("\nNumber of Training Iterations: " + str(no_training_iter))
if crash_scenario == 1:
outfile_ts.write("\nBad Crash Scenario: " + option_1 + "\n")
else:
outfile_ts.write("Bad Crash Scenario: " + option_2 + "\n")
outfile_ts.write("Average Number of Steps the Race Car Took " +
"Before Finding the Finish Line: " + str(total_steps/races) +
" steps\n")
# Show functioning of the program
trace_runs_file = THIS_TRACK
trace_runs_file += "_"
trace_runs_file += ALGORITHM_NAME + "_iter"
trace_runs_file += str(no_training_iter) + "_cr"
trace_runs_file += str(crash_scenario) + "_trace.txt"
if no_training_iter <= 5:
## Open a new file to save trace runs
outfile_tr = open(trace_runs_file,"w")
# Print trace runs that demonstrate proper functioning of the code
outfile_tr.write(str(policy))
outfile_tr.close()
## Close the files
outfile_ts.close()
no_training_iter += 5
main()
Q-Learning Code in Python
And here is the code for Q-Learning. Again, don’t be scared by how long this code is. I included a lot of comments so that you know what is going on at each step of the code (just copy and paste this into your favorite IDE!):
import os # Library enables the use of operating system dependent functionality
import time # Library handles time-related tasks
from random import shuffle # Import shuffle() method from the random module
from random import random # Import random() method from the random module
from copy import deepcopy # Enable deep copying
import numpy as np # Import Numpy library
# File name: q_learning.py
# Author: Addison Sears-Collins
# Date created: 8/14/2019
# Python version: 3.7
# Description: Implementation of the Q-learning reinforcement learning
# algorithm for the racetrack problem
# The racetrack problem is described in full detail in:
# Barto, A. G., Bradtke, S. J., Singh, S. P. (1995). Learning to Act Using
# Real-time Dynamic Programming. Artificial Intelligence, 72(1-2):81–138.
# and
# Sutton, Richard S., and Andrew G. Barto. Reinforcement learning :
# An Introduction. Cambridge, Massachusetts: The MIT Press, 2018. Print.
# (modified version of Exercise 5.12 on pg. 111)
# Define constants
ALGORITHM_NAME = "Q_Learning"
FILENAME = "L-track.txt"
THIS_TRACK = "L_track"
START = 'S'
GOAL = 'F'
WALL = '#'
TRACK = '.'
MAX_VELOCITY = 5
MIN_VELOCITY = -5
DISC_RATE = 0.9 # Discount rate, also known as gamma. Determines by how much
# we discount the value of a future state s'
ERROR_THRES = 0.001 # Determine when Q-values stabilize (i.e.theta)
PROB_ACCELER_FAILURE = 0.20 # Probability car will try to take action a
# according to policy pi(s) = a and fail.
PROB_ACCELER_SUCCESS = 1 - PROB_ACCELER_FAILURE
NO_TRAINING_ITERATIONS = 500000 # A single training iteration runs through all
# possible states s
TRAIN_ITER_LENGTH = 10 # The maximum length of each training iteration
MAX_TRAIN_ITER = 10000000 # Maximum number of training iterations
NO_RACES = 10 # How many times the race car does a single time trial from
# starting position to the finish line
LEARNING_RATE = 0.25 # If applicable, also known as alpha
MAX_STEPS = 500 # Maximum number of steps the car can take during time trial
FRAME_TIME = 0.1 # How many seconds between frames printed to the console
# Range of the velocity of the race car in both y and x directions
vel_range = range(MIN_VELOCITY, MAX_VELOCITY + 1)
# Actions the race car can take
# (acceleration in y direction, acceleration in x direction)
actions = [(-1,-1), (0,-1), (1,-1),
(-1,0) , (0,0), (1,0),
(-1,1) , (0,1), (1,1)]
def read_environment(filename):
"""
This method reads in the environment (i.e. racetrack)
:param str filename
:return environment: list of lists
:rtype list
"""
# Open the file named filename in READ mode.
# Make the file an object named 'file'
with open(filename, 'r') as file:
# Read until end of file using readline()
# readline() then returns a list of the lines
# of the input file
environment_data = file.readlines()
# Close the file
file.close()
# Initialize an empty list
environment = []
# Adds a counter to each line in the environment_data list,
# i is the index of each line and line is the actual contents.
# enumerate() helps get not only the line of the environment but also
# the index of that line (i.e. row)
for i,line in enumerate(environment_data):
# Ignore the first line that contains the dimensions of the racetrack
if i > 0:
# Remove leading or trailing whitespace if applicable
line = line.strip()
# If the line is empty, ignore it
if line == "": continue
# Creates a list of lines. Within each line is a list of
# individual characters
# The stuff inside append(stuff) first creates a new_list = []
# It then appends all the values in a given line to that new
# list (e.g. new_list.append(all values inside the line))
# Then we append that new list to the environment list.
# Therefoer, environment is a list of lists.
environment.append([x for x in line])
# Return the environment (i.e. a list of lists/lines)
return environment
def print_environment(environment, car_position = [0,0]):
"""
This method reads in the environment and current
(y,x) position of the car and prints the environment to the console
:param list environment
:param list car_position
"""
# Store value of current grid square
temp = environment[car_position[0]][car_position[1]]
# Move the car to current grid square
environment[car_position[0]][car_position[1]] = "X"
# Delay
time.sleep(FRAME_TIME)
# Clear the printed output
clear()
# For each line in the environment
for line in environment:
# Initialize a string
text = ""
# Add each character to create a line
for character in line:
text += character
# Print the line of the environment
print(text)
# Retstore value of current grid square
environment[car_position[0]][car_position[1]] = temp
def clear():
"""
This method clears the print output
"""
os.system( 'cls' )
def get_random_start_position(environment):
"""
This method reads in the environment and selects a random
starting position on the racetrack (y, x). Note that
(0,0) corresponds to the upper left corner of the racetrack.
:param list environment: list of lines
:return random starting coordinate (y,x) on the racetrack
:rtype tuple
"""
# Collect all possible starting positions on the racetrack
starting_positions = []
# For each row in the environment
for y,row in enumerate(environment):
# For each column in each row of the environment
for x,col in enumerate(row):
# If we are at the starting position
if col == START:
# Add the coordiante to the list of available
# starting positions in the environment
starting_positions += [(y,x)]
# Random shuffle the list of starting positions
shuffle(starting_positions)
# Select a starting position
return starting_positions[0]
def act(old_y, old_x, old_vy, old_vx, accel, environment, deterministic=(
False),bad_crash = False):
"""
This method generates the new state s' (position and velocity) from the old
state s and the action a taken by the race car. It also takes as parameters
the two different crash scenarios (i.e. go to nearest
open position on the race track or go back to start)
:param int old_y: The old y position of the car
:param int old_x: The old x position of the car
:param int old_vy: The old y velocity of the car
:param int old_vx: The old x velocity of the car
:param tuple accel: (ay,ax) - acceleration in y and x directions
:param list environment: The racetrack
:param boolean deterministic: True if we always follow the policy
:param boolean bad_crash: True if we return to start after crash
:return s' where s' = new_y, new_x, new_vy, and new_vx
:rtype int
"""
# This method is deterministic if the same output is returned given
# the same input information
if not deterministic:
# If action fails (car fails to take the prescribed action a)
if random() > PROB_ACCELER_SUCCESS:
#print("Car failed to accelerate!")
accel = (0,0)
# Using the old velocity values and the new acceleration values,
# get the new velocity value
new_vy, new_vx = get_new_velocity((old_vy,old_vx), accel)
# Using the new velocity values, update with the new position
temp_y, temp_x = get_new_position((old_y,old_x), (new_vy, new_vx),(
environment))
# Find the nearest open cell on the racetrack to this new position
new_y, new_x = get_nearest_open_cell(environment, temp_y, temp_x, new_vy,
new_vx)
# If a crash happens (i.e. new position is not equal to the nearest
# open position on the racetrack
if new_y != temp_y or new_x != temp_x:
# If this is a crash in which we would have to return to the
# starting position of the racetrack and we are not yet
# on the finish line
if bad_crash and environment[new_y][new_x] != GOAL:
# Return to the start of the race track
new_y, new_x = get_random_start_position(environment)
# Velocity of the race car is set to 0.
new_vy, new_vx = 0,0
# Return the new state
return new_y, new_x, new_vy, new_vx
def get_new_position(old_loc, vel, environment):
"""
Get a new position using the old position and the velocity
:param tuple old_loc: (y,x) position of the car
:param tuple vel: (vy,vx) velocity of the car
:param list environment
:return y+vy, x+vx: (new_y,new_x)
"""
y,x = old_loc[0], old_loc[1]
vy, vx = vel[0], vel[1]
# new_y = y+vy, new_x = x + vx
return y+vy, x+vx
def get_new_velocity(old_vel,accel,min_vel=MIN_VELOCITY,max_vel=MAX_VELOCITY):
"""
Get the new velocity values
:param tuple old_vel: (vy, vx)
:param tuple accel: (ay, ax)
:param int min_vel: Minimum velocity of the car
:param int max_vel: Maximum velocity of the car
:return new velocities in y and x directions
"""
new_y = old_vel[0] + accel[0]
new_x = old_vel[1] + accel[1]
if new_x < min_vel: new_x = min_vel
if new_x > max_vel: new_x = max_vel
if new_y < min_vel: new_y = min_vel
if new_y > max_vel: new_y = max_vel
# Return the new velocities
return new_y, new_x
def get_nearest_open_cell(environment, y_crash, x_crash, vy = 0, vx = (
0), open = [TRACK, START, GOAL]):
"""
Locate the nearest open cell in order to handle crash scenario.
Distance is calculated as the Manhattan distance.
Start from the crash grid square and expand outward from there with
a radius of 1, 2, 3, etc. Forms a diamond search pattern.
For example, a Manhattan distance of 2 would look like the following:
.
...
..#..
...
.
If velocity is provided, search in opposite direction of velocity so that
there is no movement over walls
:param list environment
:param int ycrash: y coordinate where crash happened
:param int xcrash: x coordinate where crash happened
:param int vy: velocity in y direction when crash occurred
:param int vx: velocity in x direction when crash occurred
:param list of strings open: Contains environment types
:return tuple of the nearest open y and x position on the racetrack
"""
# Record number of rows (lines) and columns in the environment
rows = len(environment)
cols = len(environment[0])
# Add expanded coverage for searching for nearest open cell
max_radius = max(rows,cols)
# Generate a search radius for each scenario
for radius in range(max_radius):
# If car is not moving in y direction
if vy == 0:
y_off_range = range(-radius, radius + 1)
# If the velocity in y-direction is negative
elif vy < 0:
# Search in the positive direction
y_off_range = range(0, radius + 1)
else:
# Otherwise search in the negative direction
y_off_range = range(-radius, 1)
# For each value in the search radius range of y
for y_offset in y_off_range:
# Start near to crash site and work outwards from there
y = y_crash + y_offset
x_radius = radius - abs(y_offset)
# If car is not moving in x direction
if vx == 0:
x_range = range(x_crash - x_radius, x_crash + x_radius + 1)
# If the velocity in x-direction is negative
elif vx < 0:
x_range = range(x_crash, x_crash + x_radius + 1)
# If the velocity in y-direction is positive
else:
x_range = range(x_crash - x_radius, x_crash + 1)
# For each value in the search radius range of x
for x in x_range:
# We can't go outside the environment(racetrack) boundary
if y < 0 or y >= rows: continue
if x < 0 or x >= cols: continue
# If we find and open cell, return that (y,x) open cell
if environment[y][x] in open:
return(y,x)
# No open grid squares found on the racetrack
return
def get_policy_from_Q(cols, rows, vel_range, Q, actions):
"""
This method returns the policy pi(s) based on the action taken in each state
that maximizes the value of Q in the table Q[s,a]. This is pi*(s)...the
best action that the race car should take in each state is the one that
maximizes the value of Q. (* means optimal)
:param int cols: Number of columns in the environment
:param int rows: Number of rows (i.e. lines) in the environment
:param list vel_range: Range of the velocity of the race car
:param list of tuples actions: actions = [(ay,ax),(ay,ax)....]
:return pi : the policy
:rtype: dictionary: key is the state tuple, value is the
action tuple (ay,ax)
"""
# Create an empty dictionary called pi
pi = {}
# For each state s in the environment
for y in range(rows):
for x in range(cols):
for vy in vel_range:
for vx in vel_range:
# Store the best action for each state...the one that
# maximizes the value of Q.
# argmax looks across all actions given a state and
# returns the index ai of the maximum Q value
pi[(y,x,vy,vx)] = actions[np.argmax(Q[y][x][vy][vx])]
# Return pi(s)
return(pi)
def q_learning(environment, bad_crash = False, reward = 0.0, no_training_iter =(
NO_TRAINING_ITERATIONS), train_iter_length = TRAIN_ITER_LENGTH):
"""
Return a policy pi that maps states to actions
Each episode uses a different initial state. This forces the agent to fully
explore the environment to create a more informed Q[s,a] table.
:param list environment
:param boolean bad_crash
:param int reward of the terminal states (i.e. finish line)
:param int no_training_iter
:param int train_iter_length
:return policy pi(s) which maps a given state to an optimal action
:rtype dictionary
"""
rows = len(environment)
cols = len(environment[0])
# Initialize all Q(s,a) to arbitrary values, except the terminal state
# (i.e. finish line states) that has a value of 0.
# Q[y][x][vy][vx][ai]
Q = [[[[[random() for _ in actions] for _ in vel_range] for _ in (
vel_range)] for _ in line] for line in environment]
# Set finish line state-action pairs to 0
for y in range(rows):
for x in range(cols):
# Terminal state has a value of 0
if environment[y][x] == GOAL:
for vy in vel_range:
for vx in vel_range:
for ai, a in enumerate(actions):
Q[y][x][vy][vx][ai] = reward
# We run many training iterations for different initial states in order
# to explore the environment as much as possible
for iter in range(no_training_iter):
# Reset all the terminal states to the value of the goal
for y in range(rows):
for x in range(cols):
if environment[y][x] == GOAL:
Q[y][x] = [[[reward for _ in actions] for _ in (
vel_range)] for _ in vel_range]
# Select a random initial state
# from anywhere on the racetrack
y = np.random.choice(range(rows))
x = np.random.choice(range(cols))
vy = np.random.choice(vel_range)
vx = np.random.choice(vel_range)
# Do a certain number of iterations for each episode
for t in range(train_iter_length):
if environment[y][x] == GOAL:
break
if environment[y][x] == WALL:
break
# Choose the best action for the state s
a = np.argmax(Q[y][x][vy][vx])
# Act and then observe a new state s'
new_y, new_x, new_vy, new_vx = act(y, x, vy, vx, actions[
a], environment, bad_crash = bad_crash)
r = -1
# Update the Q table based on the immediate reward received from
# taking action a in state s plus the discounted future reward
Q[y][x][vy][vx][a] = ((1 - LEARNING_RATE)*Q[y][x][vy][vx][a] +
LEARNING_RATE*(r + DISC_RATE*max(Q[new_y][new_x][
new_vy][new_vx])))
# The new state s' now becomes s
y, x, vy, vx = new_y, new_x, new_vy, new_vx
return(get_policy_from_Q(cols, rows, vel_range, Q, actions))
def do_time_trial(environment, policy, bad_crash = False, animate = True,
max_steps = MAX_STEPS):
"""
Race car will do a time trial on the race track according to the policy.
:param list environment
:param dictionary policy: A dictionary containing the best action for a
given state. The key is the state y,x,vy,vx and value is the action
(ax,ay) acceleration
:param boolean bad_crash: The crash scenario. If true, race car returns to
starting position after crashes
:param boolean animate: If true, show the car on the racetrack at each
timestep
:return i: Total steps to complete race (i.e. from starting position to
finish line)
:rtype int
"""
# Copy the environment
environment_display = deepcopy(environment)
# Get a starting position on the race track
starting_pos = get_random_start_position(environment)
y,x = starting_pos
vy,vx = 0,0 # We initialize velocity to 0
# Keep track if we get stuck
stop_clock = 0
# Begin time trial
for i in range(max_steps):
# Show the race car on the racetrack
if animate:
print_environment(environment_display, car_position = [y,x])
# Get the best action given the current state
a = policy[(y,x,vy,vx)]
# If we are at the finish line, stop the time trial
if environment[y][x] == GOAL:
return i
# Take action and get new a new state s'
y,x,vy,vx = act(y, x, vy, vx, a, environment, bad_crash = bad_crash)
# Determine if the car gets stuck
if vy == 0 and vx == 0:
stop_clock += 1
else:
stop_clock = 0
# We have gotten stuck as the car has not been moving for 5 timesteps
if stop_clock == 5:
return max_steps
# Program has timed out
return max_steps
def main():
"""
The main method of the program
"""
print("Welcome to the Racetrack Control Program!")
print("Powered by the " + ALGORITHM_NAME +
" Reinforcement Learning Algorithm\n")
print("Track: " + THIS_TRACK)
print()
print("What happens to the car if it crashes into a wall?")
option_1 = """1. Starts from the nearest position on the track to the
place where it crashed."""
option_2 = """2. Returns back to the original starting position."""
print(option_1)
print(option_2)
crash_scenario = int(input("Crash scenario (1 or 2): "))
no_training_iter = int(input(
"Enter the initial number of training iterations (e.g. 500000): "))
print("\nThe race car is training. Please wait...")
# Directory where the racetrack is located
#racetrack_name = input("Enter the path to your input file: ")
racetrack_name = FILENAME
racetrack = read_environment(racetrack_name)
# How many times the race car will do a single time trial
races = NO_RACES
while(no_training_iter <= MAX_TRAIN_ITER):
# Keep track of the total number of steps
total_steps = 0
# Record the crash scenario
bad_crash = False
if crash_scenario == 1:
bad_crash = False
else:
bad_crash = True
# Retrieve the policy
policy = q_learning(racetrack, bad_crash = (
bad_crash),no_training_iter=no_training_iter)
for each_race in range(races):
total_steps += do_time_trial(racetrack, policy, bad_crash = (
bad_crash), animate = False)
print("Number of Training Iterations: " + str(no_training_iter))
if crash_scenario == 1:
print("Bad Crash Scenario: " + option_1)
else:
print("Bad Crash Scenario: " + option_2)
print("Average Number of Steps the Race Car Needs to Take Before " +
"Finding the Finish Line: " + str(total_steps/races) + " steps\n")
print("\nThe race car is training. Please wait...")
# Delay
time.sleep(FRAME_TIME + 4)
# Testing statistics
test_stats_file = THIS_TRACK
test_stats_file += "_"
test_stats_file += ALGORITHM_NAME + "_iter"
test_stats_file += str(no_training_iter)+ "_cr"
test_stats_file += str(crash_scenario) + "_stats.txt"
## Open a test_stats_file
outfile_ts = open(test_stats_file,"w")
outfile_ts.write(
"------------------------------------------------------------------\n")
outfile_ts.write(ALGORITHM_NAME + " Summary Statistics\n")
outfile_ts.write(
"------------------------------------------------------------------\n")
outfile_ts.write("Track: ")
outfile_ts.write(THIS_TRACK)
outfile_ts.write("\nNumber of Training Iterations: " + str(no_training_iter))
if crash_scenario == 1:
outfile_ts.write("\nBad Crash Scenario: " + option_1 + "\n")
else:
outfile_ts.write("Bad Crash Scenario: " + option_2 + "\n")
outfile_ts.write("Average Number of Steps the Race Car Took " +
"Before Finding the Finish Line: " + str(total_steps/races) +
" steps\n")
# Show functioning of the program
trace_runs_file = THIS_TRACK
trace_runs_file += "_"
trace_runs_file += ALGORITHM_NAME + "_iter"
trace_runs_file += str(no_training_iter) + "_cr"
trace_runs_file += str(crash_scenario) + "_trace.txt"
if no_training_iter <= 5:
## Open a new file to save trace runs
outfile_tr = open(trace_runs_file,"w")
# Print trace runs that demonstrate proper functioning of the code
outfile_tr.write(str(policy))
outfile_tr.close()
## Close the files
outfile_ts.close()
if no_training_iter == 500000:
no_training_iter += 500000
else:
no_training_iter += 1000000
main()
Experimental Output and Analysis
Here are the results:
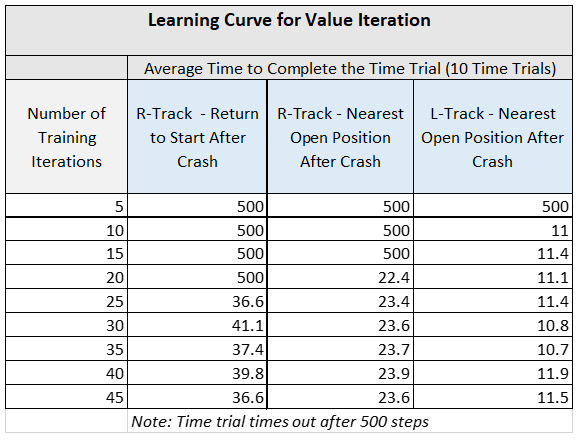
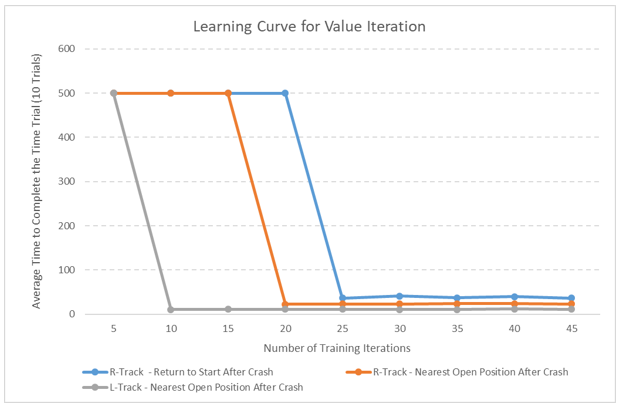
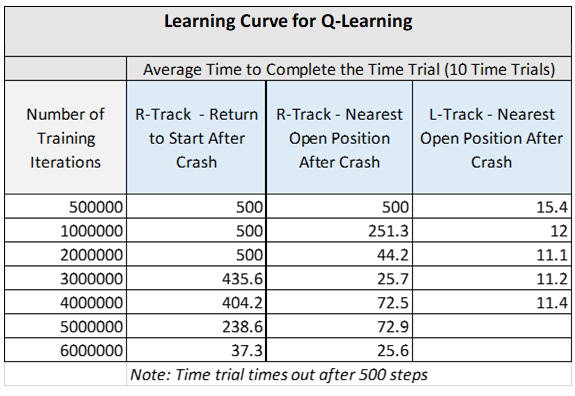
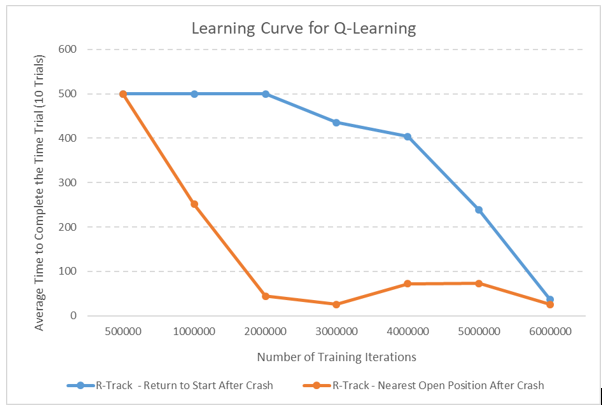
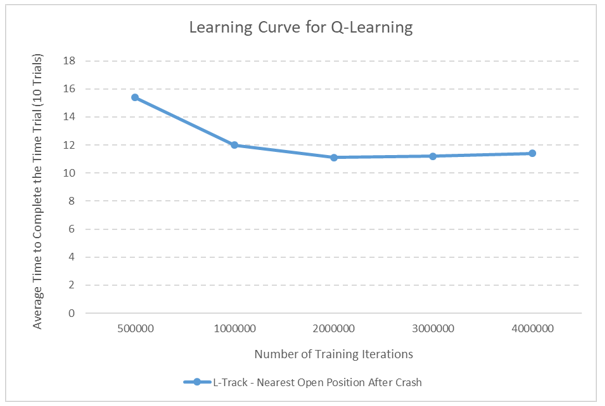
Analysis
Hypothesis 1: Both Algorithms Will Enable the Car to Finish the Race
Both the value iteration and Q-learning algorithms were successfully able to finish the race for both crash scenarios and for both the R-track and the L-track. The race car completed the R-track in fewer time steps than the L-track, which was expected.
The crash policy in which the car had to return to the starting position after it crashed versus going to the nearest open position negatively impacted performance for both algorithms. Time trial performance was superior for the value iteration algorithm compared to the Q learning algorithm. This result was expected given that the value iteration algorithm had access to the transition and the reward probabilities during the training phase. In other words, value iteration it gets a complete model of the entire track, whereas Q-learning has to be forced to explore the environment in order to learn.
Hypothesis 2: Value Iteration Will Learn Faster Than Q-Learning
My hypothesis was correct. Value iteration generated a learning policy faster than Q-learning because it had access to the transition and reward functions. Q-learning required more than 6,000,000 training iterations on the R-track to achieve the time trial performance that the value iteration algorithm was able to produce in only 45 training iterations (holding all other hyperparameters constant). And whereas the Q-learning algorithm took 2-3 hours to train to get good time trial results, value iteration never took more than 10 minutes for both the R-track and L-track under both of the bad crash scenarios.
Hypothesis 3: Bad Crash Version 1 Will Outperform Bad Crash Version 2
The results show that my hypothesis was correct. It took longer for the car to finish the race for the crash scenario in which the race car needed to return to the original starting position each time it crashed into a wall. In other words, Bad Crash Version 1 (return to start) performance was better than Bad Crash Version 2 (return to nearest open position) performance. These results are what I expected since always returning to the starting position after a crash hampers the ability of the race car to continually explore new states.
Summary and Conclusions
My hypotheses were correct. Here are the following conclusions:
- Value iteration and Q-learning are powerful reinforcement learning algorithms that can enable an agent to learn autonomously.
- Value iteration led to faster learning than the Q-learning algorithm.
- A crash policy in which the race car always returns to the starting position after a crash negatively impacts performance.
Video Demonstration
Here is a video demonstration of the algorithms in action.
References
Alpaydin, E. (2014). Introduction to Machine Learning. Cambridge, Massachusetts: The MIT Press.
Barto, A. G., Bradtke, S. J., & Singh, S. P. (1995). Learning to Act Using Real-Time Dynamic Programming. Artificial Intelligence, 81-138.
Russell, S. J., Norvig, P., & Davis, E. (2010). Artificial intelligence : A Modern Approach. Upper Saddle River, NJ: Prentice Hall.
Sutton, R. S., & Barto, A. G. (2018). Reinforcement learning : An Introduction . Cambridge, Massachusetts: The MIT Press.