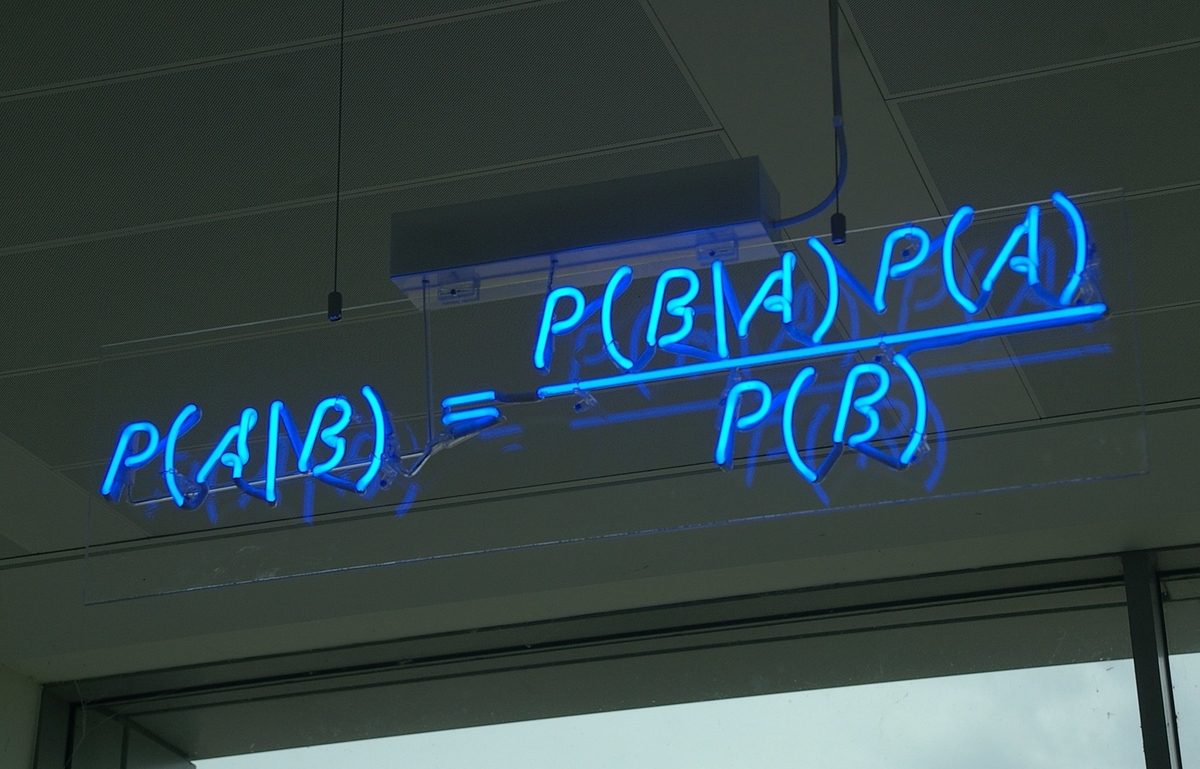In this post, I will walk you through the Naive Bayes machine learning algorithm, step-by-step. We will develop the code for the algorithm from scratch using Python. We’ll then run the algorithm on real-world data sets from the UCI Machine Learning Repository. On one of the data sets, we’ll predict if a patient has breast cancer or not based on ten different attributes. Let’s get started!
Table of Contents
- What is Naive Bayes?
- Algorithm Steps
- Training Phase
- Testing Phase
- Naive Bayes Implementation
- Naive Bayes Algorithm in Python, Coded From Scratch
- Output Statistics of Naive Bayes
What is Naive Bayes?
The Naive Bayes algorithm is a technique based on Bayes Theorem for calculating the probability of a hypothesis (H) given some pieces of evidence (E).
For example, suppose we are trying to identify if a person is sick or not. Our hypothesis is that the person is sick.
We would naturally take a look at the evidence (eye color, body temperature, blood pressure, etc.) to determine if the person is sick or not. Each piece of evidence provides us clues. From that evidence, we can then use the Naive Bayes algorithm to calculate two probabilities:
- Probability 1: The probability that the person is sick given she has red eyes, a body temperature of 99°F, and has normal blood pressure.
- Probability 2: The probability that the person is not sick given she has red eyes, a body temperature of 99°F, and has normal blood pressure.
We then classify the person as being sick or not based on which probability (Probability 1 vs. Probability 2) is the highest.
Mathematically, Bayes theorem can be expressed as follows:
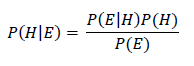
Or in expanded form, we have:
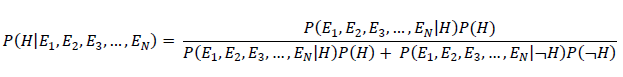
Or…
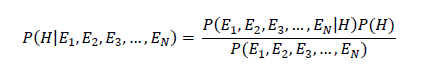
Where:
- P = probability
- | = given
- E = evidence (e.g. red eyes, body temperature, etc.)
- H = hypothesis (e.g. sick)
- ¬ = not
- P(H|E1, E2,E3,…,EN) = posterior probability: the probability of a hypothesis after taking the evidence into account (e.g. probability of being sick given all this evidence)
- P(E1, E2,E3,…,EN|H)= likelihood: the probability of the evidence given the hypothesis (e.g. probability of having red eyes given that a person is sick)
- P(H) = class prior probability: the known probability of the hypothesis (e.g. probability of being sick for the population or entire sample of instances)
The equation above says: “The probability of the hypothesis (e.g. a person is sick) given the evidence (e.g. eye color, body temperature, blood pressure) is equal to the probability of the evidence given the hypothesis times the probability of the hypothesis divided by the probability of the evidence.”
The key assumption with the Bayes theorem is that all of the attributes are conditionally independent. In other words, the occurrence of one piece of evidence gives no information about the probability of another piece of evidence occurring.
For example, Bayes theorem would assume that the probability of having red eyes gives no information about the probability of having a high body temperature. We know this is not often the case. Such an assumption is naive, and that is why we call this classification algorithm the Naive Bayes algorithm.
We can therefore rewrite the equation based on the probability rule of conditional independence, which is:
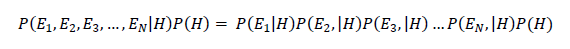
Bayes equation can be rewritten as:
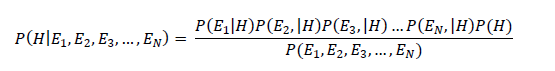
Algorithm Steps
Training Phase
Recall in Naive Bayes, for a 2-class classification problem (e.g. sick or not sick), we need to calculate two probabilities for each instance. The highest probability is our prediction.:
Probability 1 (sick): The probability that the person is sick given she has red eyes, a body temperature of 99°F, and has normal blood pressure.
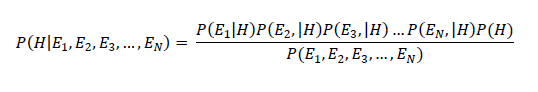
Probability 2 (not sick): The probability that the person is not sick given she has red eyes, a body temperature of 99°F, and has a normal blood pressure.
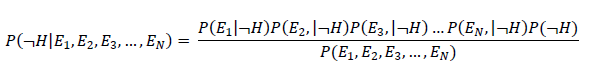
If Probability 1 > Probability 2, she is sick. Otherwise, she is not sick
Notice, the denominators above are both equal. Because they are both equal, we can ignore them for training our model since all we need to do is to compare the numerators.
- Probability 1 (sick): The probability that the person is sick given she has red eyes, a body temperature of 99°F, and has a normal blood pressure.
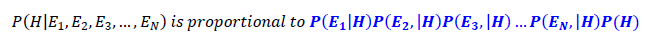
- Probability 2 (not sick): The probability that the person is not sick given she has red eyes, a body temperature of 99°F, and has a normal blood pressure.
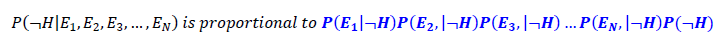
This makes our lives easier, since now all Naive Bayes algorithm needs to do to train on a data set is to calculate those values in blue above in order to make a classification prediction (sick or not sick). That is, we need to calculate two class prior probabilities (sick or not sick for the whole sample or population) plus the conditional probability of each unique value in each attribute for each class:
Number of Probabilities Calculated during Training Phase of Naive Bayes = 2 class prior probabilities + 2 * (# of unique values for E1) + 2 * (# of unique values for E2) + … 2 * (# of unique values for EN)
If all pieces of evidence were binary (e.g. red eyes, no red eyes) and the class is binary (sick or not sick), we would need to calculate four probabilities for each attribute. The total number of probabilities calculated in the training phase is therefore (where N is the number of attributes):
Number of Probabilities Calculated during Training Phase of Naive Bayes = 2 + 4N
For example, let’s see all the probabilities that would need to be calculated for binary attribute E1 (e.g. red eyes or no red eyes):

We have our two class prior probabilities. These will be the same for all attributes:
- P(1) = (Total number of people that are sick in the training data set) / (Total number of people in the training data set)
- P(0) = (Total number of people that are not sick in the training data set) / (Total number of people in the training data set)
And since (N = number, S = total number of instances in the training data set)…
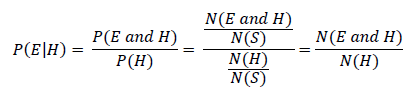
To complete the table for attribute E1, we calculate four different probabilities:

We have to store these probabilities somewhere so they can be looked up during the testing phase. In my program, I stored them in a Python dictionary, with the following search key: <attribute_name><attribute_value><class_value>.
For example, the search key redeyes01, would return the probability of not having red eyes given someone is sick:
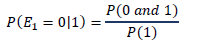
That’s it. Once we have the tables for each attribute along with the class prior probabilities, the algorithm can go to work and make predictions for new instances.
Testing Phase
Having calculated the required probabilities and stored them somewhere, the algorithm is ready to make its predictions for new instances. As mentioned in the previous section, for each instance (i.e. row of the testing data set), two calculations need to be made and then the results are compared.
1. Probability 1 (sick): The probability that the person is sick given she has red eyes, a body temperature of 99°F, and has normal blood pressure.
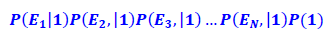
2.Probability 2 (not sick): The probability that the person is not sick given she has red eyes, a body temperature of 99°F, and has a normal blood pressure.
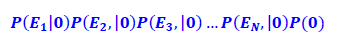
3. If Probability 1 > Probability 2, she is sick. Otherwise, she is not sick
4. Proceed to the next instance and repeat 1-3.
Naive Bayes Implementation
The Naive Bayes algorithm was implemented from scratch. The Breast Cancer, Glass, Iris, Soybean (small), and Vote data sets were preprocessed to meet the input requirements of the algorithms. I used five-fold stratified cross-validation to evaluate the performance of the models.
Required Data Set Format for Naïve Bayes
Columns (0 through N)
- 0: Instance ID
- 1: Attribute 1
- 2: Attribute 2
- 3: Attribute 3
- …
- N: Actual Class
The program then adds two additional columns for the testing set.
- N + 1: Predicted Class
- N + 2: Prediction Correct? (1 if yes, 0 if no)
Breast Cancer Data Set
This breast cancer data set contains 699 instances, 10 attributes, and a class – malignant or benign (Wolberg, 1992).
Modification of Attribute Values
The actual class value was changed to “Benign” or “Malignant.”
I transformed the attributes into binary numbers so that the algorithms could process the data properly and efficiently. If attribute value was greater than 5, the value was changed to 1, otherwise it was 0.
Missing Data
There were 16 missing attribute values, each denoted with a “?”. I chose a random number between 1 and 10 (inclusive) to fill in the data.
Glass Data Set
This glass data set contains 214 instances, 10 attributes, and 7 classes (German, 1987). The purpose of the data set is to identify the type of glass.
Modification of Attribute Values
If attribute values were greater than the median of the attribute, value was changed to 1, otherwise it was set to 0.
Missing Data
There are no missing values in this data set.
Iris Data Set
This data set contains 3 classes of 50 instances each (150 instances in total), where each class refers to a different type of iris plant (Fisher, 1988).
Modification of Attribute Values
If attribute values were greater than the median of the attribute, value was changed to 1, otherwise it was set to 0.
Missing Data
There were no missing attribute values.
Soybean Data Set (small)
This soybean (small) data set contains 47 instances, 35 attributes, and 4 classes (Michalski, 1980). The purpose of the data set is to determine the disease type.
Modification of Attribute Values
If attribute values were greater than the median of the attribute, value was changed to 1, otherwise it was set to 0.
Missing Data
There are no missing values in this data set.
Vote Data Set
This data set includes votes for each of the U.S. House of Representatives Congressmen (435 instances) on the 16 key votes identified by the Congressional Quarterly Almanac (Schlimmer, 1987). The purpose of the data set is to identify the representative as either a Democrat or Republican.
- 267 Democrats
- 168 Republicans
Modification of Attribute Values
I did the following modifications:
- Changed all “y” to 1 and all “n” to 0.
Missing Data
Missing values were denoted as “?”. To fill in those missing values, I chose random number, either 0 (“No”) or 1 (“Yes”).
Naive Bayes Algorithm in Python, Coded From Scratch
Here are the input files for the code below:
Here is the driver code that contains the main method. I recommend copying and pasting it into a text editor like Notepad++ or an IDE so that you don’t have to do any horizontal scrolling to see the entire code. The code is long (don’t be scared!), but that is because it includes a ton of notes so that you know what is going on:
import pandas as pd # Import Pandas library
import numpy as np # Import Numpy library
import five_fold_stratified_cv
import naive_bayes
# File name: naive_bayes_driver.py
# Author: Addison Sears-Collins
# Date created: 7/17/2019
# Python version: 3.7
# Description: Driver for the naive_bayes.py program
# (Naive Bayes)
# Required Data Set Format for Disrete Class Values
# Columns (0 through N)
# 0: Instance ID
# 1: Attribute 1
# 2: Attribute 2
# 3: Attribute 3
# ...
# N: Actual Class
# The naive_bayes.py program then adds 2 additional columns for the test set.
# N + 1: Predicted Class
# N + 2: Prediction Correct? (1 if yes, 0 if no)
ALGORITHM_NAME = "Naive Bayes"
SEPARATOR = "," # Separator for the data set (e.g. "\t" for tab data)
def main():
print("Welcome to the " + ALGORITHM_NAME + " Program!")
print()
# Directory where data set is located
data_path = input("Enter the path to your input file: ")
#data_path = "breast_cancer.txt"
# Read the full text file and store records in a Pandas dataframe
pd_data_set = pd.read_csv(data_path, sep=SEPARATOR)
# Show functioning of the program
trace_runs_file = input("Enter the name of your trace runs file: ")
#trace_runs_file = "breast_cancer_naive_bayes_trace_runs.txt"
# Open a new file to save trace runs
outfile_tr = open(trace_runs_file,"w")
# Testing statistics
test_stats_file = input("Enter the name of your test statistics file: ")
#test_stats_file = "breast_cancer_naive_bayes_test_stats.txt"
# Open a test_stats_file
outfile_ts = open(test_stats_file,"w")
# The number of folds in the cross-validation
NO_OF_FOLDS = 5
# Generate the five stratified folds
fold0, fold1, fold2, fold3, fold4 = five_fold_stratified_cv.get_five_folds(
pd_data_set)
training_dataset = None
test_dataset = None
# Create an empty array of length 5 to store the accuracy_statistics
# (classification accuracy)
accuracy_statistics = np.zeros(NO_OF_FOLDS)
# Run Naive Bayes the designated number of times as indicated by the
# number of folds
for experiment in range(0, NO_OF_FOLDS):
print()
print("Running Experiment " + str(experiment + 1) + " ...")
print()
outfile_tr.write("Running Experiment " + str(experiment + 1) + " ...\n")
outfile_tr.write("\n")
# Each fold will have a chance to be the test data set
if experiment == 0:
test_dataset = fold0
training_dataset = pd.concat([
fold1, fold2, fold3, fold4], ignore_index=True, sort=False)
elif experiment == 1:
test_dataset = fold1
training_dataset = pd.concat([
fold0, fold2, fold3, fold4], ignore_index=True, sort=False)
elif experiment == 2:
test_dataset = fold2
training_dataset = pd.concat([
fold0, fold1, fold3, fold4], ignore_index=True, sort=False)
elif experiment == 3:
test_dataset = fold3
training_dataset = pd.concat([
fold0, fold1, fold2, fold4], ignore_index=True, sort=False)
else:
test_dataset = fold4
training_dataset = pd.concat([
fold0, fold1, fold2, fold3], ignore_index=True, sort=False)
# Run Naive Bayes
accuracy, predictions, learned_model, no_of_instances_test = (
naive_bayes.naive_bayes(training_dataset,test_dataset))
# Replace 1 with Yes and 0 with No in the 'Prediction
# Correct?' column
predictions['Prediction Correct?'] = predictions[
'Prediction Correct?'].map({1: "Yes", 0: "No"})
# Print the trace runs of each experiment
print("Accuracy:")
print(str(accuracy * 100) + "%")
print()
print("Classifications:")
print(predictions)
print()
print("Learned Model (Likelihood Table):")
print(learned_model)
print()
print("Number of Test Instances:")
print(str(no_of_instances_test))
print()
outfile_tr.write("Accuracy:")
outfile_tr.write(str(accuracy * 100) + "%\n\n")
outfile_tr.write("Classifications:\n")
outfile_tr.write(str(predictions) + "\n\n")
outfile_tr.write("Learned Model (Likelihood Table):\n")
outfile_tr.write(str(learned_model) + "\n\n")
outfile_tr.write("Number of Test Instances:")
outfile_tr.write(str(no_of_instances_test) + "\n\n")
# Store the accuracy in the accuracy_statistics array
accuracy_statistics[experiment] = accuracy
outfile_tr.write("Experiments Completed.\n")
print("Experiments Completed.\n")
# Write to a file
outfile_ts.write("----------------------------------------------------------\n")
outfile_ts.write(ALGORITHM_NAME + " Summary Statistics\n")
outfile_ts.write("----------------------------------------------------------\n")
outfile_ts.write("Data Set : " + data_path + "\n")
outfile_ts.write("\n")
outfile_ts.write("Accuracy Statistics for All 5 Experiments:")
outfile_ts.write(np.array2string(
accuracy_statistics, precision=2, separator=',',
suppress_small=True))
outfile_ts.write("\n")
outfile_ts.write("\n")
accuracy = np.mean(accuracy_statistics)
accuracy *= 100
outfile_ts.write("Classification Accuracy : " + str(accuracy) + "%\n")
# Print to the console
print()
print("----------------------------------------------------------")
print(ALGORITHM_NAME + " Summary Statistics")
print("----------------------------------------------------------")
print("Data Set : " + data_path)
print()
print()
print("Accuracy Statistics for All 5 Experiments:")
print(accuracy_statistics)
print()
print()
print("Classification Accuracy : " + str(accuracy) + "%")
print()
# Close the files
outfile_tr.close()
outfile_ts.close()
main()
Here is the code for Naive Bayes:
import pandas as pd # Import Pandas library
import numpy as np # Import Numpy library
# File name: naive_bayes.py
# Author: Addison Sears-Collins
# Date created: 7/17/2019
# Python version: 3.7
# Description: Implementation of Naive Bayes
# This code works for multi-class
# classification problems (e.g. democrat/republican/independent)
# Calculate P(E1|CL0)P(E2|CL0)P(E3|CL0)...P(E#|CL0) * P(CL0) and
# P(E1|CL1)P(E2|CL1)P(E3|CL1)...P(E#|CL1) * P(CL1) and
# P(E1|CL2)P(E2|CL2)P(E3|CL2)...P(E#|CL2) * P(CL2), etc. and
# predict the class with the maximum result.
# E is an attribute, and CL means class.
# Only need class prior probability and likelihoods to make a prediction
# (i.e. the numerator of Bayes formula) since denominators are
# same for both the P(CL0|E1,E2,E3...)*P(CL0) and
# P(CL1|E1,E2,E3...)*P(CL1), etc. cases where P means "probability of"
# and | means "given".
# Required Data Set Format for Disrete Class Values
# Columns (0 through N)
# 0: Instance ID
# 1: Attribute 1
# 2: Attribute 2
# 3: Attribute 3
# ...
# N: Actual Class
# This program then adds 2 additional columns for the test set.
# N + 1: Predicted Class
# N + 2: Prediction Correct? (1 if yes, 0 if no)
def naive_bayes(training_set,test_set):
"""
Parameters:
training_set: The training instances as a Pandas dataframe
test_set: The test instances as a Pandas dataframe
Returns:
accuracy: Classification accuracy as a decimal
predictions: Classifications of all the test instances as a
Pandas dataframe
learned_model: The likelihood table that is produced
during the training phase
no_of_instances_test: The number of test instances
"""
# Calculate the number of instances, columns, and attributes in the
# training data set. Assumes 1 column for the instance ID and 1 column
# for the class. Record the index of the column that contains
# the actual class
no_of_instances_train = len(training_set.index) # number of rows
no_of_columns_train = len(training_set.columns) # number of columns
no_of_attributes = no_of_columns_train - 2
actual_class_column = no_of_columns_train - 1
# Store class values in a column, sort them, then create a list of unique
# classes and store in a dataframe and a Numpy array
unique_class_list_df = training_set.iloc[:,actual_class_column]
unique_class_list_df = unique_class_list_df.sort_values()
unique_class_list_np = unique_class_list_df.unique() #Numpy array
unique_class_list_df = unique_class_list_df.drop_duplicates()#Pandas df
# Record the number of unique classes in the data set
num_unique_classes = len(unique_class_list_df)
# Record the frequency counts of each class in a Numpy array
freq_cnt_class = training_set.iloc[:,actual_class_column].value_counts(
sort=True)
# Record the frequency percentages of each class in a Numpy array
# This is a list of the class prior probabilities
class_prior_probs = training_set.iloc[:,actual_class_column].value_counts(
normalize=True, sort=True)
# Add 2 additional columns to the testing dataframe
test_set = test_set.reindex(
columns=[*test_set.columns.tolist(
), 'Predicted Class', 'Prediction Correct?'])
# Calculate the number of instances and columns in the
# testing data set. Record the index of the column that contains the
# predicted class and prediction correctness (1 if yes; 0 if no)
no_of_instances_test = len(test_set.index) # number of rows
no_of_columns_test = len(test_set.columns) # number of columns
predicted_class_column = no_of_columns_test - 2
prediction_correct_column = no_of_columns_test - 1
######################### Training Phase of the Model #####################
# Create a an empty dictionary
my_dict = {}
# Calculate the likelihood tables for each attribute. If an attribute has
# four levels, there are (# of unique classes x 4) different probabilities
# that need to be calculated for that attribute.
# Start on the first attribute and make your way through all the attributes
for col in range(1, no_of_attributes + 1):
# Record the name of this column
colname = training_set.columns[col]
# Create a dataframe containing the unique values in the column
unique_attribute_values_df = training_set[colname].drop_duplicates()
# Create a Numpy array containing the unique values in the column
unique_attribute_values_np = training_set[colname].unique()
# Calculate likelihood of the attribute given each unique class value
for class_index in range (0, num_unique_classes):
# For each unique attribute value, calculate the likelihoods
# for each class
for attr_val in range (0, unique_attribute_values_np.size) :
running_sum = 0
# Calculate N(unique attribute value and class value)
# Where N means "number of"
# Go through each row of the training set
for row in range(0, no_of_instances_train):
if (training_set.iloc[row,col] == (
unique_attribute_values_df.iloc[attr_val])) and (
training_set.iloc[row, actual_class_column] == (
unique_class_list_df.iloc[class_index])):
running_sum += 1
# With N(unique attribute value and class value) as the numerator
# we now need to divide by the total number of times the class
# appeared in the data set
try:
denominator = freq_cnt_class[class_index]
except:
denominator = 1.0
likelihood = min(1.0,(running_sum / denominator))
# Add a new likelihood to the dictionary
# Format of search key is
# <attribute_name><attribute_value><class_value>
search_key = str(colname) + str(
unique_attribute_values_df.iloc[
attr_val]) + str(unique_class_list_df.iloc[
class_index])
my_dict[search_key] = likelihood
# Print the likelihood table to the console
learned_model = pd.DataFrame.from_dict(my_dict, orient='index')
################# End of Training Phase of the Naive Bayes Model ########
################# Testing Phase of the Naive Bayes Model ################
# Proceed one instance at a time and calculate the prediction
for row in range(0, no_of_instances_test):
# Initialize the prediction outcome
predicted_class = unique_class_list_df.iloc[0]
max_numerator_of_bayes = 0.0
# Calculate the Bayes equation numerator for each test instance
# That is: P(E1|CL0)P(E2|CL0)P(E3|CL0)...P(E#|CL0) * P(CL0),
# P(E1|CL1)P(E2|CL1)P(E3|CL1)...P(E#|CL1) * P(CL1)...
for class_index in range (0, num_unique_classes):
# Reset the running product with the class
# prior probability, P(CL)
try:
running_product = class_prior_probs[class_index]
except:
running_product = 0.0000001 # Class not found in data set
# Calculation of P(CL) * P(E1|CL) * P(E2|CL) * P(E3|CL)...
# Format of search key is
# <attribute_name><attribute_value><class_value>
# Record each search key value
for col in range(1, no_of_attributes + 1):
attribute_name = test_set.columns[col]
attribute_value = test_set.iloc[row,col]
class_value = unique_class_list_df.iloc[class_index]
# Set the search key
key = str(attribute_name) + str(
attribute_value) + str(class_value)
# Update the running product
try:
running_product *= my_dict[key]
except:
running_product *= 0
# Record the prediction if we have a new max
# Bayes numerator
if running_product > max_numerator_of_bayes:
max_numerator_of_bayes = running_product
predicted_class = unique_class_list_df.iloc[
class_index] # New predicted class
# Store the prediction in the dataframe
test_set.iloc[row,predicted_class_column] = predicted_class
# Store if the prediction was correct
if predicted_class == test_set.iloc[row,actual_class_column]:
test_set.iloc[row,prediction_correct_column] = 1
else:
test_set.iloc[row,prediction_correct_column] = 0
# Store the revamped dataframe
predictions = test_set
# accuracy = (total correct predictions)/(total number of predictions)
accuracy = (test_set.iloc[
:,prediction_correct_column].sum())/no_of_instances_test
# Return statement
return accuracy, predictions, learned_model, no_of_instances_test
####################### End Testing Phase #################################
Here is the code for five-fold stratified cross-validation:
import pandas as pd # Import Pandas library
import numpy as np # Import Numpy library
# File name: five_fold_stratified_cv.py
# Author: Addison Sears-Collins
# Date created: 7/17/2019
# Python version: 3.7
# Description: Implementation of five-fold stratified cross-validation
# Divide the data set into five random groups. Make sure
# that the proportion of each class in each group is roughly equal to its
# proportion in the entire data set.
# Required Data Set Format for Disrete Class Values
# Columns (0 through N)
# 0: Instance ID
# 1: Attribute 1
# 2: Attribute 2
# 3: Attribute 3
# ...
# N: Actual Class
def get_five_folds(instances):
"""
Parameters:
instances: A Pandas data frame containing the instances
Returns:
fold0, fold1, fold2, fold3, fold4
Five folds whose class frequency distributions are
each representative of the entire original data set (i.e. Five-Fold
Stratified Cross Validation)
"""
# Shuffle the data set randomly
instances = instances.sample(frac=1).reset_index(drop=True)
# Record the number of columns in the data set
no_of_columns = len(instances.columns) # number of columns
# Record the number of rows in the data set
no_of_rows = len(instances.index) # number of rows
# Create five empty folds (i.e. Panda Dataframes: fold0 through fold4)
fold0 = pd.DataFrame(columns=(instances.columns))
fold1 = pd.DataFrame(columns=(instances.columns))
fold2 = pd.DataFrame(columns=(instances.columns))
fold3 = pd.DataFrame(columns=(instances.columns))
fold4 = pd.DataFrame(columns=(instances.columns))
# Record the column of the Actual Class
actual_class_column = no_of_columns - 1
# Generate an array containing the unique
# Actual Class values
unique_class_list_df = instances.iloc[:,actual_class_column]
unique_class_list_df = unique_class_list_df.sort_values()
unique_class_list_np = unique_class_list_df.unique() #Numpy array
unique_class_list_df = unique_class_list_df.drop_duplicates()#Pandas df
unique_class_list_np_size = unique_class_list_np.size
# For each unique class in the unique Actual Class array
for unique_class_list_np_idx in range(0, unique_class_list_np_size):
# Initialize the counter to 0
counter = 0
# Go through each row of the data set and find instances that
# are part of this unique class. Distribute them among one
# of five folds
for row in range(0, no_of_rows):
# If the value of the unique class is equal to the actual
# class in the original data set on this row
if unique_class_list_np[unique_class_list_np_idx] == (
instances.iloc[row,actual_class_column]):
# Allocate instance to fold0
if counter == 0:
# Extract data for the new row
new_row = instances.iloc[row,:]
# Append that entire instance to fold
fold0.loc[len(fold0)] = new_row
# Increase the counter by 1
counter += 1
# Allocate instance to fold1
elif counter == 1:
# Extract data for the new row
new_row = instances.iloc[row,:]
# Append that entire instance to fold
fold1.loc[len(fold1)] = new_row
# Increase the counter by 1
counter += 1
# Allocate instance to fold2
elif counter == 2:
# Extract data for the new row
new_row = instances.iloc[row,:]
# Append that entire instance to fold
fold2.loc[len(fold2)] = new_row
# Increase the counter by 1
counter += 1
# Allocate instance to fold3
elif counter == 3:
# Extract data for the new row
new_row = instances.iloc[row,:]
# Append that entire instance to fold
fold3.loc[len(fold3)] = new_row
# Increase the counter by 1
counter += 1
# Allocate instance to fold4
else:
# Extract data for the new row
new_row = instances.iloc[row,:]
# Append that entire instance to fold
fold4.loc[len(fold4)] = new_row
# Reset counter to 0
counter = 0
return fold0, fold1, fold2, fold3, fold4
Output Statistics of Naive Bayes
Here are the trace runs:
Here are the results:
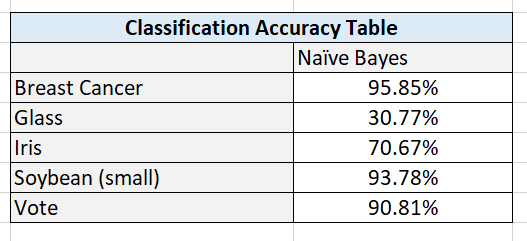
Here are the test statistics for each data set:
References
Alpaydin, E. (2014). Introduction to Machine Learning. Cambridge, Massachusetts: The MIT Press.
Fisher, R. (1988, July 01). Iris Data Set. Retrieved from Machine Learning Repository: https://archive.ics.uci.edu/ml/datasets/iris
German, B. (1987, September 1). Glass Identification Data Set. Retrieved from UCI Machine Learning Repository: https://archive.ics.uci.edu/ml/datasets/Glass+Identification
Kelleher, J. D., Namee, B., & Arcy, A. (2015). Fundamentals of Machine Learning for Predictive Data Analytics. Cambridge, Massachusetts: The MIT Press.
Michalski, R. (1980). Learning by being told and learning from examples: an experimental comparison of the two methodes of knowledge acquisition in the context of developing an expert system for soybean disease diagnosis. International Journal of Policy Analysis and Information Systems, 4(2), 125-161.
Rebala, G., Ravi, A., & Churiwala, S. (2019). An Introduction to Machine Learning. Switzerland: Springer.
Schlimmer, J. (1987, 04 27). Congressional Voting Records Data Set. Retrieved from Machine Learning Repository: https://archive.ics.uci.edu/ml/datasets/Congressional+Voting+Records
Wolberg, W. (1992, 07 15). Breast Cancer Wisconsin (Original) Data Set. Retrieved from Machine Learning Repository: https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+%28Original%25
Y. Ng, A., & Jordan, M. (2001). On Discriminative vs. Generative Classifiers: A Comparison of Logistic Regression and Naive Bayes. NIPS’01 Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic , 841-848.