In a lot of my machine learning projects, you might have noticed that I use a technique called five-fold stratified cross-validation. The purpose of cross-validation is to test the effectiveness of a machine learning algorithm. You don’t just want to spend all that time building your model only to find out that it only works well on the training data but works terribly on data it has never seen before. Cross-validation is the process that helps combat that risk.
The basic idea is that you shuffle your data randomly and then divide it into five equally-sized subsets. Ideally, you would like to have the same number of instances to be in each class in each of the five partitions.
For example, if you have a data set of 100 points where 1/3 of the data is in one class and 2/3 of the data is in another class, you will create five partitions of 20 instances each. Then for each of these partitions, 1/3 of the instances (~6 or 7 points) should be from the one class, and the remaining points should be in the other class. This is the “stratified” part of five-fold stratified cross-validation.
You then run five experiments where you train on four of the partitions (80% of the data) and test on the remaining partition (20% of the data). You rotate through the partitions so that each one serves as a test set exactly once. Then you average the performance on the five experiments when you report the results.
Let’s take a look at this process visually:
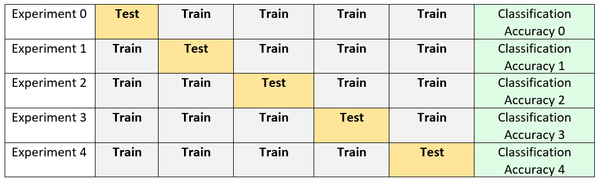
- Divide the data set into five random groups of equal size. Make sure that the proportion of each class in each group is roughly equal to its proportion in the entire data set.
- Use four groups for training and one group for testing.
- Calculate the classification accuracy.
- Repeat the procedure four more times, rotating the test set so that each group serves as a test set exactly once.
- Compute the average classification accuracy (or mean squared error) for the five runs.
Note that, if the target variable is continuous instead of a class, we use mean squared error instead of classification accuracy as the loss function.
Implementation 1 (Using Numpy in Python)
Here is the code for five-fold stratified cross-validation using the Numpy Python library. Just copy and paste it into your favorite IDE. Don’t be scared at how long the code is. I include a lot of comments so that you know what is going on.
import numpy as np # Import Numpy library
# File name: five_fold_stratified_cv.py
# Author: Addison Sears-Collins
# Date created: 6/20/2019
# Python version: 3.7
# Description: Implementation of five-fold stratified cross-validation
# Divide the data set into five random groups. Make sure
# that the proportion of each class in each group is roughly equal to its
# proportion in the entire data set.
# Required Data Set Format for Disrete Class Values
# Classification:
# Must be all numerical
# Columns (0 through N)
# 0: Instance ID
# 1: Attribute 1
# 2: Attribute 2
# 3: Attribute 3
# ...
# N: Actual Class
# Required Data Set Format for Continuous Class Values:
# Regression:
# Must be all numerical
# Columns (0 through N)
# 0: Instance ID
# 1: Attribute 1
# 2: Attribute 2
# 3: Attribute 3
# ...
# N: Actual Class
# N + 1: Stratification Bin
class FiveFoldStratCv:
# Constructor
# Parameters:
# np_dataset: The entire original data set as a numpy array
# problem_type: 'r' for regression and 'c' for classification
def __init__(self, np_dataset, problem_type):
self.__np_dataset = np_dataset
self.__problem_type = problem_type
# Returns:
# fold0, fold1, fold2, fold3, fold4
# Five folds whose class frequency distributions are
# each representative of the entire original data set (i.e. Five-Fold
# Stratified Cross Validation)
def get_five_folds(self):
# Record the number of columns in the data set
no_of_columns = np.size(self.__np_dataset,1)
# Record the number of rows in the data set
no_of_rows = np.size(self.__np_dataset,0)
# Create five empty folds (i.e. numpy arrays: fold0 through fold4)
fold0 = np.arange(1)
fold1 = np.arange(1)
fold2 = np.arange(1)
fold3 = np.arange(1)
fold4 = np.arange(1)
# Shuffle the data set randomly
np.random.shuffle(self.__np_dataset)
# Generate folds for classification problem
if self.__problem_type == "c":
# Record the column of the Actual Class
actual_class_column = no_of_columns - 1
# Generate an array containing the unique
# Actual Class values
unique_class_arr = np.unique(self.__np_dataset[
:,actual_class_column])
unique_class_arr_size = unique_class_arr.size
# For each unique class in the unique Actual Class array
for unique_class_arr_idx in range(0, unique_class_arr_size):
# Initialize the counter to 0
counter = 0
# Go through each row of the data set and find instances that
# are part of this unique class. Distribute them among one
# of five folds
for row in range(0, no_of_rows):
# If the value of the unique class is equal to the actual
# class in the original data set on this row
if unique_class_arr[unique_class_arr_idx] == (
self.__np_dataset[row,actual_class_column]):
# Allocate instance to fold0
if counter == 0:
# If fold has not yet been created
if np.size(fold0) == 1:
fold0 = self.__np_dataset[row,:]
# Increase the counter by 1
counter += 1
# Append this instance to the fold
else:
# Extract data for the new row
new_row = self.__np_dataset[row,:]
# Append that entire instance to fold
fold0 = np.vstack([fold0,new_row])
# Increase the counter by 1
counter += 1
# Allocate instance to fold1
elif counter == 1:
# If fold has not yet been created
if np.size(fold1) == 1:
fold1 = self.__np_dataset[row,:]
# Increase the counter by 1
counter += 1
# Append this instance to the fold
else:
# Extract data for the new row
new_row = self.__np_dataset[row,:]
# Append that entire instance to fold
fold1 = np.vstack([fold1,new_row])
# Increase the counter by 1
counter += 1
# Allocate instance to fold2
elif counter == 2:
# If fold has not yet been created
if np.size(fold2) == 1:
fold2 = self.__np_dataset[row,:]
# Increase the counter by 1
counter += 1
# Append this instance to the fold
else:
# Extract data for the new row
new_row = self.__np_dataset[row,:]
# Append that entire instance to fold
fold2 = np.vstack([fold2,new_row])
# Increase the counter by 1
counter += 1
# Allocate instance to fold3
elif counter == 3:
# If fold has not yet been created
if np.size(fold3) == 1:
fold3 = self.__np_dataset[row,:]
# Increase the counter by 1
counter += 1
# Append this instance to the fold
else:
# Extract data for the new row
new_row = self.__np_dataset[row,:]
# Append that entire instance to fold
fold3 = np.vstack([fold3,new_row])
# Increase the counter by 1
counter += 1
# Allocate instance to fold4
else:
# If fold has not yet been created
if np.size(fold4) == 1:
fold4 = self.__np_dataset[row,:]
# Reset counter to 0
counter = 0
# Append this instance to the fold
else:
# Extract data for the new row
new_row = self.__np_dataset[row,:]
# Append that entire instance to fold
fold4 = np.vstack([fold4,new_row])
# Reset counter to 0
counter = 0
# If this is a regression problem
else:
# Record the column of the Stratification Bin
strat_bin_column = no_of_columns - 1
# Generate an array containing the unique
# Stratification Bin values
unique_bin_arr = np.unique(self.__np_dataset[
:,strat_bin_column])
unique_bin_arr_size = unique_bin_arr.size
# For each unique bin in the unique Stratification Bin array
for unique_bin_arr_idx in range(0, unique_bin_arr_size):
# Initialize the counter to 0
counter = 0
# Go through each row of the data set and find instances that
# are part of this unique bin. Distribute them among one
# of five folds
for row in range(0, no_of_rows):
# If the value of the unique bin is equal to the actual
# bin in the original data set on this row
if unique_bin_arr[unique_bin_arr_idx] == (
self.__np_dataset[row,strat_bin_column]):
# Allocate instance to fold0
if counter == 0:
# If fold has not yet been created
if np.size(fold0) == 1:
fold0 = self.__np_dataset[row,:]
# Increase the counter by 1
counter += 1
# Append this instance to the fold
else:
# Extract data for the new row
new_row = self.__np_dataset[row,:]
# Append that entire instance to fold
fold0 = np.vstack([fold0,new_row])
# Increase the counter by 1
counter += 1
# Allocate instance to fold1
elif counter == 1:
# If fold has not yet been created
if np.size(fold1) == 1:
fold1 = self.__np_dataset[row,:]
# Increase the counter by 1
counter += 1
# Append this instance to the fold
else:
# Extract data for the new row
new_row = self.__np_dataset[row,:]
# Append that entire instance to fold
fold1 = np.vstack([fold1,new_row])
# Increase the counter by 1
counter += 1
# Allocate instance to fold2
elif counter == 2:
# If fold has not yet been created
if np.size(fold2) == 1:
fold2 = self.__np_dataset[row,:]
# Increase the counter by 1
counter += 1
# Append this instance to the fold
else:
# Extract data for the new row
new_row = self.__np_dataset[row,:]
# Append that entire instance to fold
fold2 = np.vstack([fold2,new_row])
# Increase the counter by 1
counter += 1
# Allocate instance to fold3
elif counter == 3:
# If fold has not yet been created
if np.size(fold3) == 1:
fold3 = self.__np_dataset[row,:]
# Increase the counter by 1
counter += 1
# Append this instance to the fold
else:
# Extract data for the new row
new_row = self.__np_dataset[row,:]
# Append that entire instance to fold
fold3 = np.vstack([fold3,new_row])
# Increase the counter by 1
counter += 1
# Allocate instance to fold4
else:
# If fold has not yet been created
if np.size(fold4) == 1:
fold4 = self.__np_dataset[row,:]
# Reset counter to 0
counter = 0
# Append this instance to the fold
else:
# Extract data for the new row
new_row = self.__np_dataset[row,:]
# Append that entire instance to fold
fold4 = np.vstack([fold4,new_row])
# Reset counter to 0
counter = 0
return fold0, fold1, fold2, fold3, fold4
Implementation 2 (Using the Counter subclass)
Here is another implementation using the Counter subclass.
import random
from collections import Counter # Used for counting
# File name: five_fold_stratified_cv.py
# Author: Addison Sears-Collins
# Date created: 7/7/2019
# Python version: 3.7
# Description: Implementation of five-fold stratified cross-validation
# Divide the data set into five random groups. Make sure
# that the proportion of each class in each group is roughly equal to its
# proportion in the entire data set.
# Required Data Set Format for Classification Problems:
# Columns (0 through N)
# 0: Class
# 1: Attribute 1
# 2: Attribute 2
# 3: Attribute 3
# ...
# N: Attribute N
def get_five_folds(instances):
"""
Parameters:
instances: A list of dictionaries where each dictionary is an instance.
Each dictionary contains attribute:value pairs
Returns:
fold0, fold1, fold2, fold3, fold4
Five folds whose class frequency distributions are
each representative of the entire original data set (i.e. Five-Fold
Stratified Cross Validation)
"""
# Create five empty folds
fold0 = []
fold1 = []
fold2 = []
fold3 = []
fold4 = []
# Shuffle the data randomly
random.shuffle(instances)
# Generate a list of the unique class values and their counts
classes = [] # Create an empty list named 'classes'
# For each instance in the list of instances, append the value of the class
# to the end of the classes list
for instance in instances:
classes.append(instance['Class'])
# Create a list of the unique classes
unique_classes = list(Counter(classes).keys())
# For each unique class in the unique class list
for uniqueclass in unique_classes:
# Initialize the counter to 0
counter = 0
# Go through each instance of the data set and find instances that
# are part of this unique class. Distribute them among one
# of five folds
for instance in instances:
# If we have a match
if uniqueclass == instance['Class']:
# Allocate instance to fold0
if counter == 0:
# Append this instance to the fold
fold0.append(instance)
# Increase the counter by 1
counter += 1
# Allocate instance to fold1
elif counter == 1:
# Append this instance to the fold
fold1.append(instance)
# Increase the counter by 1
counter += 1
# Allocate instance to fold2
elif counter == 2:
# Append this instance to the fold
fold2.append(instance)
# Increase the counter by 1
counter += 1
# Allocate instance to fold3
elif counter == 3:
# Append this instance to the fold
fold3.append(instance)
# Increase the counter by 1
counter += 1
# Allocate instance to fold4
else:
# Append this instance to the fold
fold4.append(instance)
# Reset the counter to 0
counter = 0
# Shuffle the folds
random.shuffle(fold0)
random.shuffle(fold1)
random.shuffle(fold2)
random.shuffle(fold3)
random.shuffle(fold4)
# Return the folds
return fold0, fold1, fold2, fold3, fold4

