How To Set up a ROS2 Project for Python – Foxy Fitzroy

In this tutorial, we will learn how to set up a ROS2 project from scratch.

Prerequisites

You have ROS2 installed and working in a Linux environment.

Source Your ROS2 Installation

We first need to create a new workspace. A workspace is a folder that will contain all your ROS packages.

Here is the official tutorial, but I’ll walk through all the steps below.

Open a new terminal window.

To find out which version of ROS2 you have installed, type the following command:

printenv ROS_DISTRO

I’m using the foxy distribution of ROS2.

Now, let’s source the ROS2 environment. Type the following command:

source /opt/ros/foxy/setup.bash

Create a Workspace

Let’s create a workspace directory. “-p” is short for “–parents”. This flag makes sure the mkdir (“make directory”) command makes the parent /dev_ws/ folder as well as the /src/ folder within it (Feel free to check out my Linux commands tutorial).

mkdir -p ~/dev_ws/src

cd ~/dev_ws/src

The syntax is:

mkdir -p ~/<yourworkspace>_ws/src

cd ~/<yourworkspace>_ws/src

Create a Package

Now let’s create a ROS package.

We will use the following syntax.

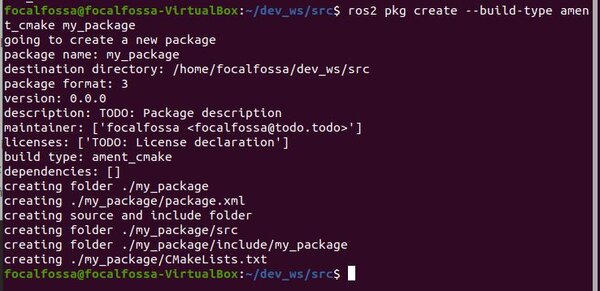
ros2 pkg create –build-type ament_python <package_name>

Type this command:

ros2 pkg create --build-type ament_python my_package

Your package named my_package has now been created.

Build Your Package

Return to the root of your workspace:

cd ~/dev_ws

Build all packages in the workspace.

colcon build

If you only want to build my_package, you can type

colcon build --packages-select my_package

Source the Setup File

Open a new terminal window.

Source your ROS2 installation.

source /opt/ros/foxy/setup.bash

Move to your workspace folder.

cd ~/dev_ws

Add the files you just created to the path.

source install/setup.bash

If you don’t have gedit installed, install it using this command:

sudo apt-get install gedit

Open your .bashrc file.

gedit ~/.bashrc

Add this line of code to the very bottom of the file.

source /opt/ros/foxy/setup.bash

You now don’t have to source your ROS2 installation every time you open a new terminal window.

While you’re at it add this line of code to the very bottom of the .bashrc file.

source ~/dev_ws/install/setup.bash

The syntax is

source ~/<your_workspace>/install/setup.bash

Save the file, and close it.

Your system now knows where to find your ROS2 packages.

Write Node(s)

Move to the dev_ws/src/my_package/my_package folder.

cd dev_ws/src/my_package/my_package

Write a Python program (i.e. node), and add it to this folder you’re currently in. This post has some sample code you can use. Copy the Publisher Node code, and paste it into a file named my_python_script.py.

gedit my_python_script.py

Save the file and close it.

Now change the permissions on the file.

chmod +x my_python_script.py

Make sure that the names of your python nodes are not the same as the name of the package. Otherwise, you will have ImportErrors.

You can add as many Python programs as you like. For example, you might have one node that defines a class, and then you have another node that imports that class and uses it to make calculations, which are then published to a ROS2 topic as some data type (e.g. Float64, geometry_msgs/Twist, etc.).

Add Dependencies

Navigate one level back.

cd ..

You are now in the dev_ws/src/my_package/ directory.

Type

ls

You should see the setup.py, setup.cfg, and package.xml files.

Open package.xml with your text editor.

gedit package.xml

Fill in the <description>, <maintainer>, and <license> tags.

Add a new line after the ament_python build_type dependency and add the following dependencies which will correspond to other packages the packages in this workspace needs (this will be in your node’s import statements):

<exec_depend>rclpy</exec_depend>

<exec_depend>geometry_msgs</exec_depend>

This let’s the system know that this package needs the rclpy and geometry_msgs packages when its code is executed.

The code doesn’t need the geometry_msgs package, but I’m having you add it anyway just to show you that you can add all sorts of message types in this package.xml file.

Save the file.

Add an Entry Point

Now we need to add the entry points for the node(s) by opening the setup.py file.

gedit setup.py

Make sure this code is in there:

entry_points={
        'console_scripts': [
                'my_python_script = my_package.my_python_script:main',
        ],
},

The syntax is:

‘my_python_script = my_package.my_python_script:main’

my_python_script will be the name of the executable.

‘my_package.my_python_script:main’ tells the system to execute the main() function inside my_python_script.py. Therefore, this will be the entry point when you run your node.

The executable script will go to:

~/dev_ws/install/my_package/lib/my_package/

Save setup.py and close it.

Check for Missing Dependencies

Check for any missing dependencies before you build the package.

Move to your workspace folder.

cd ~/dev_ws

Run the following command:

rosdep install -i --from-path src --rosdistro <distro> -y

For example:

rosdep install -i --from-path src --rosdistro foxy -y

I get a message that says:

“#All required rosdeps installed successfully”

Build and Run

Now, build your package by first moving to the src folder.

cd src

Then build the package.

colcon build --packages-select my_package

You should get a message that says:

“Summary: 1 package finished [<time it took in seconds>]”

Open a new terminal tab.

cd ~/dev_ws

Run the node:

ros2 run my_package my_python_script

The syntax is:

ros2 run <package_name> <node name without the .py>

Open a new terminal tab, and move to the root directory of the workspace.

cd ~/dev_ws

List the active topics.

ros2 topic list -t

To listen to any topic, type:

ros2 topic echo /topic_name

Where you replace “/topic_name” with the name of the topic.

When you’ve had enough, type Ctrl+C in each terminal tab to stop the nodes from spinning.

Zip the Workspace for Distribution

If you ever want to zip the whole workspace and send it to someone, open a new terminal window.

Move to the directory containing your workspace.

cd ~/dev_ws

cd ..

zip -r myros2workspace.zip /dev_ws

The syntax is:

zip -r <filename.zip> <foldername>

How To Multiply Two Quaternions Together Using Python

Here is how we multiply two quaternions together using Python. Multiplying two quaternions together has the effect of performing one rotation around an axis and then performing another rotation about around an axis.

import numpy as np
import random

def quaternion_multiply(Q0,Q1):
    """
    Multiplies two quaternions.

    Input
    :param Q0: A 4 element array containing the first quaternion (q01,q11,q21,q31) 
    :param Q1: A 4 element array containing the second quaternion (q02,q12,q22,q32) 

    Output
    :return: A 4 element array containing the final quaternion (q03,q13,q23,q33) 

    """
    # Extract the values from Q0
    w0 = Q0[0]
    x0 = Q0[1]
    y0 = Q0[2]
    z0 = Q0[3]
	
    # Extract the values from Q1
    w1 = Q1[0]
    x1 = Q1[1]
    y1 = Q1[2]
    z1 = Q1[3]
	
    # Computer the product of the two quaternions, term by term
    Q0Q1_w = w0 * w1 - x0 * x1 - y0 * y1 - z0 * z1
    Q0Q1_x = w0 * x1 + x0 * w1 + y0 * z1 - z0 * y1
    Q0Q1_y = w0 * y1 - x0 * z1 + y0 * w1 + z0 * x1
    Q0Q1_z = w0 * z1 + x0 * y1 - y0 * x1 + z0 * w1
	
    # Create a 4 element array containing the final quaternion
    final_quaternion = np.array([Q0Q1_w, Q0Q1_x, Q0Q1_y, Q0Q1_z])
	
    # Return a 4 element array containing the final quaternion (q02,q12,q22,q32) 
    return final_quaternion
    
Q0 = np.random.rand(4) # First quaternion
Q1 = np.random.rand(4) # Second quaternion
Q = quaternion_multiply(Q0, Q1)
print("{0} x {1} = {2}".format(Q0, Q1, Q))

How to Convert a Quaternion to a Rotation Matrix

In this tutorial, I’ll show you how to convert a quaternion to a three-dimensional rotation matrix. At the end of this post, I have provided the Python code to perform the conversion.

What is a Quaternion?

A quaternion is one of several mathematical ways to represent the orientation and rotation of an object in three dimensions. Another way is to use Euler angle-based rotation matrices like I did on this post and this post (i.e. roll, pitch, and yaw), as well as the cover image of this tutorial.

Quaternions are often used instead of Euler angle rotation matrices because “compared to rotation matrices they are more compact, more numerically stable, and more efficient” (Source: Wikipedia).

Note that a quaternion describes just the rotation of a coordinate frame (i.e. some object in 3D space) about an arbitrary axis, but it doesn’t tell you anything about that object’s position.

The Use of Quaternions in Robotics

Quaternions are the default method of representing orientations and rotations in ROS, the most popular platform for robotics software development.

In robotics, we are always trying to rotate stuff. For example, we might observe an object in a camera. In order to get a robotic arm to grab the object, we need to rotate the camera reference frame to the robot reference frame so that the robot “knows” the location of the object in its own coordinate frame.

Once the rotation from camera pixel coordinates to robot base frame coordinates is complete, the robotic arm can then move its motors to the appropriate angles to pick up the object.

How to Represent Quaternions

Quaternions are an extension of complex numbers. However instead of two values (e.g. a + bi or x + yi…same thing) that represent a point (or vector), we have four values (a, b, c, d):

q = a + bi + cj + dk

The four values in a quaternion consist of one scalar and a 3-element unit vector.

Instead of a, b, c, and d, you will commonly see:

q = w + xi + yj + zk or q = q₀ + q₁i + q₂j + q₃k

q₀ is a scalar value that represents an angle of rotation
q₁, q₂, and q₃ correspond to an axis of rotation about which the angle of rotation is performed.

Other ways you can write a quaternion are as follows:

q = (q₀, q₁, q₂, q₃)
q = (q₀, q) = q₀ + q

The cool thing about quaternions is they work just like complex numbers. In two dimensions, you can rotate a vector using complex number multiplication. You can do the same with quaternions. The math is more complicated with four terms instead of two, but the principle is the same.

Let’s take a look at a two-dimensional example of complex number multiplication so that you can understand the concept of multiplying imaginary (complex) numbers to rotate a vector. Quaternions add a couple more variables to extend this concept to represent rotation in the 3D space.

2D Example

Suppose we have a vector on a 2D plane with the following specifications:

(x = 3, y = 1)

This vector can be represented in complex numbers as:

3 + i  (e.g. using the x +yi form of complex numbers)

Let’s rotate this vector 45 degrees (which is π/4 in radians).

To rotate 45 degrees, we multiply the number by:

cos(π/4) + sin(π/4)i (De Moivre’s formula)

So, we have sqrt means (“take the square root of”):

(1/sqrt(2)+ i/sqrt(2)) * (3 + i) = sqrt(2) + 2sqrt(2)i

And since:

sqrt(2) = 1.414

our new vector is:

(x = 1.414, y = 4.242)

As I mentioned earlier, the math for multiplying real quaternions together is more complex than this, but the principle is the same. Multiply an orientation (represented as a quaternion) by a rotation (represented as a quaternion) to get the new orientation.

Convert a Quaternion to a Rotation Matrix

Given a quaternion, you can find the corresponding three dimensional rotation matrix using the following formula.

quaternion-to-rotation-matrix — Source: Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace and Virtual Reality by J. B. Kuipers (Chapter 5, Section 5.14 “Quaternions to Matrices”, pg. 125)

Python Code

In Python code, we have:

import numpy as np

def quaternion_rotation_matrix(Q):
    """
    Covert a quaternion into a full three-dimensional rotation matrix.

    Input
    :param Q: A 4 element array representing the quaternion (q0,q1,q2,q3) 

    Output
    :return: A 3x3 element matrix representing the full 3D rotation matrix. 
             This rotation matrix converts a point in the local reference 
             frame to a point in the global reference frame.
    """
    # Extract the values from Q
    q0 = Q[0]
    q1 = Q[1]
    q2 = Q[2]
    q3 = Q[3]
	
    # First row of the rotation matrix
    r00 = 2 * (q0 * q0 + q1 * q1) - 1
    r01 = 2 * (q1 * q2 - q0 * q3)
    r02 = 2 * (q1 * q3 + q0 * q2)
	
    # Second row of the rotation matrix
    r10 = 2 * (q1 * q2 + q0 * q3)
    r11 = 2 * (q0 * q0 + q2 * q2) - 1
    r12 = 2 * (q2 * q3 - q0 * q1)
	
    # Third row of the rotation matrix
    r20 = 2 * (q1 * q3 - q0 * q2)
    r21 = 2 * (q2 * q3 + q0 * q1)
    r22 = 2 * (q0 * q0 + q3 * q3) - 1
	
    # 3x3 rotation matrix
    rot_matrix = np.array([[r00, r01, r02],
                           [r10, r11, r12],
                           [r20, r21, r22]])
						   
    return rot_matrix