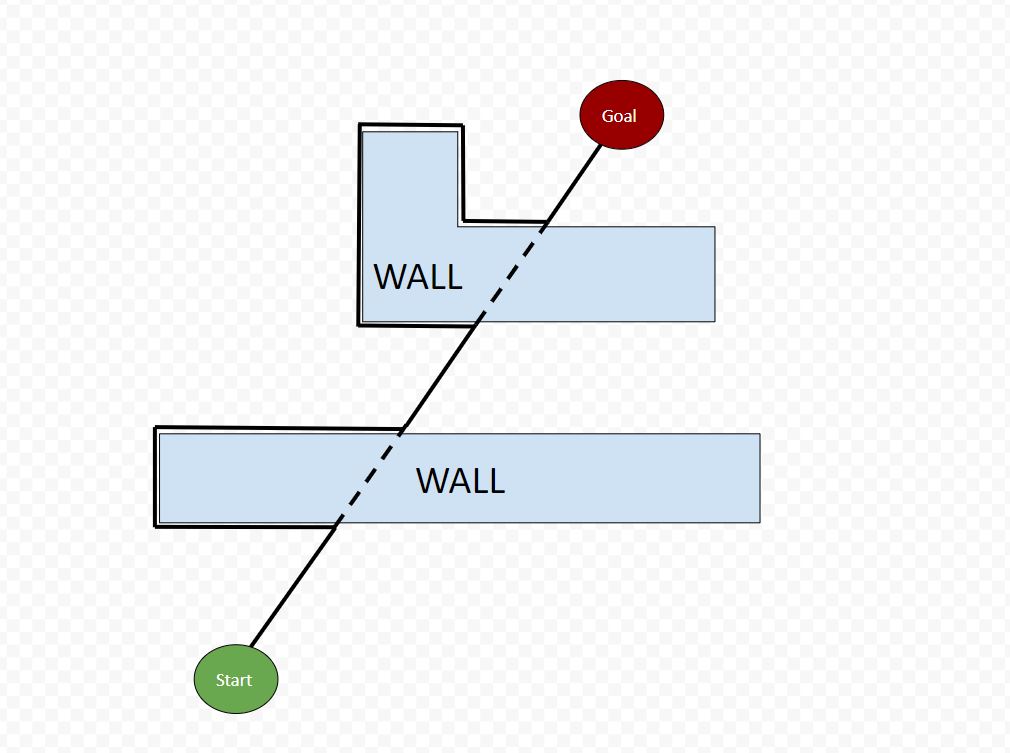
In this tutorial, we will learn about the Bug2 algorithm for robot motion planning. The Bug2 algorithm is used when you have a mobile robot:
- With a known starting location
- With a known goal location
- Inside an unexplored environment
- Contains a distance sensor that can detect the distances to objects and walls in the environment (e.g. like an ultrasonic sensor or a laser distance sensor.)
- Contains an encoder that the robot can use to estimate how far the robot has traveled from the starting location.
Here is a video of a simulated robot I developed in Gazebo and ROS2 that uses the Bug2 algorithm to move from a starting point to a goal point, avoiding walls along the way.
Real-World Applications
Imagine an automatic vacuum cleaner like the one below. It vacuums a room and then needs to move autonomously to another room so that it can clean that room. Along the way, the robot must avoid bumping into walls.

Algorithm Description
On a high level, the Bug2 algorithm has two main modes:
- Go to Goal Mode: Move from the current location towards the goal (x,y) coordinate.
- Wall Following Mode: Move along a wall.
Here is pseudocode for the algorithm:
1. Calculate a start-goal line. The start-goal line is an imaginary line that connects the starting position to the goal position.
2. While Not at the Goal
- Move towards the goal along the start-goal line.
- If a wall is encountered:
- Remember the location where the wall was first encountered. This is the “hit point.”
- Follow the wall until you encounter the start-goal line. This point is known as the “leave point.”
- If the leave point is closer to the goal than the hit point, leave the wall, and move towards the goal again.
- Otherwise, continue following the wall.
- If a wall is encountered:
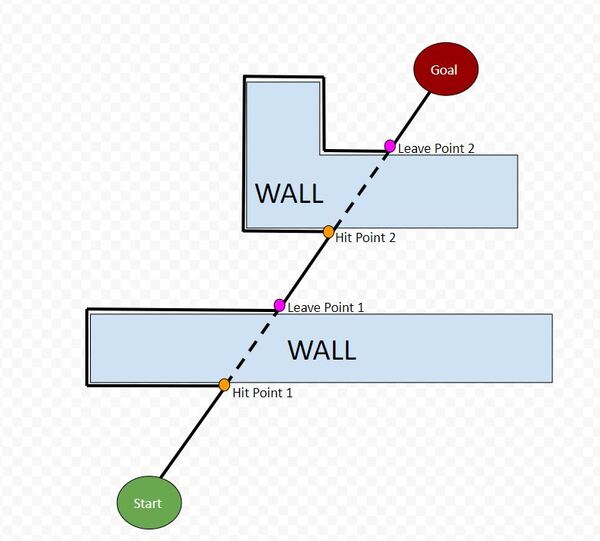
That’s the algorithm. In the image below, I have labeled the hit points and leave points.
Python Implementation (ROS2)
The robot you see in the video at the beginning of this tutorial has a laser distance scanner mounted on top of it that enables it to detect distances from 0 degrees (right side of the robot) to 180 degrees (left side of the robot). It is using three Python functions, bug2, follow_wall, and go_to_goal.
Below is my complete code. It runs in ROS2 Foxy Fitzroy and Gazebo and makes use of the Differential Drive plugin.
Since we’re just focusing on the algorithms in this post, I won’t go into the details of how I created the robot, built the simulated maze, and created publisher and subscriber nodes for the goal locations, robot pose, and laser distance sensor information (I might cover this in a future post).
Don’t be intimidated by the code. It is long but well-commented. Go through each piece and function one step at a time. Focus only on the following three methods:
- go_to_goal(self) method
- follow_wall(self) method
- bug2(self) method
Those three methods encapsulate the implementation of Bug2.
I created descriptive variable names so that you can compare the code to the pseudocode I wrote earlier in this tutorial.
# Author: Addison Sears-Collins
# Date: December 17, 2020
# ROS Version: ROS 2 Foxy Fitzroy
############## IMPORT LIBRARIES #################
# Python math library
import math
# ROS client library for Python
import rclpy
# Enables pauses in the execution of code
from time import sleep
# Used to create nodes
from rclpy.node import Node
# Enables the use of the string message type
from std_msgs.msg import String
# Twist is linear and angular velocity
from geometry_msgs.msg import Twist
# Handles LaserScan messages to sense distance to obstacles (i.e. walls)
from sensor_msgs.msg import LaserScan
# Handle Pose messages
from geometry_msgs.msg import Pose
# Handle float64 arrays
from std_msgs.msg import Float64MultiArray
# Handles quality of service for LaserScan data
from rclpy.qos import qos_profile_sensor_data
# Scientific computing library
import numpy as np
class PlaceholderController(Node):
"""
Create a Placeholder Controller class, which is a subclass of the Node
class for ROS2.
"""
def __init__(self):
"""
Class constructor to set up the node
"""
####### INITIALIZE ROS PUBLISHERS AND SUBSCRIBERS##############
# Initiate the Node class's constructor and give it a name
super().__init__('PlaceholderController')
# Create a subscriber
# This node subscribes to messages of type Float64MultiArray
# over a topic named: /en613/state_est
# The message represents the current estimated state:
# [x, y, yaw]
# The callback function is called as soon as a message
# is received.
# The maximum number of queued messages is 10.
self.subscription = self.create_subscription(
Float64MultiArray,
'/en613/state_est',
self.state_estimate_callback,
10)
self.subscription # prevent unused variable warning
# Create a subscriber
# This node subscribes to messages of type
# sensor_msgs/LaserScan
self.scan_subscriber = self.create_subscription(
LaserScan,
'/en613/scan',
self.scan_callback,
qos_profile=qos_profile_sensor_data)
# Create a subscriber
# This node subscribes to messages of type geometry_msgs/Pose
# over a topic named: /en613/goal
# The message represents the the goal position.
# The callback function is called as soon as a message
# is received.
# The maximum number of queued messages is 10.
self.subscription_goal_pose = self.create_subscription(
Pose,
'/en613/goal',
self.pose_received,
10)
# Create a publisher
# This node publishes the desired linear and angular velocity
# of the robot (in the robot chassis coordinate frame) to the
# /en613/cmd_vel topic. Using the diff_drive
# plugin enables the basic_robot model to read this
# /end613/cmd_vel topic and execute the motion accordingly.
self.publisher_ = self.create_publisher(
Twist,
'/en613/cmd_vel',
10)
# Initialize the LaserScan sensor readings to some large value
# Values are in meters.
self.left_dist = 999999.9 # Left
self.leftfront_dist = 999999.9 # Left-front
self.front_dist = 999999.9 # Front
self.rightfront_dist = 999999.9 # Right-front
self.right_dist = 999999.9 # Right
################### ROBOT CONTROL PARAMETERS ##################
# Maximum forward speed of the robot in meters per second
# Any faster than this and the robot risks falling over.
self.forward_speed = 0.035
# Current position and orientation of the robot in the global
# reference frame
self.current_x = 0.0
self.current_y = 0.0
self.current_yaw = 0.0
# By changing the value of self.robot_mode, you can alter what
# the robot will do when the program is launched.
# "obstacle avoidance mode": Robot will avoid obstacles
# "go to goal mode": Robot will head to an x,y coordinate
# "wall following mode": Robot will follow a wall
self.robot_mode = "go to goal mode"
############# OBSTACLE AVOIDANCE MODE PARAMETERS ##############
# Obstacle detection distance threshold
self.dist_thresh_obs = 0.25 # in meters
# Maximum left-turning speed
self.turning_speed = 0.25 # rad/s
############# GO TO GOAL MODE PARAMETERS ######################
# Finite states for the go to goal mode
# "adjust heading": Orient towards a goal x, y coordinate
# "go straight": Go straight towards goal x, y coordinate
# "goal achieved": Reached goal x, y coordinate
self.go_to_goal_state = "adjust heading"
# List the goal destinations
# We create a list of the (x,y) coordinate goals
self.goal_x_coordinates = False # [ 0.0, 3.0, 0.0, -1.5, -1.5, 4.5, 0.0]
self.goal_y_coordinates = False # [-4.0, 1.0, 1.5, 1.0, -3.0, -4.0, 0.0]
# Keep track of which goal we're headed towards
self.goal_idx = 0
# Keep track of when we've reached the end of the goal list
self.goal_max_idx = None # len(self.goal_x_coordinates) - 1
# +/- 2.0 degrees of precision
self.yaw_precision = 2.0 * (math.pi / 180)
# How quickly we need to turn when we need to make a heading
# adjustment (rad/s)
self.turning_speed_yaw_adjustment = 0.0625
# Need to get within +/- 0.2 meter (20 cm) of (x,y) goal
self.dist_precision = 0.2
############# WALL FOLLOWING MODE PARAMETERS ##################
# Finite states for the wall following mode
# "turn left": Robot turns towards the left
# "search for wall": Robot tries to locate the wall
# "follow wall": Robot moves parallel to the wall
self.wall_following_state = "turn left"
# Set turning speeds (to the left) in rad/s
# These values were determined by trial and error.
self.turning_speed_wf_fast = 1.0 # Fast turn
self.turning_speed_wf_slow = 0.125 # Slow turn
# Wall following distance threshold.
# We want to try to keep within this distance from the wall.
self.dist_thresh_wf = 0.45 # in meters
# We don't want to get too close to the wall though.
self.dist_too_close_to_wall = 0.15 # in meters
################### BUG2 PARAMETERS ###########################
# Bug2 Algorithm Switch
# Can turn "ON" or "OFF" depending on if you want to run Bug2
# Motion Planning Algorithm
self.bug2_switch = "ON"
# Start-Goal Line Calculated?
self.start_goal_line_calculated = False
# Start-Goal Line Parameters
self.start_goal_line_slope_m = 0
self.start_goal_line_y_intercept = 0
self.start_goal_line_xstart = 0
self.start_goal_line_xgoal = 0
self.start_goal_line_ystart = 0
self.start_goal_line_ygoal = 0
# Anything less than this distance means we have encountered
# a wall. Value determined through trial and error.
self.dist_thresh_bug2 = 0.15
# Leave point must be within +/- 0.1m of the start-goal line
# in order to go from wall following mode to go to goal mode
self.distance_to_start_goal_line_precision = 0.1
# Used to record the (x,y) coordinate where the robot hit
# a wall.
self.hit_point_x = 0
self.hit_point_y = 0
# Distance between the hit point and the goal in meters
self.distance_to_goal_from_hit_point = 0.0
# Used to record the (x,y) coordinate where the robot left
# a wall.
self.leave_point_x = 0
self.leave_point_y = 0
# Distance between the leave point and the goal in meters
self.distance_to_goal_from_leave_point = 0.0
# The hit point and leave point must be far enough
# apart to change state from wall following to go to goal
# This value helps prevent the robot from getting stuck and
# rotating in endless circles.
# This distance was determined through trial and error.
self.leave_point_to_hit_point_diff = 0.25 # in meters
def pose_received(self,msg):
"""
Populate the pose.
"""
self.goal_x_coordinates = [msg.position.x]
self.goal_y_coordinates = [msg.position.y]
self.goal_max_idx = len(self.goal_x_coordinates) - 1
def scan_callback(self, msg):
"""
This method gets called every time a LaserScan message is
received on the /en613/scan ROS topic
"""
# Read the laser scan data that indicates distances
# to obstacles (e.g. wall) in meters and extract
# 5 distinct laser readings to work with.
# Each reading is separated by 45 degrees.
# Assumes 181 laser readings, separated by 1 degree.
# (e.g. -90 degrees to 90 degrees....0 to 180 degrees)
self.left_dist = msg.ranges[180]
self.leftfront_dist = msg.ranges[135]
self.front_dist = msg.ranges[90]
self.rightfront_dist = msg.ranges[45]
self.right_dist = msg.ranges[0]
# The total number of laser rays. Used for testing.
#number_of_laser_rays = str(len(msg.ranges))
# Print the distance values (in meters) for testing
#self.get_logger().info('L:%f LF:%f F:%f RF:%f R:%f' % (
# self.left_dist,
# self.leftfront_dist,
# self.front_dist,
# self.rightfront_dist,
# self.right_dist))
if self.robot_mode == "obstacle avoidance mode":
self.avoid_obstacles()
def state_estimate_callback(self, msg):
"""
Extract the position and orientation data.
This callback is called each time
a new message is received on the '/en613/state_est' topic
"""
# Update the current estimated state in the global reference frame
curr_state = msg.data
self.current_x = curr_state[0]
self.current_y = curr_state[1]
self.current_yaw = curr_state[2]
# Wait until we have received some goal destinations.
if self.goal_x_coordinates == False and self.goal_y_coordinates == False:
return
# Print the pose of the robot
# Used for testing
#self.get_logger().info('X:%f Y:%f YAW:%f' % (
# self.current_x,
# self.current_y,
# np.rad2deg(self.current_yaw))) # Goes from -pi to pi
# See if the Bug2 algorithm is activated. If yes, call bug2()
if self.bug2_switch == "ON":
self.bug2()
else:
if self.robot_mode == "go to goal mode":
self.go_to_goal()
elif self.robot_mode == "wall following mode":
self.follow_wall()
else:
pass # Do nothing
def avoid_obstacles(self):
"""
Wander around the maze and avoid obstacles.
"""
# Create a Twist message and initialize all the values
# for the linear and angular velocities
msg = Twist()
msg.linear.x = 0.0
msg.linear.y = 0.0
msg.linear.z = 0.0
msg.angular.x = 0.0
msg.angular.y = 0.0
msg.angular.z = 0.0
# Logic for avoiding obstacles (e.g. walls)
# >d means no obstacle detected by that laser beam
# <d means an obstacle was detected by that laser beam
d = self.dist_thresh_obs
if self.leftfront_dist > d and self.front_dist > d and self.rightfront_dist > d:
msg.linear.x = self.forward_speed # Go straight forward
elif self.leftfront_dist > d and self.front_dist < d and self.rightfront_dist > d:
msg.angular.z = self.turning_speed # Turn left
elif self.leftfront_dist > d and self.front_dist > d and self.rightfront_dist < d:
msg.angular.z = self.turning_speed
elif self.leftfront_dist < d and self.front_dist > d and self.rightfront_dist > d:
msg.angular.z = -self.turning_speed # Turn right
elif self.leftfront_dist > d and self.front_dist < d and self.rightfront_dist < d:
msg.angular.z = self.turning_speed
elif self.leftfront_dist < d and self.front_dist < d and self.rightfront_dist > d:
msg.angular.z = -self.turning_speed
elif self.leftfront_dist < d and self.front_dist < d and self.rightfront_dist < d:
msg.angular.z = self.turning_speed
elif self.leftfront_dist < d and self.front_dist > d and self.rightfront_dist < d:
msg.linear.x = self.forward_speed
else:
pass
# Send the velocity commands to the robot by publishing
# to the topic
self.publisher_.publish(msg)
def go_to_goal(self):
"""
This code drives the robot towards to the goal destination
"""
# Create a geometry_msgs/Twist message
msg = Twist()
msg.linear.x = 0.0
msg.linear.y = 0.0
msg.linear.z = 0.0
msg.angular.x = 0.0
msg.angular.y = 0.0
msg.angular.z = 0.0
# If Bug2 algorithm is activated
if self.bug2_switch == "ON":
# If the wall is in the way
d = self.dist_thresh_bug2
if ( self.leftfront_dist < d or
self.front_dist < d or
self.rightfront_dist < d):
# Change the mode to wall following mode.
self.robot_mode = "wall following mode"
# Record the hit point
self.hit_point_x = self.current_x
self.hit_point_y = self.current_y
# Record the distance to the goal from the
# hit point
self.distance_to_goal_from_hit_point = (
math.sqrt((
pow(self.goal_x_coordinates[self.goal_idx] - self.hit_point_x, 2)) + (
pow(self.goal_y_coordinates[self.goal_idx] - self.hit_point_y, 2))))
# Make a hard left to begin following wall
msg.angular.z = self.turning_speed_wf_fast
# Send command to the robot
self.publisher_.publish(msg)
# Exit this function
return
# Fix the heading
if (self.go_to_goal_state == "adjust heading"):
# Calculate the desired heading based on the current position
# and the desired position
desired_yaw = math.atan2(
self.goal_y_coordinates[self.goal_idx] - self.current_y,
self.goal_x_coordinates[self.goal_idx] - self.current_x)
# How far off is the current heading in radians?
yaw_error = desired_yaw - self.current_yaw
# Adjust heading if heading is not good enough
if math.fabs(yaw_error) > self.yaw_precision:
if yaw_error > 0:
# Turn left (counterclockwise)
msg.angular.z = self.turning_speed_yaw_adjustment
else:
# Turn right (clockwise)
msg.angular.z = -self.turning_speed_yaw_adjustment
# Command the robot to adjust the heading
self.publisher_.publish(msg)
# Change the state if the heading is good enough
else:
# Change the state
self.go_to_goal_state = "go straight"
# Command the robot to stop turning
self.publisher_.publish(msg)
# Go straight
elif (self.go_to_goal_state == "go straight"):
position_error = math.sqrt(
pow(
self.goal_x_coordinates[self.goal_idx] - self.current_x, 2)
+ pow(
self.goal_y_coordinates[self.goal_idx] - self.current_y, 2))
# If we are still too far away from the goal
if position_error > self.dist_precision:
# Move straight ahead
msg.linear.x = self.forward_speed
# Command the robot to move
self.publisher_.publish(msg)
# Check our heading
desired_yaw = math.atan2(
self.goal_y_coordinates[self.goal_idx] - self.current_y,
self.goal_x_coordinates[self.goal_idx] - self.current_x)
# How far off is the heading?
yaw_error = desired_yaw - self.current_yaw
# Check the heading and change the state if there is too much heading error
if math.fabs(yaw_error) > self.yaw_precision:
# Change the state
self.go_to_goal_state = "adjust heading"
# We reached our goal. Change the state.
else:
# Change the state
self.go_to_goal_state = "goal achieved"
# Command the robot to stop
self.publisher_.publish(msg)
# Goal achieved
elif (self.go_to_goal_state == "goal achieved"):
self.get_logger().info('Goal achieved! X:%f Y:%f' % (
self.goal_x_coordinates[self.goal_idx],
self.goal_y_coordinates[self.goal_idx]))
# Get the next goal
self.goal_idx = self.goal_idx + 1
# Do we have any more goals left?
# If we have no more goals left, just stop
if (self.goal_idx > self.goal_max_idx):
self.get_logger().info('Congratulations! All goals have been achieved.')
while True:
pass
# Let's achieve our next goal
else:
# Change the state
self.go_to_goal_state = "adjust heading"
# We need to recalculate the start-goal line if Bug2 is running
self.start_goal_line_calculated = False
else:
pass
def follow_wall(self):
"""
This method causes the robot to follow the boundary of a wall.
"""
# Create a geometry_msgs/Twist message
msg = Twist()
msg.linear.x = 0.0
msg.linear.y = 0.0
msg.linear.z = 0.0
msg.angular.x = 0.0
msg.angular.y = 0.0
msg.angular.z = 0.0
# Special code if Bug2 algorithm is activated
if self.bug2_switch == "ON":
# Calculate the point on the start-goal
# line that is closest to the current position
x_start_goal_line = self.current_x
y_start_goal_line = (
self.start_goal_line_slope_m * (
x_start_goal_line)) + (
self.start_goal_line_y_intercept)
# Calculate the distance between current position
# and the start-goal line
distance_to_start_goal_line = math.sqrt(pow(
x_start_goal_line - self.current_x, 2) + pow(
y_start_goal_line - self.current_y, 2))
# If we hit the start-goal line again
if distance_to_start_goal_line < self.distance_to_start_goal_line_precision:
# Determine if we need to leave the wall and change the mode
# to 'go to goal'
# Let this point be the leave point
self.leave_point_x = self.current_x
self.leave_point_y = self.current_y
# Record the distance to the goal from the leave point
self.distance_to_goal_from_leave_point = math.sqrt(
pow(self.goal_x_coordinates[self.goal_idx]
- self.leave_point_x, 2)
+ pow(self.goal_y_coordinates[self.goal_idx]
- self.leave_point_y, 2))
# Is the leave point closer to the goal than the hit point?
# If yes, go to goal.
diff = self.distance_to_goal_from_hit_point - self.distance_to_goal_from_leave_point
if diff > self.leave_point_to_hit_point_diff:
# Change the mode. Go to goal.
self.robot_mode = "go to goal mode"
# Exit this function
return
# Logic for following the wall
# >d means no wall detected by that laser beam
# <d means an wall was detected by that laser beam
d = self.dist_thresh_wf
if self.leftfront_dist > d and self.front_dist > d and self.rightfront_dist > d:
self.wall_following_state = "search for wall"
msg.linear.x = self.forward_speed
msg.angular.z = -self.turning_speed_wf_slow # turn right to find wall
elif self.leftfront_dist > d and self.front_dist < d and self.rightfront_dist > d:
self.wall_following_state = "turn left"
msg.angular.z = self.turning_speed_wf_fast
elif (self.leftfront_dist > d and self.front_dist > d and self.rightfront_dist < d):
if (self.rightfront_dist < self.dist_too_close_to_wall):
# Getting too close to the wall
self.wall_following_state = "turn left"
msg.linear.x = self.forward_speed
msg.angular.z = self.turning_speed_wf_fast
else:
# Go straight ahead
self.wall_following_state = "follow wall"
msg.linear.x = self.forward_speed
elif self.leftfront_dist < d and self.front_dist > d and self.rightfront_dist > d:
self.wall_following_state = "search for wall"
msg.linear.x = self.forward_speed
msg.angular.z = -self.turning_speed_wf_slow # turn right to find wall
elif self.leftfront_dist > d and self.front_dist < d and self.rightfront_dist < d:
self.wall_following_state = "turn left"
msg.angular.z = self.turning_speed_wf_fast
elif self.leftfront_dist < d and self.front_dist < d and self.rightfront_dist > d:
self.wall_following_state = "turn left"
msg.angular.z = self.turning_speed_wf_fast
elif self.leftfront_dist < d and self.front_dist < d and self.rightfront_dist < d:
self.wall_following_state = "turn left"
msg.angular.z = self.turning_speed_wf_fast
elif self.leftfront_dist < d and self.front_dist > d and self.rightfront_dist < d:
self.wall_following_state = "search for wall"
msg.linear.x = self.forward_speed
msg.angular.z = -self.turning_speed_wf_slow # turn right to find wall
else:
pass
# Send velocity command to the robot
self.publisher_.publish(msg)
def bug2(self):
# Each time we start towards a new goal, we need to calculate the start-goal line
if self.start_goal_line_calculated == False:
# Make sure go to goal mode is set.
self.robot_mode = "go to goal mode"
self.start_goal_line_xstart = self.current_x
self.start_goal_line_xgoal = self.goal_x_coordinates[self.goal_idx]
self.start_goal_line_ystart = self.current_y
self.start_goal_line_ygoal = self.goal_y_coordinates[self.goal_idx]
# Calculate the slope of the start-goal line m
self.start_goal_line_slope_m = (
(self.start_goal_line_ygoal - self.start_goal_line_ystart) / (
self.start_goal_line_xgoal - self.start_goal_line_xstart))
# Solve for the intercept b
self.start_goal_line_y_intercept = self.start_goal_line_ygoal - (
self.start_goal_line_slope_m * self.start_goal_line_xgoal)
# We have successfully calculated the start-goal line
self.start_goal_line_calculated = True
if self.robot_mode == "go to goal mode":
self.go_to_goal()
elif self.robot_mode == "wall following mode":
self.follow_wall()
def main(args=None):
# Initialize rclpy library
rclpy.init(args=args)
# Create the node
controller = PlaceholderController()
# Spin the node so the callback function is called
# Pull messages from any topics this node is subscribed to
# Publish any pending messages to the topics
rclpy.spin(controller)
# Destroy the node explicitly
# (optional - otherwise it will be done automatically
# when the garbage collector destroys the node object)
controller.destroy_node()
# Shutdown the ROS client library for Python
rclpy.shutdown()
if __name__ == '__main__':
main()
Here is the state estimator that goes with the code above. I used an Extended Kalman Filter to filter the odometry measurements from the mobile robot.
# Author: Addison Sears-Collins
# Date: December 8, 2020
# ROS Version: ROS 2 Foxy Fitzroy
# Python math library
import math
# ROS client library for Python
import rclpy
# Used to create nodes
from rclpy.node import Node
# Twist is linear and angular velocity
from geometry_msgs.msg import Twist
# Position, orientation, linear velocity, angular velocity
from nav_msgs.msg import Odometry
# Handles laser distance scan to detect obstacles
from sensor_msgs.msg import LaserScan
# Used for laser scan
from rclpy.qos import qos_profile_sensor_data
# Enable use of std_msgs/Float64MultiArray message
from std_msgs.msg import Float64MultiArray
# Scientific computing library for Python
import numpy as np
class PlaceholderEstimator(Node):
"""
Class constructor to set up the node
"""
def __init__(self):
############## INITIALIZE ROS PUBLISHERS AND SUBSCRIBERS ######
# Initiate the Node class's constructor and give it a name
super().__init__('PlaceholderEstimator')
# Create a subscriber
# This node subscribes to messages of type
# geometry_msgs/Twist.msg
# The maximum number of queued messages is 10.
self.velocity_subscriber = self.create_subscription(
Twist,
'/en613/cmd_vel',
self.velocity_callback,
10)
# Create a subscriber
# This node subscribes to messages of type
# nav_msgs/Odometry
self.odom_subscriber = self.create_subscription(
Odometry,
'/en613/odom',
self.odom_callback,
10)
# Create a publisher
# This node publishes the estimated position (x, y, yaw)
# The type of message is std_msgs/Float64MultiArray
self.publisher_state_est = self.create_publisher(
Float64MultiArray,
'/en613/state_est',
10)
############# STATE TRANSITION MODEL PARAMETERS ###############
# Time step from one time step t-1 to the next time step t
self.delta_t = 0.002 # seconds
# Keep track of the estimate of the yaw angle
# for control input vector calculation.
self.est_yaw = 0.0
# A matrix
# 3x3 matrix -> number of states x number of states matrix
# Expresses how the state of the system [x,y,yaw] changes
# from t-1 to t when no control command is executed. Typically
# a robot on wheels only drives when the wheels are commanded
# to turn.
# For this case, A is the identity matrix.
# A is sometimes F in the literature.
self.A_t_minus_1 = np.array([ [1.0, 0, 0],
[ 0,1.0, 0],
[ 0, 0, 1.0]])
# The estimated state vector at time t-1 in the global
# reference frame
# [x_t_minus_1, y_t_minus_1, yaw_t_minus_1]
# [meters, meters, radians]
self.state_vector_t_minus_1 = np.array([0.0,0.0,0.0])
# The control input vector at time t-1 in the global
# reference frame
# [v,v,yaw_rate]
# [meters/second, meters/second, radians/second]
# In the literature, this is commonly u.
self.control_vector_t_minus_1 = np.array([0.001,0.001,0.001])
# Noise applied to the forward kinematics (calculation
# of the estimated state at time t from the state transition
# model of the mobile robot. This is a vector with the
# number of elements equal to the number of states.
self.process_noise_v_t_minus_1 = np.array([0.096,0.096,0.032])
############# MEASUREMENT MODEL PARAMETERS ####################
# Measurement matrix H_t
# Used to convert the predicted state estimate at time t=1
# into predicted sensor measurements at time t=1.
# In this case, H will be the identity matrix since the
# estimated state maps directly to state measurements from the
# odometry data [x, y, yaw]
# H has the same number of rows as sensor measurements
# and same number of columns as states.
self.H_t = np.array([ [1.0, 0, 0],
[ 0,1.0, 0],
[ 0, 0, 1.0]])
# Sensor noise. This is a vector with the
# number of elements as the number of sensor measurements.
self.sensor_noise_w_t = np.array([0.07,0.07,0.04])
############# EXTENDED KALMAN FILTER PARAMETERS ###############
# State covariance matrix P_t_minus_1
# This matrix has the same number of rows (and columns) as the
# number of states (i.e. 3x3 matrix). P is sometimes referred
# to as Sigma in the literature. It represents an estimate of
# the accuracy of the state estimate at t=1 made using the
# state transition matrix. We start off with guessed values.
self.P_t_minus_1 = np.array([ [0.1, 0, 0],
[ 0,0.1, 0],
[ 0, 0, 0.1]])
# State model noise covariance matrix Q_t
# When Q is large, the Kalman Filter tracks large changes in
# the sensor measurements more closely than for smaller Q.
# Q is a square matrix that has the same number of rows as
# states.
self.Q_t = np.array([ [1.0, 0, 0],
[ 0, 1.0, 0],
[ 0, 0, 1.0]])
# Sensor measurement noise covariance matrix R_t
# Has the same number of rows and columns as sensor measurements.
# If we are sure about the measurements, R will be near zero.
self.R_t = np.array([ [1.0, 0, 0],
[ 0, 1.0, 0],
[ 0, 0, 1.0]])
def velocity_callback(self, msg):
"""
Listen to the velocity commands (linear forward velocity
in the x direction in the robot's reference frame and
angular velocity (yaw rate) around the robot's z-axis.
Convert those velocity commands into a 3-element control
input vector ...
[v,v,yaw_rate]
[meters/second, meters/second, radians/second]
"""
# Forward velocity in the robot's reference frame
v = msg.linear.x
# Angular velocity around the robot's z axis
yaw_rate = msg.angular.z
# [v,v,yaw_rate]
self.control_vector_t_minus_1[0] = v
self.control_vector_t_minus_1[1] = v
self.control_vector_t_minus_1[2] = yaw_rate
def odom_callback(self, msg):
"""
Receive the odometry information containing the position and orientation
of the robot in the global reference frame.
The position is x, y, z.
The orientation is a x,y,z,w quaternion.
"""
roll, pitch, yaw = self.euler_from_quaternion(
msg.pose.pose.orientation.x,
msg.pose.pose.orientation.y,
msg.pose.pose.orientation.z,
msg.pose.pose.orientation.w)
obs_state_vector_x_y_yaw = [msg.pose.pose.position.x,msg.pose.pose.position.y,yaw]
# These are the measurements taken by the odometry in Gazebo
z_t_observation_vector = np.array([obs_state_vector_x_y_yaw[0],
obs_state_vector_x_y_yaw[1],
obs_state_vector_x_y_yaw[2]])
# Apply the Extended Kalman Filter
# This is the updated state estimate after taking the latest
# sensor (odometry) measurements into account.
updated_state_estimate_t = self.ekf(z_t_observation_vector)
# Publish the estimate state
self.publish_estimated_state(updated_state_estimate_t)
def publish_estimated_state(self, state_vector_x_y_yaw):
"""
Publish the estimated pose (position and orientation) of the
robot to the '/en613/state_est' topic.
:param: state_vector_x_y_yaw [x, y, yaw]
x is in meters, y is in meters, yaw is in radians
"""
msg = Float64MultiArray()
msg.data = state_vector_x_y_yaw
self.publisher_state_est.publish(msg)
def euler_from_quaternion(self, x, y, z, w):
"""
Convert a quaternion into euler angles (roll, pitch, yaw)
roll is rotation around x in radians (counterclockwise)
pitch is rotation around y in radians (counterclockwise)
yaw is rotation around z in radians (counterclockwise)
"""
t0 = +2.0 * (w * x + y * z)
t1 = +1.0 - 2.0 * (x * x + y * y)
roll_x = math.atan2(t0, t1)
t2 = +2.0 * (w * y - z * x)
t2 = +1.0 if t2 > +1.0 else t2
t2 = -1.0 if t2 < -1.0 else t2
pitch_y = math.asin(t2)
t3 = +2.0 * (w * z + x * y)
t4 = +1.0 - 2.0 * (y * y + z * z)
yaw_z = math.atan2(t3, t4)
return roll_x, pitch_y, yaw_z # in radians
def getB(self,yaw,dt):
"""
Calculates and returns the B matrix
3x3 matix -> number of states x number of control inputs
The control inputs are the forward speed and the rotation
rate around the z axis from the x-axis in the
counterclockwise direction.
[v,v,yaw_rate]
Expresses how the state of the system [x,y,yaw] changes
from t-1 to t
due to the control commands (i.e. inputs).
:param yaw: The yaw (rotation angle around the z axis) in rad
:param dt: The change in time from time step t-1 to t in sec
"""
B = np.array([ [np.cos(yaw) * dt, 0, 0],
[ 0, np.sin(yaw) * dt, 0],
[ 0, 0, dt]])
return B
def ekf(self,z_t_observation_vector):
"""
Extended Kalman Filter. Fuses noisy sensor measurement to
create an optimal estimate of the state of the robotic system.
INPUT
:param z_t_observation_vector The observation from the Odometry
3x1 NumPy Array [x,y,yaw] in the global reference frame
in [meters,meters,radians].
OUTPUT
:return state_estimate_t optimal state estimate at time t
[x,y,yaw]....3x1 list --->
[meters,meters,radians]
"""
######################### Predict #############################
# Predict the state estimate at time t based on the state
# estimate at time t-1 and the control input applied at time
# t-1.
state_estimate_t = self.A_t_minus_1 @ (
self.state_vector_t_minus_1) + (
self.getB(self.est_yaw,self.delta_t)) @ (
self.control_vector_t_minus_1) + (
self.process_noise_v_t_minus_1)
# Predict the state covariance estimate based on the previous
# covariance and some noise
P_t = self.A_t_minus_1 @ self.P_t_minus_1 @ self.A_t_minus_1.T + (
self.Q_t)
################### Update (Correct) ##########################
# Calculate the difference between the actual sensor measurements
# at time t minus what the measurement model predicted
# the sensor measurements would be for the current timestep t.
measurement_residual_y_t = z_t_observation_vector - (
(self.H_t @ state_estimate_t) + (
self.sensor_noise_w_t))
# Calculate the measurement residual covariance
S_t = self.H_t @ P_t @ self.H_t.T + self.R_t
# Calculate the near-optimal Kalman gain
# We use pseudoinverse since some of the matrices might be
# non-square or singular.
K_t = P_t @ self.H_t.T @ np.linalg.pinv(S_t)
# Calculate an updated state estimate for time t
state_estimate_t = state_estimate_t + (K_t @ measurement_residual_y_t)
# Update the state covariance estimate for time t
P_t = P_t - (K_t @ self.H_t @ P_t)
#### Update global variables for the next iteration of EKF ####
# Update the estimated yaw
self.est_yaw = state_estimate_t[2]
# Update the state vector for t-1
self.state_vector_t_minus_1 = state_estimate_t
# Update the state covariance matrix
self.P_t_minus_1 = P_t
######### Return the updated state estimate ###################
state_estimate_t = state_estimate_t.tolist()
return state_estimate_t
def main(args=None):
"""
Entry point for the progam.
"""
# Initialize rclpy library
rclpy.init(args=args)
# Create the node
estimator = PlaceholderEstimator()
# Spin the node so the callback function is called.
# Pull messages from any topics this node is subscribed to.
# Publish any pending messages to the topics.
rclpy.spin(estimator)
# Destroy the node explicitly
# (optional - otherwise it will be done automatically
# when the garbage collector destroys the node object)
estimator.destroy_node()
# Shutdown the ROS client library for Python
rclpy.shutdown()
if __name__ == '__main__':
main()
Wall Following Robot Mode Demo
Just for fun, I created a switch in the first section of the code (see previous section) that enables you to have the robot do nothing but follow walls. Here is a video demonstration of that.
Obstacle Avoidance Robot Mode Demo
Here is a demo of what the robot looks like when it does nothing but wander around the room, avoiding obstacles and walls.