K-Nearest Neighbors Algorithm From Scratch | Machine Learning

In this post, I will walk you through the k-nearest neighbors algorithm (k-NN classification and k-NN regression), step-by-step. We will develop the code for the algorithm from scratch using Python. We will then run the algorithm on a real-world data set, the image segmentation data set from the UCI Machine Learning Repository. The purpose of the data set is to classify the instances into seven different outdoor images (e.g. sky, foliage, cement, window, path, grass, etc.) based on pixel data. This data set gives a taste of computer vision mixed with machine learning.

Without further ado, let’s get started!

What is the K-Nearest Neighbors Algorithm?
K-Nearest Neighbors Algorithm Design
K-Nearest Neighbors Algorithm in Python, Coded From Scratch
Output Statistics of the K-Nearest Neighbors Algorithm on the Image Segmentation Data Set
Condensed K-Nearest Neighbors Algorithm

What is the K-Nearest Neighbors Algorithm?

The K-Nearest Neighbors Algorithm is a supervised learning algorithm (the target variable we want to predict is available) that is used for both classification and regression problems. Let’s see how it works for both types of problems.

K-Nearest Neighbors Classification

For the k-NN classification algorithm, we have N training instances. Let us suppose that these training instances fall into one of two classes, A and B.

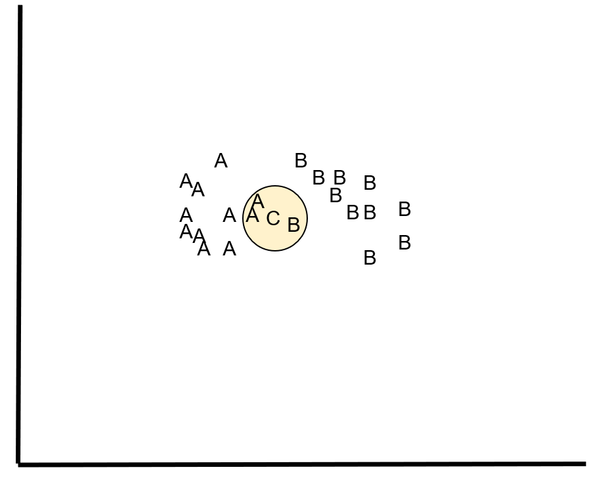
We want to classify a new instance C. We do this by identifying the k nearest neighbors of C and classifying C based on the class that had the most nearest neighbors to C (out of a total of k nearest neighbors).

For example, let k = 3. The three nearest neighbors of C are A, A, and B. Since A had the most nearest neighbors, C belongs to class A.

How do we select k?

A common method for choosing k is to take the square root of N, the number of instances and subtract 1 if that number is odd. However, in this project, we will tune the value for k and record the results to see which value for k achieved optimal performance as measured by either classification accuracy or mean squared error.

How do we determine the k nearest neighbors?

A common method for measuring distance is to use the Euclidean distance formula. That is, given points p =(p₁,p₂,…,p_n) and q = (q₁,q₂,…,q_n), the distance d between p and q is:

d(p,q) = √((q₁– p₁)² + (q₂-p₂)² + …+(q_n– p_n)²)

This is a version of the Pythagorean Theorem.

In short, the algorithm for k-NN classification is as follows. For each test instance, we:

Compute the distance to every training instance
Select the k closest instances and their class
Output the class that occurs most frequently among the k closest instances

Special notes on k-NN classification:

Select an odd value for k for two-class problems in order to avoid ties.
Complexity of the algorithm depends on finding the nearest neighbor for each training instance.
k-NN needs labeled data sets.

k-NN is known as a lazy learning algorithm because a model is not built until the time a test instance arrives. Thus, there is no prior training on the training data as would be the case with an eager learning algorithm.

Also k-NN is a non-parametric algorithm because it does not assume any particular form of the data set (unlike algorithms like linear regression, logistic regression, etc.). The only assumption is that Euclidean distance can be consistently calculated between points.

K-Nearest Neighbors Regression

k-NN regression is a minor modification of k-NN classification. In k-NN regression, we are trying to predict a real number instead of a class. Instead of classifying a test instance based on the most frequently occurring class among the k nearest neighbors, we take the average of the target variable of the k nearest neighbors.

For example, let’s suppose we wanted to predict the age of someone given their weight. We have the following data:

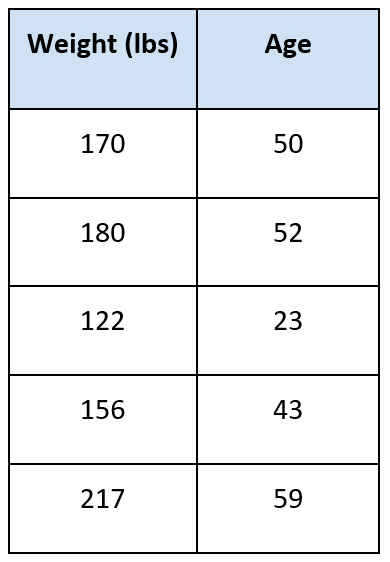
The question is: how old is someone given they weigh 175 pounds?

Suppose k = 3. We find the three nearest neighbors to 175. They are:

(170,50)
(180,52)
(156,43)

We take the average of the target variable:

Average = (50 + 52 + 43) / 3 = 48.3

This is our answer.

In short, the algorithm for k-NN regression is as follows. For each test instance, we:

Compute the distance to every training instance
Select the k closest instances and the values of their target variables
Output the mean of the values of the target variables

Return to Table of Contents

K-Nearest Neighbors Algorithm Design

The first thing we need to do is preprocess the image segmentation data set so that it meets the input requirements of both algorithms. Below is the required data format. I downloaded the data into Microsoft Excel and then made sure I had the following columns:

Columns (0 through N)

0: Instance ID
1: Attribute 1
2: Attribute 2
3: Attribute 3
…
N: Actual Class

Modification of Attribute Values

The image segmentation data set contains 19 attributes, 210 instances, and 7 classes. This data set was created from a database of seven outdoor images. Below are some of the modifications I made.

Classes were made numerical:

BRICKFACE = 1.0
SKY = 2.0
FOLIAGE = 3.0
CEMENT = 4.0
WINDOW = 5.0
PATH = 6.0
GRASS = 7.0

Region-pixel-count was removed since it was 9 for all instances.

I also normalized the attributes so that they are all between 0 and 1.

Here is what the first few columns of your data set should look like after all that preprocessing:

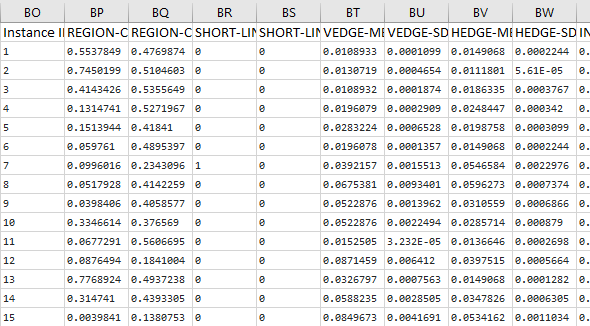
Save the file as a csv file (comma-delimited), and load it into the program below (Python).

Here is a link to the final data set I used.

Return to Table of Contents

K-Nearest Neighbors Algorithm in Python, Coded From Scratch

Here is the full code for the k-nearest neighbors algorithm (Note that I used five-fold stratified cross-validation to produce the final classification accuracy statistics). You might want to copy and paste it into a document since it is pretty large and hard to see on a single web page. Don’t be scared at how long this code is. I include a lot of comments so that you know what is going on at each step:

import numpy as np # Import Numpy library

# File name: knn.py
# Author: Addison Sears-Collins
# Date created: 6/20/2019
# Python version: 3.7
# Description: Implementation of the k-nearest neighbors algorithm (k-NN)
# from scratch

# Required Data Set Format for Classification Problems:
# Must be all numerical
# Columns (0 through N)
# 0: Instance ID
# 1: Attribute 1 
# 2: Attribute 2
# 3: Attribute 3 
# ...
# N: Actual Class

# Required Data Set Format for Regression Problems:
# Must be all numerical
# Columns (0 through N)
# 0: Instance ID
# 1: Attribute 1 
# 2: Attribute 2
# 3: Attribute 3 
# ...
# N: Actual Class
# N + 1: Stratification Bin

class Knn:

    # Constructor
    #   Parameters:
    #     k: k value for k-NN
    #     problem_type: ('r' for regression or 'c' for classification)
    def __init__(self, k, problem_type):
        self.__k = k
        self.__problem_type = problem_type

    # Parameters:
    #   training_set: The folds used for training (2d numpy array)
    #   test_instance: The test instance we need to find the neighbors for 
    #                  (numpy array)
    # Returns: 
    #   The k most similar neighbors from the training set for a given 
    #   test instance. It will be a 2D numpy array where the first column 
    #   will hold the Actual class value of the training instance and the 
    #   second column will store the distance to the test instance...
    #   (actual class value, distance). 
    def get_neighbors(self, training_set, test_instance):

        # Record the number of training instances in the training set
        no_of_training_instances = np.size(training_set,0)

        # Record the number of columns in the training set
        no_of_training_columns = np.size(training_set,1)

        # Record the column index of the actual class of the training_set
        actual_class_column = None
        # If classification problem
        if self.__problem_type == "c":
            actual_class_column = no_of_training_columns - 1
        # If regression problem
        else:
            actual_class_column = no_of_training_columns - 2

        # Create an empty 2D array called actual_class_and_distance. This 
        # array should be the same length as the number of training instances. 
        # The first column will hold the Actual Class value of the training 
        # instance, and the second column will store the distance to the 
        # test instance...(actual class value, distance). 
        actual_class_and_distance = np.zeros((no_of_training_instances, 2))

        neighbors = None

        # For each row (training instance) in the training set
        for row in range(0, no_of_training_instances):

            # Record the actual class value in the 
            # actual_class_and_distance array (column 0)
            actual_class_and_distance[row,0] = training_set[
                row,actual_class_column]

            # Initialize a temporary training instance copied from this 
            # training instance
            temp_training_instance = np.copy(training_set[row,:])

            # Initialize a temporary test instance copied from this 
            # test_instance
            temp_test_instance = np.copy(test_instance)

            # If this is a classification problem
            if self.__problem_type == "c":
            
                # Update temporary training instance with Instance ID 
                # and the Actual Class pieces removed
                temp_training_instance = np.delete(temp_training_instance,[
                    0,actual_class_column])

                # Update temporary test instance with the Instance ID 
                # and the Actual Class pieces removed
                temp_test_instance = np.delete(temp_test_instance,[
                    0,actual_class_column])

            # If this is a regression problem
            else:

                # Update temporary training instance with Instance ID, Actual 
                # Class, and Stratification Bin pieces removed
                temp_training_instance = np.delete(temp_training_instance,[
                    0,actual_class_column,actual_class_column+1])

                # Update temporary test instance with the Instance ID, Actual
                # Class, and Stratification Bin pieces removed
                temp_test_instance = np.delete(temp_test_instance,[
                    0,actual_class_column,actual_class_column+1])

            # Calculate the euclidean distance from the temporary test
            # instance to the temporary training instance
            distance = np.linalg.norm(
                temp_test_instance - temp_training_instance)

            # Record the distance in the actual_class_and_distance 
            # array (column 1)
            actual_class_and_distance[row,1] = distance

        # Sort the actual_class_and_distance 2D array by the 
        # distance column (column 1) in ascending order.
        actual_class_and_distance = actual_class_and_distance[
                actual_class_and_distance[:,1].argsort()]

        k = self.__k

        # Extract the first k rows of the actual_class_and_distance array
        neighbors = actual_class_and_distance[:k,:]

        return neighbors

    # Generate a prediction based on the most frequent class or averaged 
    # target variable value of the neighbors
    # Parameters: 
    #   neighbors - 1D array (actual_class_value)
    # Returns:
    #   predicted_class_value
    def make_prediction(self, neighbors):
    
        prediction = None

        # If this is a classification problem
        if self.__problem_type == "c":
            
            #  Prediction is the most frequent value in column 0 of
            #  the neighbors array
            neighborsint = neighbors.astype(int)
            prediction = np.bincount(neighborsint).argmax()
            
        # If this is a regression problem
        else:

            # Prediction is the average of the neighbors array
            prediction = np.mean(neighbors)

        return prediction

    # Parameters: 
    #   actual_class_array
    #   predicted_class_array
    # Returns: 
    #   accuracy: Either classification accuracy (for 
    #   classification problems) or 
    #   mean squared error (for regression problems)
    def get_accuracy(self, actual_class_array, predicted_class_array):

        # Initialize accuracy variable
        accuracy = None

        # Initialize decision variable
        decision = None

        counter = None

        actual_class_array_size = actual_class_array.size

        # If this is a classification problem
        if self.__problem_type == "c":
            
            counter = 0

            # For each element in the actual class array
            for row in range(0,actual_class_array_size):

                # If actual class value is equal to value in predicted
                # class array
                if actual_class_array[row] == predicted_class_array[row]:
                    decision = "correct"
                    counter += 1
                else:
                    decision = "incorrect"

            classification_accuracy = counter / (actual_class_array_size)

            accuracy = classification_accuracy

        # If this is a regression problem
        else:

            # Initialize an empty squared error array. 
            # Needs to be same length as number of test instances
            squared_error_array = np.empty(actual_class_array_size)

            squared_error = None

            # For each element in the actual class array
            for row in range(0,actual_class_array_size):

                # Calculate the squared error
                squared_error = (abs((actual_class_array[
                        row] - predicted_class_array[row]))) 
                squared_error *= squared_error
                squared_error_array[row] = squared_error

            mean_squared_error = np.mean(squared_error_array)
            
            accuracy = mean_squared_error
        
        return accuracy

Here is the driver program that calls and executes the code above:

import pandas as pd # Import Pandas library 
import numpy as np # Import Numpy library
from five_fold_stratified_cv import FiveFoldStratCv
from knn import Knn

# File name: knn_driver.py
# Author: Addison Sears-Collins
# Date created: 6/20/2019
# Python version: 3.7
# Description: Driver for the knn.py program 
# (K-Nearest Neighbors)

# Required Data Set Format for Classification Problems:
# Must be all numerical
# Columns (0 through N)
# 0: Instance ID
# 1: Attribute 1 
# 2: Attribute 2
# 3: Attribute 3 
# ...
# N: Actual Class

# Required Data Set Format for Regression Problems:
# Must be all numerical
# Columns (0 through N)
# 0: Instance ID
# 1: Attribute 1 
# 2: Attribute 2
# 3: Attribute 3 
# ...
# N: Actual Class
# N + 1: Stratification Bin

################# INPUT YOUR OWN VALUES IN THIS SECTION ######################
ALGORITHM_NAME = "K-Nearest Neighbor"
SEPARATOR = ","  # Separator for the data set (e.g. "\t" for tab data)
##############################################################################

def main():

    print("Welcome to the " +  ALGORITHM_NAME + " program!")
    print()
    print("Running " + ALGORITHM_NAME + ". Please wait...")
    print()

    # k value that will be tuned
    k = eval(input("Enter a value for k: ") )

    # "c" for classification or "r" for regression
    problem = input("Press  \"c\" for classification or \"r\" for regression: ") 

    # Directory where data set is located
    data_path = input("Enter the path to your input file: ") 

    # Read the full text file and store records in a Pandas dataframe
    pd_data_set = pd.read_csv(data_path, sep=SEPARATOR)

    # Convert dataframe into a Numpy array
    np_data_set = pd_data_set.to_numpy(copy=True)

    # Show functioning of the program
    trace_runs_file = input("Enter the name of your trace runs file: ") 

    # Open a new file to save trace runs
    outfile_tr = open(trace_runs_file,"w") 

    # Testing statistics
    test_stats_file = input("Enter the name of your test statistics file: ") 

    # Open a test_stats_file 
    outfile_ts = open(test_stats_file,"w")

    # Create an object of class FiveFoldStratCv
    fivefolds1 = FiveFoldStratCv(np_data_set,problem)

    # The number of folds in the cross-validation
    NO_OF_FOLDS = 5 

    # Create an object of class Knn
    knn1 = Knn(k,problem) 

    # Generate the five stratified folds
    fold0, fold1, fold2, fold3, fold4 = fivefolds1.get_five_folds()

    training_dataset = None
    test_dataset = None

    # Create an empty array of length 5 to store the accuracy_statistics 
    # (classification accuracy for classification problems or mean squared
    # error for regression problems)
    accuracy_statistics = np.zeros(NO_OF_FOLDS)

    # Run k-NN the designated number of times as indicated by the number of folds
    for experiment in range(0, NO_OF_FOLDS):

        print()
        print("Running Experiment " + str(experiment + 1) + " ...")
        print()
        outfile_tr.write("Running Experiment " + str(experiment + 1) + " ...\n")
        outfile_tr.write("\n")

        # Each fold will have a chance to be the test data set
        if experiment == 0:
            test_dataset = fold0
            training_dataset = np.concatenate((
                fold1, fold2, fold3, fold4), axis=0)
        elif experiment == 1:
            test_dataset = fold1
            training_dataset = np.concatenate((
                fold0, fold2, fold3, fold4), axis=0)
        elif experiment == 2:
            test_dataset = fold2
            training_dataset = np.concatenate((
                fold0, fold1, fold3, fold4), axis=0)
        elif experiment == 3:
            test_dataset = fold3
            training_dataset = np.concatenate((
                fold0, fold1, fold2, fold4), axis=0)
        else:
            test_dataset = fold4
            training_dataset = np.concatenate((
                fold0, fold1, fold2, fold3), axis=0)

        # Actual class column index of the test dataset
        actual_class_column = None           
     
        # If classification problem
        if problem == "c":
            actual_class_column = np.size(test_dataset,1) - 1
        # If regression problem
        else:
            actual_class_column = np.size(test_dataset,1) - 2

        # Create an array of the actual_class_values of the test instances
        actual_class_values = test_dataset[:,actual_class_column]

        no_of_test_instances = np.size(test_dataset,0)

        # Make an empty array called predicted_class_values which will 
        # store the predicted class values. It should be the same length 
        # as the number of test instances
        predicted_class_values = np.zeros(no_of_test_instances)

        # For each row in the test data set
        for row in range(0, no_of_test_instances):
  
            # Neighbor array is a 2D array containing the neighbors 
            # (actual class value, distance) 
            # Get the k nearest neighbors for each test instance
            this_instance = test_dataset[row,:]
            neighbor_array = knn1.get_neighbors(training_dataset,this_instance)

            # Extract the actual class values
            neighbors_arr = neighbor_array[:,0]
  
            # Predicted class value stored in the variable prediction
            prediction = knn1.make_prediction(neighbors_arr)
  
            # Record the prediction in the predicted_class_values array
            predicted_class_values[row] = prediction

        # Calculate the classification accuracy of the predictions 
        # (k-NN classification) or the mean squared error (k-NN regression)
        accuracy = knn1.get_accuracy(actual_class_values,predicted_class_values)

        # Store the accuracy in the accuracy_statistics array
        accuracy_statistics[experiment] = accuracy

        # If classification problem
        if problem == "c":
            temp_acc = accuracy * 100
            outfile_tr.write("Classification Accuracy: " + str(temp_acc) + "%\n")
            outfile_tr.write("\n")
            print("Classification Accuracy: " + str(temp_acc) + "%\n")
        # If regression problem
        else:
            outfile_tr.write("Mean Squared Error: " + str(accuracy) + "\n")
            outfile_tr.write("\n")
            print("Mean Squared Error: " + str(accuracy) + "\n")

    outfile_tr.write("Experiments Completed.\n")
    print("Experiments Completed.")
    print()

    # Write to a file
    outfile_ts.write("----------------------------------------------------------\n")
    outfile_ts.write(ALGORITHM_NAME + " Summary Statistics\n")
    outfile_ts.write("----------------------------------------------------------\n")
    outfile_ts.write("Data Set : " + data_path + "\n")
    outfile_ts.write("\n")
    outfile_ts.write("Accuracy Statistics for All 5 Experiments:")
    outfile_ts.write(np.array2string(
        accuracy_statistics, precision=2, separator=',',
        suppress_small=True))
    outfile_ts.write("\n")

    # Write the relevant stats to a file
    outfile_ts.write("\n")

    if problem == "c":
        outfile_ts.write("Problem Type : Classification" + "\n")
    else:
        outfile_ts.write("Problem Type : Regression" + "\n")

    outfile_ts.write("\n")
    outfile_ts.write("Value for k : " + str(k) + "\n")
    outfile_ts.write("\n")

    accuracy = np.mean(accuracy_statistics)

    if problem == "c":
        accuracy *= 100
        outfile_ts.write("Classification Accuracy : " + str(accuracy) + "%\n")
    else: 
        outfile_ts.write("Mean Squared Error : " + str(accuracy) + "\n")

    # Print to the console
    print()
    print("----------------------------------------------------------")
    print(ALGORITHM_NAME + " Summary Statistics")
    print("----------------------------------------------------------")
    print("Data Set : " + data_path)
    print()
    print()
    print("Accuracy Statistics for All 5 Experiments:")
    print(accuracy_statistics)
    print()
    # Write the relevant stats to a file
    print()

    if problem == "c":
        print("Problem Type : Classification")
    else:
        print("Problem Type : Regression")

    print()
    print("Value for k : " + str(k))
    print()
    if problem == "c":
        print("Classification Accuracy : " + str(accuracy) + "%")
    else: 
        print("Mean Squared Error : " + str(accuracy))

    print()

    # Close the files
    outfile_tr.close()
    outfile_ts.close()

main()

Return to Table of Contents

Output Statistics of the K-Nearest Neighbors Algorithm on the Image Segmentation Data Set

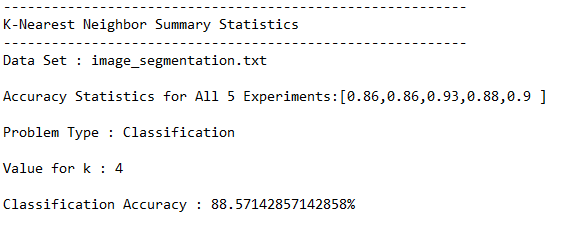
This section shows the results for the runs of the k-nearest neighbors algorithm on the image segmentation data set. I used a k-value of 4, but you can feel free to change this and see what accuracy value you get.

Test Statistics

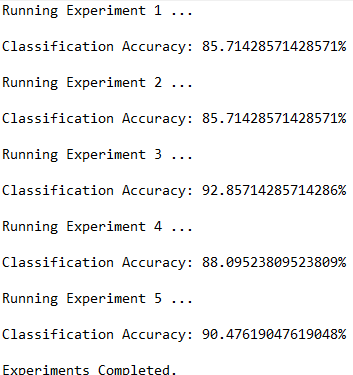
Trace Runs

Here are the trace runs of the algorithm:

Return to Table of Contents

Condensed K-Nearest Neighbors Algorithm

The time and space complexity of the regular k-nearest neighbors algorithm described above is directly proportional to the number of instances in the training set. This could potentially present a problem with massively large data sets. This is where the condensed k-nearest neighbors algorithm (ck-NN) comes in handy.

The idea behind ck-NN is to reduce the size of the training set by selecting the smallest subset of the training data set that results in no loss of classification accuracy. By systematically removing ineffective instances, we reduce the computation time as well as the storage requirement.

Here is how condensed k-NN works:

We start with an empty bin called STORE.

1. Place the first instance in STORE

2. Check whether the second instance can be classified correctly by 1-nearest neighbor using the instance in STORE as the reference.

3. Repeat step 2 for all other instances in the data set.

4. Repeat step 2 on the data set, doing continuous passes over the data set until either

5. Use the instances in STORE as the input for the k-NN classification algorithm.

Here is the code in Python for ck-NN:

import numpy as np # Import Numpy library
from knn import Knn

# File name: cknn.py
# Author: Addison Sears-Collins
# Date created: 6/21/2019
# Python version: 3.7
# Description: Implementation of the condensed k-nearest neighbors 
# algorithm (k-NN) from scratch

# Required Data Set Format for Classification Problems:
# Must be all numerical
# Columns (0 through N)
# 0: Instance ID
# 1: Attribute 1 
# 2: Attribute 2
# 3: Attribute 3 
# ...
# N: Actual Class

class CondensedKnn:

    # Constructor
    #   Parameters:
    #     training_set: The training set that we need to prune
    #     problem_type: ('c' for classification)
    def __init__(self, training_set, problem_type="c"):
        self.__training_set = training_set
        self.__problem_type = problem_type

    # Parameters:
    #   None.
    # Returns: 
    #   A training set that has irrelevant instances removed 
    def get_trainingset(self):
        
        # Initialize a condensed training set. Copy it from the actual 
        # training set
        condensed_training_set = np.copy(self.__training_set)

        # Record the number of instances in the condensed training_set
        no_of_training_instances = np.size(condensed_training_set,0)

        # Record the number of columns in the condensed training set
        no_of_training_columns = np.size(condensed_training_set,1)

        # Print the initial number of instances in the condensed training set
        print("\nBefore condensing: " + str(
            no_of_training_instances) + " training instances\n")

        # Record the column index of the actual class of the training_set
        actual_class_column = no_of_training_columns - 1

        # Initialize an array named store with the first instance of the 
        # condensed training_set
        store = np.copy(condensed_training_set[0,:])

        # Create a 2D array
        new_row = np.copy(condensed_training_set[0,:])
        store = np.vstack([store,new_row])

        # For the second instance to the last instance in the condensed 
        # training_set
        row = 1
        while row < no_of_training_instances:
            
            # Record the actual class value
            actual_class_value = condensed_training_set[
                row,actual_class_column]

            # Create an object of class Knn
            knn1 = Knn(1,self.__problem_type) 

            # Neighbor array is a 2D array containing the neighbors 
            # (actual class value, distance) 
            # Get the nearest neighbor for each instance
            this_instance = condensed_training_set[row,:]
            neighbor_array = knn1.get_neighbors(store,this_instance)

            # Extract the actual class values
            neighbors_arr = neighbor_array[:,0]
  
            # Predicted class value stored in the variable prediction
            prediction = knn1.make_prediction(neighbors_arr)

            # If actual class value is not equal to the prediction
            # Append that instance to the store array
            # Remove this instance from the condensed training_set
            if actual_class_value != prediction:
                new_row = np.copy(this_instance)
                store = np.vstack([store,new_row])

                condensed_training_set = np.delete(
                    condensed_training_set, row, 0)
                no_of_training_instances -= 1
            
            row += 1

        # Declare the stopping criteria. We stop when either one complete
        # pass is made through the condensed training set with no more 
        # transfers of instances to store or there are no more instances 
        # remaining in the condensed training data set
  
        no_more_transfers_to_store = False
        no_more_instances_left = None
  
        # Update the number of instances in the condensed training_set
        no_of_training_instances = np.size(condensed_training_set,0)
        
        if no_of_training_instances > 0:
            no_more_instances_left = False
        else:
            no_more_instances_left = True

        while not(no_more_transfers_to_store) and not(no_more_instances_left):
            # Reset the number of transfers_made to 0
            transfers_made = 0

            # For the second instance to the last instance in the condensed 
            # training_set
            row = 0
            while row < no_of_training_instances:

                # Record the actual class value
                actual_class_value = condensed_training_set[
                    row,actual_class_column]

                # Create an object of class Knn
                knn1 = Knn(1,self.__problem_type) 

                # Neighbor array is a 2D array containing the neighbors 
                # (actual class value, distance) 
                # Get the nearest neighbor for each instance
                this_instance = condensed_training_set[row,:]
                neighbor_array = knn1.get_neighbors(store,this_instance)

                # Extract the actual class values
                neighbors_arr = neighbor_array[:,0]
  
                # Predicted class value stored in the variable prediction
                prediction = knn1.make_prediction(neighbors_arr)

                # If actual class value is not equal to the prediction
                # Append that instance to the store array
                # Remove this instance from the condensed training_set
                if actual_class_value != prediction:
                    new_row = np.copy(this_instance)
                    store = np.vstack([store,new_row])

                    condensed_training_set = np.delete(
                        condensed_training_set, row, 0)
                    no_of_training_instances -= 1
                    transfers_made += 1
            
                row += 1
        
            # Update the number of instances in the condensed training_set
            no_of_training_instances = np.size(condensed_training_set,0)

            if no_of_training_instances > 0:
                no_more_instances_left = False
            else:
                no_more_instances_left = True

            if transfers_made > 0:
                no_more_transfers_to_store = False
            else: 
                no_more_transfers_to_store = True

        # Delete row 0 from the store
        store = np.delete(store,0,0)

        # Print the final number of instances in the store
        print("After condensing: " + str(
            np.size(store,0)) + " training instances\n")
        return store

Here is the code (Python) for the driver that executes the program above. It uses the regular k-NN code I presented earlier in this post as well as the five-fold stratified cross-validation code:

import pandas as pd # Import Pandas library 
import numpy as np # Import Numpy library
from five_fold_stratified_cv import FiveFoldStratCv
from knn import Knn
from cknn import CondensedKnn

# File name: cknn_driver.py
# Author: Addison Sears-Collins
# Date created: 6/21/2019
# Python version: 3.7
# Description: Driver for the cknn.py program 
# (Condensed K-Nearest Neighbors)

# Required Data Set Format for Classification Problems:
# Must be all numerical
# Columns (0 through N)
# 0: Instance ID
# 1: Attribute 1 
# 2: Attribute 2
# 3: Attribute 3 
# ...
# N: Actual Class

################# INPUT YOUR OWN VALUES IN THIS SECTION ######################
ALGORITHM_NAME = "Condensed K-Nearest Neighbor"
SEPARATOR = ","  # Separator for the data set (e.g. "\t" for tab data)
##############################################################################

def main():

    print("Welcome to the " +  ALGORITHM_NAME + " program!")
    print()
    print("Running " + ALGORITHM_NAME + ". Please wait...")
    print()

    # k value that will be tuned
    k = eval(input("Enter a value for k: ") )

    # "c" for classification
    problem = input("Press  \"c\" for classification: ") 

    # Directory where data set is located
    data_path = input("Enter the path to your input file: ") 

    # Read the full text file and store records in a Pandas dataframe
    pd_data_set = pd.read_csv(data_path, sep=SEPARATOR)

    # Convert dataframe into a Numpy array
    np_data_set = pd_data_set.to_numpy(copy=True)

    # Show functioning of the program
    trace_runs_file = input("Enter the name of your trace runs file: ") 

    # Open a new file to save trace runs
    outfile_tr = open(trace_runs_file,"w") 

    # Testing statistics
    test_stats_file = input("Enter the name of your test statistics file: ") 

    # Open a test_stats_file 
    outfile_ts = open(test_stats_file,"w")

    # Create an object of class FiveFoldStratCv
    fivefolds1 = FiveFoldStratCv(np_data_set,problem)

    # The number of folds in the cross-validation
    NO_OF_FOLDS = 5 

    # Create an object of class Knn
    knn1 = Knn(k,problem) 

    # Generate the five stratified folds
    fold0, fold1, fold2, fold3, fold4 = fivefolds1.get_five_folds()

    training_dataset = None
    test_dataset = None

    # Create an empty array of length 5 to store the accuracy_statistics 
    # (classification accuracy for classification problems or mean squared
    # error for regression problems)
    accuracy_statistics = np.zeros(NO_OF_FOLDS)

    # Run k-NN the designated number of times as indicated by the number of folds
    for experiment in range(0, NO_OF_FOLDS):

        print()
        print("Running Experiment " + str(experiment + 1) + " ...")
        print()
        outfile_tr.write("Running Experiment " + str(experiment + 1) + " ...\n")
        outfile_tr.write("\n")

        # Each fold will have a chance to be the test data set
        if experiment == 0:
            test_dataset = fold0
            training_dataset = np.concatenate((
                fold1, fold2, fold3, fold4), axis=0)
        elif experiment == 1:
            test_dataset = fold1
            training_dataset = np.concatenate((
                fold0, fold2, fold3, fold4), axis=0)
        elif experiment == 2:
            test_dataset = fold2
            training_dataset = np.concatenate((
                fold0, fold1, fold3, fold4), axis=0)
        elif experiment == 3:
            test_dataset = fold3
            training_dataset = np.concatenate((
                fold0, fold1, fold2, fold4), axis=0)
        else:
            test_dataset = fold4
            training_dataset = np.concatenate((
                fold0, fold1, fold2, fold3), axis=0)
        
        # Create an object of class CondensedKnn
        cknn1 = CondensedKnn(training_dataset,problem)

        # Get a new, smaller training set with fewer instances
        training_dataset = cknn1.get_trainingset()

        # Actual class column index of the test dataset
        actual_class_column = np.size(test_dataset,1) - 1

        # Create an array of the actual_class_values of the test instances
        actual_class_values = test_dataset[:,actual_class_column]

        no_of_test_instances = np.size(test_dataset,0)

        # Make an empty array called predicted_class_values which will 
        # store the predicted class values. It should be the same length 
        # as the number of test instances
        predicted_class_values = np.zeros(no_of_test_instances)

        # For each row in the test data set
        for row in range(0, no_of_test_instances):
  
            # Neighbor array is a 2D array containing the neighbors 
            # (actual class value, distance) 
            # Get the k nearest neighbors for each test instance
            this_instance = test_dataset[row,:]
            neighbor_array = knn1.get_neighbors(training_dataset,this_instance)

            # Extract the actual class values
            neighbors_arr = neighbor_array[:,0]
  
            # Predicted class value stored in the variable prediction
            prediction = knn1.make_prediction(neighbors_arr)
  
            # Record the prediction in the predicted_class_values array
            predicted_class_values[row] = prediction

        # Calculate the classification accuracy of the predictions 
        # (k-NN classification) or the mean squared error (k-NN regression)
        accuracy = knn1.get_accuracy(actual_class_values,predicted_class_values)

        # Store the accuracy in the accuracy_statistics array
        accuracy_statistics[experiment] = accuracy

        # Stats
        temp_acc = accuracy * 100
        outfile_tr.write("Classification Accuracy: " + str(temp_acc) + "%\n")
        outfile_tr.write("\n")
        print("Classification Accuracy: " + str(temp_acc) + "%\n")


    outfile_tr.write("Experiments Completed.\n")
    print("Experiments Completed.")
    print()

    # Write to a file
    outfile_ts.write("----------------------------------------------------------\n")
    outfile_ts.write(ALGORITHM_NAME + " Summary Statistics\n")
    outfile_ts.write("----------------------------------------------------------\n")
    outfile_ts.write("Data Set : " + data_path + "\n")
    outfile_ts.write("\n")
    outfile_ts.write("Accuracy Statistics for All 5 Experiments:")
    outfile_ts.write(np.array2string(
        accuracy_statistics, precision=2, separator=',',
        suppress_small=True))
    outfile_ts.write("\n")

    # Write the relevant stats to a file
    outfile_ts.write("\n")

    outfile_ts.write("Problem Type : Classification" + "\n")

    outfile_ts.write("\n")
    outfile_ts.write("Value for k : " + str(k) + "\n")
    outfile_ts.write("\n")

    accuracy = np.mean(accuracy_statistics)

    accuracy *= 100
    outfile_ts.write("Classification Accuracy : " + str(accuracy) + "%\n")
   
    # Print to the console
    print()
    print("----------------------------------------------------------")
    print(ALGORITHM_NAME + " Summary Statistics")
    print("----------------------------------------------------------")
    print("Data Set : " + data_path)
    print()
    print()
    print("Accuracy Statistics for All 5 Experiments:")
    print(accuracy_statistics)
    print()
    # Write the relevant stats to a file
    print()

    print("Problem Type : Classification")
    print()
    print("Value for k : " + str(k))
    print()
    print("Classification Accuracy : " + str(accuracy) + "%")
    print()

    # Close the files
    outfile_tr.close()
    outfile_ts.close()

main()

Here are the results for those runs as well as a comparison to regular k-NN:

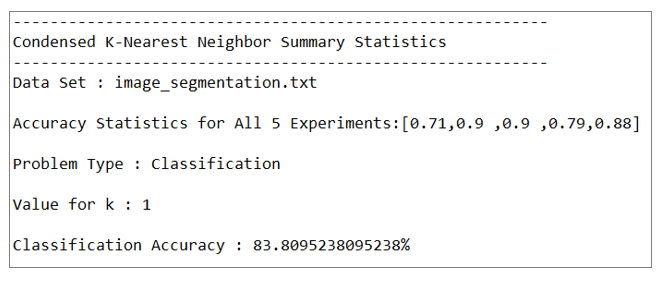
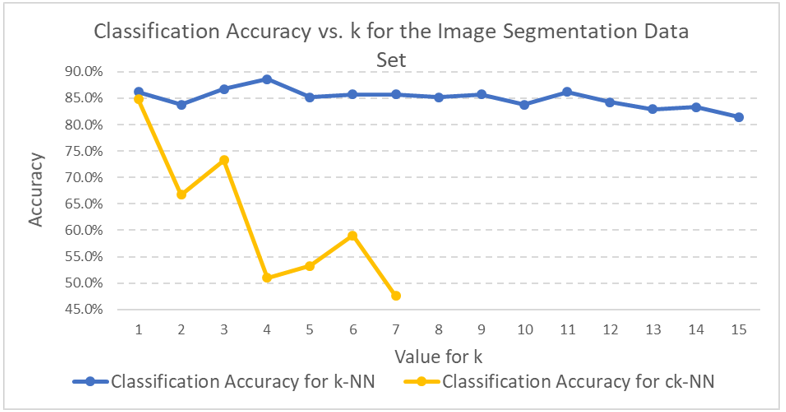
Classification accuracy was greater than 80% for both the k-NN and ck-NN runs. The classification accuracy for the k-NN runs was about 4 percentage points greater than ck-NN. However, the variability of the classification accuracy for the five experiments in the ck-NN runs was greater than for the k-NN runs.

In a real-world setting for classification, I would select the k-NN algorithm over ck-NN because its performance is more consistent. In addition, while ck-NN might result in improved run times for the actual k-NN runs, there is still the prior overhead associated with having to prune the training set of irrelevant instances.

Return to Table of Contents

K-means Clustering Algorithm From Scratch | Machine Learning

In this post, I will walk you through the k-means clustering algorithm, step-by-step. We will develop the code for the algorithm from scratch using Python. We will then run the algorithm on a real-world data set, the iris data set (flower classification) from the UCI Machine Learning Repository. Without further ado, let’s get started!

What is the K-means Clustering Algorithm?
K-means Clustering Algorithm Design
K-means Clustering Algorithm in Python, Coded From Scratch
Output Statistics of K-means Clustering on the Iris Data Set

What is the K-means Clustering Algorithm?

The K-means algorithm is an unsupervised clustering algorithm (the target variable we want to predict is not available) that is used to group unlabeled data set instances into clusters based on similar attributes.

Step 1: Choose a Value for K and Select the Initial Centroids

The first step of K-means is to determine the valve for k, the number of clusters you want to group your data set into. We then randomly select k cluster centroids (i.e. k random instances) from the data set, where k is some positive integer.

Step 2: Cluster Assignment

The next step is the cluster assignment step. This step involves going through each of the instances and assigning that instance to the cluster centroid closest to it.

Step 3: Move Centroid

The next part is the move centroid step. We move each of the k centroids to the average of all the instances that were assigned to that cluster centroid.

Step 4: Repeat Steps 2 and 3 Until Centroids Stop Changing

We keep running the cluster assignment and move centroid steps until the cluster centroids stop changing. At that point, the data is deemed clustered.

Andrew Ng, a professor of machine learning at Stanford University, does a good job of showing you visually how k-means clustering works:

Return to Table of Contents

K-means Clustering Algorithm Design

The first thing we need to do is preprocess the iris data set so that it meets the input requirements of both algorithms. Below is the required data format. I downloaded the data into Microsoft Excel and then made sure I had the following columns:

Columns (0 through N)

0: Instance ID
1: Attribute 1
2: Attribute 2
3: Attribute 3
…
N: Actual Class (used for classification accuracy calculation)

The program then adds 4 additional columns.

N + 1: Cluster
N + 2: Silhouette Coefficient
N + 3: Predicted Class
N + 4: Prediction Correct? (1 if yes, 0 if no)

Here is what your data set should look like:

The iris data set contains 3 classes of 50 instances each (150 instances in total), where each class refers to a different type of iris flower. There are 4 attributes in the data set.

Binarization is optional, but I prefer to do it since it speeds up the attribute selection process. You need to go through each attribute, one by one. Attribute values greater than the mean of the attribute need to be changed to 1, otherwise set it to 0. Here is the general Excel formula:

=IF(B2>AVERAGE(B$2:B$151),1,0)

Here is how the data looks after the binarization:

Save the file as a csv file (comma-delimited), and load it into the program below (Python).

Here is a link to the final data set I used.

Return to Table of Contents

K-means Clustering Algorithm in Python, Coded From Scratch

K-means appears to be particularly sensitive to the starting centroids. The starting centroids for the k clusters were chosen at random. When these centroids started out poor, the algorithm took longer to converge to a solution. Future work would be to fine-tune the initial centroid selection process.

Here is the full code for k-means clustering. Don’t be scared at how long this code is. I include a bunch of comments at each step so that you know what is going on. Just copy and paste this into your favorite IDE and run it!

import pandas as pd # Import Pandas library 
import numpy as np # Import Numpy library

# File name: kmeans.py
# Author: Addison Sears-Collins
# Date created: 6/12/2019
# Python version: 3.7
# Description: Implementation of K-means clustering algorithm from scratch.
# K-means algorithm is a clustering algorithm that is used to group 
# unlabeled data set instances into clusters based on similar attributes.

# Required Data Set Format:
# Columns (0 through N)
# 0: Instance ID
# 1: Attribute 1 
# 2: Attribute 2
# 3: Attribute 3 
# ...
# N: Actual Class (used for classification accuracy calculation)

# This program then adds 4 additional columns.
# N + 1: Cluster
# N + 2: Silhouette Coefficient
# N + 3: Predicted Class
# N + 4: Prediction Correct? (1 if yes, 0 if no)

################ INPUT YOUR OWN VALUES IN THIS SECTION ######################
ALGORITHM_NAME = "K-means"
DATA_PATH = "iris_dataset.txt"  # Directory where data set is located
TEST_STATS_FILE = "iris_dataset_kmeans_test_stats.txt"#Testing statistics
TEST_OUT_FILE = "iris_dataset_kmeans_test_out.txt" # Testing output
# Show functioning of the program
TRACE_RUNS_FILE  = "iris_dataset_kmeans_trace_runs.txt" 
SEPARATOR = ","  # Separator for the data set (e.g. "\t" for tab data)
#############################################################################

# Open a new file to save trace runs
outfile3 = open(TRACE_RUNS_FILE,"w") 

# Read the full text file and store records in a Pandas dataframe
pd_full_data_set = pd.read_csv(DATA_PATH, sep=SEPARATOR)

# Copy the dataframe into a new dataframe so we don't mess up the
# original data
pd_data_set = pd_full_data_set.copy() 

# Calculate the number of instances, columns, and attributes in the
# training data set. Assumes 1 column for the instance ID and 1 column
# for the class. Record the index of the column that contains 
# the actual class
no_of_instances = len(pd_data_set.index) # number of rows
no_of_columns = len(pd_data_set.columns) # number of columns
no_of_attributes = no_of_columns - 2
actual_class_column = no_of_columns - 1

# Store class values in a column and then create a list of unique
# classes and store in a dataframe and a Numpy array
unique_class_list_df = pd_data_set.iloc[:,actual_class_column]
unique_class_list_np = unique_class_list_df.unique() #Numpy array
unique_class_list_df = unique_class_list_df.drop_duplicates()#Pandas df

# Record the number of unique classes in the data set
num_unique_classes = len(unique_class_list_df)

# Record the value for K, the number of clusters
K = num_unique_classes

# Remove the Instance and the Actual Class Column to create an unlabled
# data set
instance_id_colname = pd_data_set.columns[0]
class_column_colname = pd_data_set.columns[actual_class_column]
pd_data_set = pd_data_set.drop(columns = [ # Each row is a different instance
        instance_id_colname, class_column_colname]) 

# Convert dataframe into a Numpy array
np_data_set = pd_data_set.to_numpy(copy=True)

# Randomly select k instances from the data set. 
# These will be the cluster centroids for the first iteration
# of the algorithm.
centroids = np_data_set[np.random.choice(np_data_set.shape[
    0], size=K, replace=False), :]


##################### Cluster Assignment Step ################################
# Go through each instance and assign that instance to the closest 
# centroid (based on Euclidean distance).

# Initialize an array which will contain the cluster assignments for each
# instance.
cluster_assignments = np.empty(no_of_instances)

# Goes True if new centroids are the same as the old centroids
centroids_the_same = False

# Sets the maximum number of iterations
max_iterations = 300

while max_iterations > 0 and not(centroids_the_same):
    # Go through each data point and assign it to the nearest centroid
    for row in range(0, no_of_instances):
    
        this_instance = np_data_set[row]

        # Calculate the Euclidean distance of each instance in the data set
        # from each of the centroids
        # Find the centroid with the minimum distance and assign the instance
        # to that centroid.
        # Record that centroid in the cluster assignments array.
    
        # Reset the minimum distance to infinity
        min_distance = float("inf")

        for row_centroid in range(0, K):
            this_centroid = centroids[row_centroid]
        
            # Calculate the Euclidean distance from this instance to the
            # centroid
            distance = np.linalg.norm(this_instance - this_centroid)

            # If we have a centroid that is closer to this instance,
            # update the cluster assignment for this instance.
            if distance < min_distance:
                cluster_assignments[row] = row_centroid
                min_distance = distance # Update the minimum distance

    # Print after each cluster assignment has completed
    print("Cluster assignments completed for all " + str(
        no_of_instances) + " instances. Here they are:")
    print(cluster_assignments)
    print()
    print("Now calculating the new centroids...")
    print()

    outfile3.write("Cluster assignments completed for all " + str(
        no_of_instances) + " instances. Here they are:"+ "\n")
    outfile3.write(str(cluster_assignments))
    outfile3.write("\n")
    outfile3.write("\n")
    outfile3.write("Now calculating the new centroids..." + "\n")
    outfile3.write("\n")


    ##################### Move Centroid Step ################################
    # Calculate the centroids of the clusters by computing the average
    # of the attribute values of the instances in each cluster
    # For each row in the centroids 2D array

    # Store the old centroids
    old_centroids = centroids.copy()

    for row_centroid in range(0, K):

        # For each column of each row of the centroids 2D array
        for col_centroid in range(0, no_of_attributes):

            # Reset the running sum and the counter
            running_sum = 0.0
            count = 0.0
            average = None

            for row in range(0, no_of_instances):

                # If this instance belongs to this cluster
                if(row_centroid == cluster_assignments[row]):
                
                    # Add this value to the running sum
                    running_sum += np_data_set[row,col_centroid]

                    # Increment the counter
                    count += 1
        
                    if (count > 0):
                        # Calculate the average
                        average = running_sum / count

            # Update the centroids array with this average
            centroids[row_centroid,col_centroid] = average
    
    # Print to after each cluster assignment has completed
    print("New centroids have been created. Here they are:")
    print(centroids)
    print()

    outfile3.write("New centroids have been created. Here they are:" + "\n")
    outfile3.write(str(centroids))
    outfile3.write("\n")
    outfile3.write("\n")

    # Check if cluster centroids are the same
    centroids_the_same = np.array_equal(old_centroids,centroids)

    if centroids_the_same:
        print(
        "Cluster membership is unchanged. Stopping criteria has been met.")
        outfile3.write("Cluster membership is unchanged. ")
        outfile3.write("Stopping criteria has been met." + "\n")
        outfile3.write("\n")

    # Update the number of iterations
    max_iterations -= 1

# Record the actual class column name
actual_class_col_name = pd_full_data_set.columns[len(
    pd_full_data_set.columns) - 1]

# Add 4 additional columns to the original data frame
pd_full_data_set = pd_full_data_set.reindex(
      columns=[*pd_full_data_set.columns.tolist(
      ), 'Cluster', 'Silhouette Coefficient', 'Predicted Class', (
      'Prediction Correct?')])

# Add the final cluster assignments to the Pandas dataframe
pd_full_data_set['Cluster'] = cluster_assignments

outfile3.write("Calculating the Silhouette Coefficients. Please wait..." + "\n")
outfile3.write("\n")
print()
print("Calculating the Silhouette Coefficients. Please wait...")
print()
################## Calculate the Silhouette Coefficients ######################
# Rewards clusterings that have good cohesion and good separation. Varies 
# between 1 and -1. -1 means bad clustering, 1 means great clustering.

# 1. For each instance calculate the average distance to all other instances 
# in that cluster. This is a.
# 2. (Find the average distance to all the instances in the nearest neighbor 
# cluster). For each instance and any cluster that does not contain the 
# instance calculate the average distance to all
# of the points in that other cluster. Then return the minimum such value
# over all of the clusters. This is b.
# 3. For each instance calculate the Silhouette Coefficient s where
# s = (b-a)/max(a,b)
# Store the value in the data frame

silhouette_column = actual_class_column + 2

# Go through one instance at a time
for row in range(0, no_of_instances):

    this_instance = np_data_set[row]
    this_cluster = cluster_assignments[row]

    a = None
    running_sum = 0.0
    counter = 0.0

    # Calculate the average distance to all other instances 
    # in this cluster. This is a.
    # Go through one instance at a time
    for row_2 in range(0, no_of_instances):

        # If the other instance is in the same cluster as this instance
        if this_cluster == cluster_assignments[row_2]:

            # Calculate the distance
            distance = np.linalg.norm(this_instance - np_data_set[row_2])

            # Add the distance to the running sum
            running_sum += distance
            counter += 1

    # Calculate the value for a
    if counter > 0:
        a = running_sum / counter

    # For each instance and any cluster that does not contain the 
    # instance calculate the average distance to all
    # of the points in that other cluster. Then return the minimum such value
    # over all of the clusters. This is b.
    b = float("inf") 
    
    for clstr in range(0, K):

        running_sum = 0.0
        counter = 0.0

        # Must be other clusters, not the one this instance is in
        if clstr != this_cluster:

            # Calculate the average distance to instances in that 
            # other cluster
            for row_3 in range(0, no_of_instances):

                if cluster_assignments[row_3] == clstr:

                    # Calculate the distance
                    distance = np.linalg.norm(this_instance - np_data_set[
                        row_3])

                    # Add the distance to the running sum
                    running_sum += distance
                    counter += 1
        
            if counter > 0:
                avg_distance_to_cluster = running_sum / counter
        
            # Update b if we have a new minimum
            if avg_distance_to_cluster < b:
                b = avg_distance_to_cluster

    # Calculate the Silhouette Coefficient s where s = (b-a)/max(a,b)
    s = (b - a) / max(a,b)

    # Store the Silhouette Coefficient in the Pandas data frame
    pd_full_data_set.iloc[row,silhouette_column] = s

#################### Predict the Class #######################################
# For each cluster, determine the predominant class and assign that 
# class to the cluster. Then determine if the prediction was correct.
# Create a data frame that maps clusters to actual classes
class_mappings = pd.DataFrame(index=range(K),columns=range(1))

for clstr in range(0, K):

    # Select rows whose column equals that cluster value
    temp_df = pd_full_data_set.loc[pd_full_data_set['Cluster'] == clstr]
    
    # Select the predominant class
    class_mappings.iloc[clstr,0] = temp_df.mode()[actual_class_col_name][0]

cluster_column = actual_class_column + 1
pred_class_column = actual_class_column + 3
pred_correct_column = actual_class_column + 4

# Assign the relevant class to each instance
# See if prediction was correct
for row in range(0, no_of_instances):

    # Go through each of the clusters to check if the instance is a member
    # of that cluster
    for clstr in range(0, K):
        if clstr == pd_full_data_set.iloc[row,cluster_column]:

            # Assign the relevant class to this instance
            pd_full_data_set.iloc[
                row,pred_class_column] = class_mappings.iloc[clstr,0]

    # If the prediction was correct
    if pd_full_data_set.iloc[row,pred_class_column] == pd_full_data_set.iloc[
        row,actual_class_column]:
        pd_full_data_set.iloc[row,pred_correct_column] = 1
    else: # If incorrect prediction
        pd_full_data_set.iloc[row,pred_correct_column] = 0

# Write dataframe to a file
pd_full_data_set.to_csv(TEST_OUT_FILE, sep=",", header=True)

# Print data frame to the console
print()
print()
print("Data Set")
print(pd_full_data_set)
print()
print()

################### Summary Statistics #######################################
# Calculate the average Silhouette Coefficient for the data set
# Calculate the accuracy of the clustering-based classifier

# Open a new file to save the summary statistics
outfile1 = open(TEST_STATS_FILE,"w") 

# Write to a file
outfile1.write("----------------------------------------------------------\n")
outfile1.write(ALGORITHM_NAME + " Summary Statistics (Testing)\n")
outfile1.write("----------------------------------------------------------\n")
outfile1.write("Data Set : " + DATA_PATH + "\n")

# Write the relevant stats to a file
outfile1.write("\n")
outfile1.write("Number of Instances : " + str(no_of_instances) + "\n")
outfile1.write("\n")
outfile1.write("Value for k : " + str(K) + "\n")

# Calculate average Silhouette Coefficient for the data set
silhouette_coefficient = pd_full_data_set.loc[
    :,"Silhouette Coefficient"].mean()

# Write the Silhouette Coefficient to the file
outfile1.write("Silhouette Coefficient : " + str(
    silhouette_coefficient) + "\n")
      
# accuracy = (total correct predictions)/(total number of predictions)
accuracy = (pd_full_data_set.iloc[
        :,pred_correct_column].sum())/no_of_instances

accuracy *= 100

# Write accuracy to the file
outfile1.write("Accuracy : " + str(accuracy) + "%\n")

# Print statistics to console
print()
print()
print("-------------------------------------------------------")
print(ALGORITHM_NAME + " Summary Statistics (Testing)")
print("-------------------------------------------------------")
print("Data Set : " + DATA_PATH)

# Print the relevant stats to the console
print()
print("Number of Instances : " + str(no_of_instances))
print("Value for k : " + str(K))

# Print the Silhouette Coefficient to the console
print("Silhouette Coefficient : " + str(
    silhouette_coefficient))

# Print accuracy to the console
print("Accuracy : " + str(accuracy) + "%")

# Close the files
outfile1.close()
outfile3.close()

Return to Table of Contents

Output Statistics of K-means Clustering on the Iris Data Set

This section shows the results for the runs of K-means Clustering on the iris data set.

Test Statistics

Trace Runs

Here are the trace runs of the algorithm.

Output

Here is the output of the algorithm.

Return to Table of Contents

Stepwise Forward Selection Algorithm From Scratch

In this post, I will walk you through the Stepwise Forward Selection algorithm, step-by-step. We will develop the code for the algorithm from scratch using Python and use it for feature selection for the Naive Bayes algorithm we previously developed. We will then run the algorithm on a real-world data set, the iris data set (flower classification) from the UCI Machine Learning Repository. Without further ado, let’s get started!

What is the Stepwise Forward Selection Algorithm?
Stepwise Forward Selection Implementation
Stepwise Forward Selection Algorithm in Python, Coded From Scratch
Output Statistics of Stepwise Forward Selection on the Iris Data Set

What is the Stepwise Forward Selection Algorithm?

One of the fundamental ideas in machine learning is the Curse of Dimensionality – as the number of attributes in the training set grows, you need exponentially more instances to learn the underlying concept. And the more instances you have, the more computational time is required to process the data.

In other words, adding attributes improves performance, to a point. Beyond that point, you need to have exponentially more instances in order for performance to improve. This phenomenon is commonly known as the Hughes Effect (or Hughes Phenomenon).

Image Source: Hughes, G. (1968). On the Mean Accuracy Of Statistical Pattern Recognizers. IEEE Transactions on Information Theory, 14(1), 55-63.

In the above image, n = number of attributes and m = number of instances.

One technique for combatting the Curse of Dimensionality is known as Stepwise Forward Selection (SFS). SFS involves selecting only the most relevant attributes for learning and discarding the rest. The metric that determines what attribute is “most relevant” is determined by the programmer. In this project, I will use the classification accuracy of Naïve Bayes.

Because SFS is just a method to create an optimal attribute subset, it needs to be wrapped with another algorithm (in this case Naïve Bayes) that does the actual learning. For this reason, SFS is known as a wrapper method.

The goal of SFS is to reduce the number of features that a machine learning algorithm needs to examine by eliminating unnecessary features and finding an optimal attribute subset.

Suppose we have attributes A₁ through A_k which are used to describe a data set D.

A = <A₁,…A_k>

SFS begins with an empty attribute set:

A₀ = <>

It then selects an attribute from A, one at a time, until the performance (e.g. as measured by classification accuracy) of the target learning algorithm (e.g. Naïve Bayes) on a subset of the training data fails to improve performance.

Return to Table of Contents

Stepwise Forward Selection Implementation

Columns (0 through N)

0: Instance ID
1: Attribute 1
2: Attribute 2
3: Attribute 3
…
N: Actual Class

The program I developed (code is below) then adds 2 additional columns for the testing set.

N + 1: Predicted Class
N + 2: Prediction Correct? (1 if yes, 0 if no)

Here is what your data set should look like:

The iris data set contains 3 classes of 50 instances each (150 instances in total), where each class refers to a different type of iris flower. There are 4 attributes in the data set. Here is what an iris flower looks like in case you are interested:

=IF(B2>AVERAGE(B$2:B$151),1,0)

Here is how the data looks after the binarization:

Save the file as a csv file (comma-delimited), and load it into the program below (Python).

Here is a link to the final data set I used.

Return to Table of Contents

Stepwise Forward Selection Algorithm in Python, Coded From Scratch

Naïve Bayes was wrapped with SFS for feature selection. Classification accuracy was used to select the optimal attribute at each step. Once the optimal attribute subset was obtained, Naïve Bayes was run on the complete training set (67% of instances) and testing set (33% of instances), and classification accuracy was calculated.

Here is the code. Just copy and paste it into your favorite IDE. Don’t be scared at how long the code is. I use a lot of comments so that you know what is going on at each step:

import pandas as pd # Import Pandas library 
import numpy as np # Import Numpy library

# File name: sfs_naive_bayes.py
# Author: Addison Sears-Collins
# Date created: 6/10/2019
# Python version: 3.7
# Description: Implementation of Naive Bayes which uses Stepwise Forward 
# Selection (SFS) for feature selection. This code works for multi-class 
# classification problems (e.g. democrat/republican/independent)
# Calculate P(E1|CL0)P(E2|CL0)P(E3|CL0)...P(E#|CL0) * P(CL0) and
# P(E1|CL1)P(E2|CL1)P(E3|CL1)...P(E#|CL1) * P(CL1) and
# P(E1|CL2)P(E2|CL2)P(E3|CL2)...P(E#|CL2) * P(CL2), etc. and predict the
# class with the maximum result. 
# E is an attribute, and CL means class.
# Only need class prior probability and likelihoods to make a prediction
# (i.e. the numerator of Bayes formula) since denominators are same for both 
# the P(CL0|E1,E2,E3...)*P(CL0) and P(CL1|E1,E2,E3...)*P(CL1), etc. cases 
# where P means "probability of" and | means "given".

# Required Data Set Format:
# Columns (0 through N)
# 0: Instance ID
# 1: Attribute 1 
# 2: Attribute 2
# 3: Attribute 3 
# ...
# N: Actual Class 

# This program then adds 2 additional columns for the testing set.
# N + 1: Predicted Class
# N + 2: Prediction Correct? (1 if yes, 0 if no)

################ INPUT YOUR OWN VALUES IN THIS SECTION ######################
ALGORITHM_NAME = "SFS-Wrapped Naive Bayes"
DATA_PATH = "iris_dataset.txt"  # Directory where data set is located
TEST_STATS_FILE = "iris_dataset_naive_bayes_test_stats.txt"#Testing statistics
TEST_OUT_FILE = "iris_dataset_naive_bayes_test_out.txt" # Testing output
# Show functioning of the program
TRACE_RUNS_FILE  = "iris_dataset_naive_bayes_trace_runs.txt" 
SEPARATOR = ","  # Separator for the data set (e.g. "\t" for tab data)
TRAINING_DATA_PRCT = 0.67 # % of data set used for training. Default 0.67
testing_data_prct = 1 - TRAINING_DATA_PRCT # % of data set used for testing
SEED = 99  # SEED for the random number generator. Default: 99
#############################################################################

# Open a new file to save trace runs
outfile3 = open(TRACE_RUNS_FILE,"w") 

# Naive Bayes algorithm. Accepts a Pandas dataframeas its parameter
def naive_bayes(pd_data):
    # Create a training dataframe by sampling random instances from original data.
    # random_state guarantees that the pseudo-random number generator generates 
    # the same sequence of random numbers each time.
    pd_training_data = pd_data.sample(frac=TRAINING_DATA_PRCT, random_state=SEED)

    # Create a testing dataframe. Dropping the training data from the original
    # dataframe ensures training and testing dataframes have different instances
    pd_testing_data = pd_data.drop(pd_training_data.index)

    ######COMMENT OUT THESE TWO LINES BEFORE RUNNING ################
    #pd_training_data = pd_data.iloc[:20] # Used for testing only, gets 1st 20 rows
    #pd_testing_data = pd_data.iloc[20:22,:] # Used for testing only, rows 20 & 21

    # Calculate the number of instances, columns, and attributes in the
    # training data set. Assumes 1 column for the instance ID and 1 column
    # for the class. Record the index of the column that contains 
    # the actual class
    no_of_instances_train = len(pd_training_data.index) # number of rows
    no_of_columns_train = len(pd_training_data.columns) # number of columns
    no_of_attributes = no_of_columns_train - 2
    actual_class_column = no_of_columns_train - 1

    # Store class values in a column, sort them, then create a list of unique
    # classes and store in a dataframe and a Numpy array
    unique_class_list_df = pd_training_data.iloc[:,actual_class_column]
    unique_class_list_df = unique_class_list_df.sort_values()
    unique_class_list_np = unique_class_list_df.unique() #Numpy array
    unique_class_list_df = unique_class_list_df.drop_duplicates()#Pandas df

    # Record the number of unique classes in the data set
    num_unique_classes = len(unique_class_list_df)

    # Record the frequency counts of each class in a Numpy array
    freq_cnt_class = pd_training_data.iloc[:,actual_class_column].value_counts(
        sort=True)

    # Record the frequency percentages of each class in a Numpy array
    # This is a list of the class prior probabilities
    class_prior_probs = pd_training_data.iloc[:,actual_class_column].value_counts(
        normalize=True, sort=True)

    # Add 2 additional columns to the testing dataframe
    pd_testing_data = pd_testing_data.reindex(
                      columns=[*pd_testing_data.columns.tolist(
                      ), 'Predicted Class', 'Prediction Correct?'])

    # Calculate the number of instances and columns in the
    # testing data set. Record the index of the column that contains the 
    # predicted class and prediction correctness (1 if yes; 0 if no)
    no_of_instances_test = len(pd_testing_data.index) # number of rows
    no_of_columns_test = len(pd_testing_data.columns) # number of columns
    predicted_class_column = no_of_columns_test - 2
    prediction_correct_column = no_of_columns_test - 1

    ######################### Training Phase of the Model ########################
    # Create a an empty dictionary
    my_dict = {}

    # Calculate the likelihood tables for each attribute. If an attribute has
    # four levels, there are (# of unique classes x 4) different probabilities 
    # that need to be calculated for that attribute.
    # Start on the first attribute and make your way through all the attributes
    for col in range(1, no_of_attributes + 1):

        # Record the name of this column 
        colname = pd_training_data.columns[col]

        # Create a dataframe containing the unique values in the column
        unique_attribute_values_df = pd_training_data[colname].drop_duplicates()
        # Create a Numpy array containing the unique values in the column
        unique_attribute_values_np = pd_training_data[colname].unique()
    
        # Calculate likelihood of the attribute given each unique class value
        for class_index in range (0, num_unique_classes):
        
            # For each unique attribute value, calculate the likelihoods 
            # for each class
            for attr_val in range (0, unique_attribute_values_np.size) :
                running_sum = 0

                # Calculate N(unique attribute value && class value)
                # Where N means "number of" and && means "and"
                # Go through each row of the training set
                for row in range(0, no_of_instances_train):
                    if (pd_training_data.iloc[row,col] == (
                        unique_attribute_values_df.iloc[attr_val])) and (
                        pd_training_data.iloc[row, actual_class_column] == (
                        unique_class_list_df.iloc[class_index])):
                            running_sum += 1

                # With N(unique attribute value && class value) as the numerator
                # we now need to divide by the total number of times the class
                # appeared in the data set
                try:
                    denominator = freq_cnt_class[class_index]
                except:
                    denominator = 1.0
            
                likelihood = running_sum / denominator
            
                # Add a new likelihood to the dictionary
                # Format of search key is 
                # <attribute_name><attribute_value><class_value>
                search_key = str(colname) + str(unique_attribute_values_df.iloc[
                             attr_val]) + str(unique_class_list_df.iloc[
                             class_index])
                my_dict[search_key] = likelihood
 
    # Print the likelihood table to the console
    # print(pd.DataFrame.from_dict(my_dict, orient='index'))

    ################# End of Training Phase of the Naive Bayes Model ########

    ################# Testing Phase of the Naive Bayes Model ################

    # Proceed one instance at a time and calculate the prediction
    for row in range(0, no_of_instances_test):

        # Initialize the prediction outcome
        predicted_class = unique_class_list_df.iloc[0]
        max_numerator_of_bayes = 0.0

        # Calculate the Bayes equation numerator for each test instance
        # That is: P(E1|CL0)P(E2|CL0)P(E3|CL0)...P(E#|CL0) * P(CL0),
        # P(E1|CL1)P(E2|CL1)P(E3|CL1)...P(E#|CL1) * P(CL1)...
        for class_index in range (0, num_unique_classes):

            # Reset the running product with the class
            # prior probability, P(CL)
            try:
                running_product = class_prior_probs[class_index]
            except:
                running_product = 0.0000001 # Class not found in data set
        
            # Calculation of P(CL) * P(E1|CL) * P(E2|CL) * P(E3|CL)...
            # Format of search key is 
            # <attribute_name><attribute_value><class_value>
            # Record each search key value
            for col in range(1, no_of_attributes + 1):
                attribute_name = pd_testing_data.columns[col]
                attribute_value = pd_testing_data.iloc[row,col]
                class_value = unique_class_list_df.iloc[class_index]

                # Set the search key
                key = str(attribute_name) + str(
                          attribute_value) + str(class_value)

                # Update the running product
                try:
                    running_product *= my_dict[key]
                except:
                    running_product *= 0

            # Record the prediction if we have a new max
            # Bayes numerator
            if running_product > max_numerator_of_bayes:
                max_numerator_of_bayes = running_product
                predicted_class = unique_class_list_df.iloc[
                             class_index] # New predicted class

        # Store the prediction in the dataframe
        pd_testing_data.iloc[row,predicted_class_column] = predicted_class
    
        # Store if the prediction was correct
        if predicted_class == pd_testing_data.iloc[row,actual_class_column]:
            pd_testing_data.iloc[row,prediction_correct_column] = 1
        else: 
            pd_testing_data.iloc[row,prediction_correct_column] = 0

    print("-------------------------------------------------------")
    print("Learned Model Predictions on Testing Data Set")
    print("-------------------------------------------------------")

    # Print the revamped dataframe
    print(pd_testing_data)

    # accuracy = (total correct predictions)/(total number of predictions)
    accuracy = (pd_testing_data.iloc[
        :,prediction_correct_column].sum())/no_of_instances_test
    # Return classification accuracy
    return accuracy
    ####################### End Testing Phase ######################################    

# Stepwise forward selection method accepts a Pandas dataframe as a parameter
# and then returns the optimal dataframe from that dataframe.
def sfs(pd_data):

    # Record the name of the column that contains the instance IDs and the class
    instance_id_colname = pd_data.columns[0]
    no_of_columns = len(pd_data.columns) # number of columns
    class_column_index = no_of_columns - 1
    class_column_colname = pd_data.columns[class_column_index]

    # Record the number of available attributes
    no_of_available_attributes = no_of_columns - 2

    # Create a dataframe containing the available attributes by removing
    # the Instance and the Class Column
    available_attributes_df = pd_data.drop(columns = [
        instance_id_colname, class_column_colname]) 

    # Create an empty optimal attribute dataframe containing only the
    # Instance and the Class Columns
    optimal_attributes_df = pd_data[[instance_id_colname,class_column_colname]]

    # Set the base performance to a really low number
    base_performance = -9999.0

    # Check whether adding a new attribute to the optimal attributes dataframe
    # improves performance
    # While there are still available attributes left
    while no_of_available_attributes > 0: 
        # Set the best performance to a low number
        best_performance = -9999.0

        # Initialize the best attribute variable to a placeholder
        best_attribute = "Placeholder"

        # For all attributes in the available attribute data frame
        for col in range(0, len(available_attributes_df.columns)):

            # Record the name of this attribute
            this_attr = available_attributes_df.columns[col]
        
            # Create a new dataframe with this attribute inserted
            temp_opt_attr_df = optimal_attributes_df.copy()
            temp_opt_attr_df.insert(
                loc=1,column=this_attr,value=(available_attributes_df[this_attr]))

            # Run Naive Bayes on this new dataframe and return the 
            # classification accuracy
            current_performance = naive_bayes(temp_opt_attr_df)

            # Find the new attribute that yielded the greatest
            # classification accuracy
            if current_performance > best_performance:
                best_performance = current_performance
                best_attribute = this_attr

        # Did adding another feature lead to improvement?
        if best_performance > base_performance:
            base_performance = best_performance

            # Add the best attribute to the optimal attribute data frame
            optimal_attributes_df.insert(
                loc=1,column=best_attribute,value=(
                available_attributes_df[best_attribute]))

            # Remove the best attribute from the available attribute data frame
            available_attributes_df = available_attributes_df.drop(
                columns = [best_attribute]) 

            # Print the best attribute to the console
            print()
            print(str(best_attribute) + " added to the optimal attribute subset")
            print()

            # Write to file
            outfile3.write(str(
                best_attribute) + (
                " added to the optimal attribute subset") + "\n")
           
            # Decrement the number of available attributes by 1
            no_of_available_attributes -= 1

            # Print number of attributes remaining to the console
            print()
            print(str(no_of_available_attributes) + " attributes remaining")
            print()
            print()

            # Write to file
            outfile3.write(str(no_of_available_attributes) + (
                " attributes remaining") + "\n" + "\n")
           
        else:
            print()
            print("Performance did not improve this round.")
            print("End of Stepwise Forward Selection.")
            print()
            outfile3.write("Performance did not improve this round." + "\n")
            outfile3.write("End of Stepwise Forward Selection." + "\n")
            break

    # Return the optimal attribute set
    return optimal_attributes_df


def main():
    # Read the full text file and store records in a Pandas dataframe
    pd_full_data_set = pd.read_csv(DATA_PATH, sep=SEPARATOR)

    # Used for feature selection of large data sets only
    #pd_full_data_set = pd_full_data_set.sample(frac=0.10, random_state=SEED)
    
    # Runs SFS on the full data set to find the optimal attribute data frame
    optimal_attribute_set = sfs(pd_full_data_set)

    # Write dataframe to a file
    optimal_attribute_set.to_csv(TEST_OUT_FILE, sep=",", header=True)

    # Open a new file to save the summary statistics
    outfile2 = open(TEST_STATS_FILE,"w") 

    # Write to a file
    outfile2.write("----------------------------------------------------------\n")
    outfile2.write(ALGORITHM_NAME + " Summary Statistics (Testing)\n")
    outfile2.write("----------------------------------------------------------\n")
    outfile2.write("Data Set : " + DATA_PATH + "\n")

    # Write the relevant stats to a file
    outfile2.write("\n")
    outfile2.write("Number of Test Instances : " + 
        str(round(len(optimal_attribute_set.index) * testing_data_prct)) + "\n")
       
    # Run Naive Bayes on the optimal attribute set
    accuracy = naive_bayes(optimal_attribute_set)
    accuracy *= 100

    # Write accuracy to the file
    outfile2.write("Accuracy : " + str(accuracy) + "%\n")

    # Print statistics to console
    print()
    print()
    print("-------------------------------------------------------")
    print(ALGORITHM_NAME + " Summary Statistics (Testing)")
    print("-------------------------------------------------------")
    print("Data Set : " + DATA_PATH)

    # Print the relevant stats to the console
    print()
    print("Number of Test Instances : " + 
        str(round(len(optimal_attribute_set.index) * testing_data_prct)))

    # Print accuracy to the console
    print()
    print("Accuracy : " + str(accuracy) + "%")
    print()

    # Create a dataframe containing the optimal attributes by removing
    # the Instance and the Class Column
    instance_id_colname = optimal_attribute_set.columns[0]
    no_of_columns = len(optimal_attribute_set.columns) # number of columns
    class_column_index = no_of_columns - 1
    class_column_colname = optimal_attribute_set.columns[class_column_index]
    optimal_attribute_set = optimal_attribute_set.drop(columns = [
        instance_id_colname, class_column_colname]) 

    # Write a list of the optimal attribute set to a file
    outfile2.write("Optimal Attribute Subset : " + str(list(
        optimal_attribute_set)))

    # Print a list of the optimal attribute set
    print("Optimal Attribute Subset : " + str(list(optimal_attribute_set)))
    print()
    print()   
    
    # Close the files
    outfile2.close()
    outfile3.close()

main() # Call the main function

Return to Table of Contents