Now that we know how to derive displacement vectors for different types of robotic arms, let’s take a look at how to write displacement vectors in code.
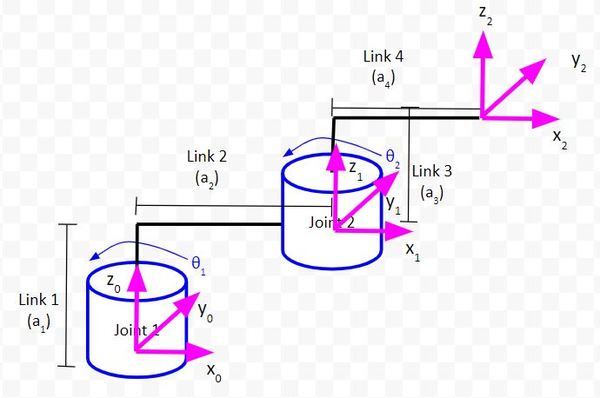
Two Degree of Freedom Robotic Arm
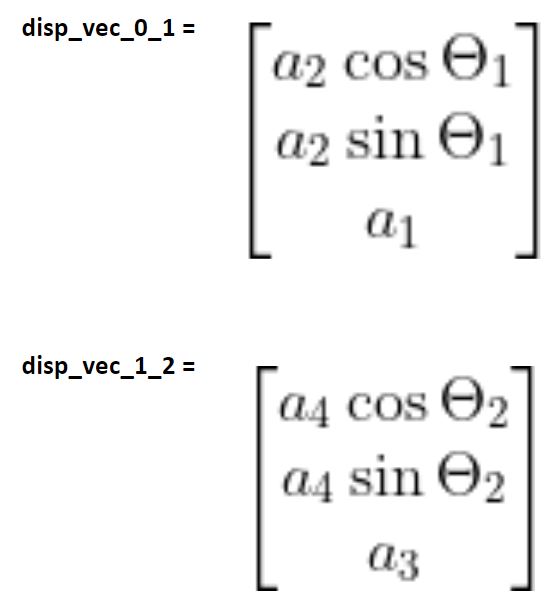
Here are the two displacement vectors we found earlier:
We’ve already found the rotation matrices for the two degrees of freedom robotic arm in a previous tutorial. I’ll start by copying and pasting that code into the program.
I will then write out the two displacement vectors.
Make sure that:
- servo_0_angle = 15 # Joint 1 (Theta 1)
- servo_1_angle = 60 # Joint 2 (Theta 2)
Here is the full code:
import numpy as np # Scientific computing library
# Project: Displacement Vectors for a 2 DOF Robotic Arm
# Author: Addison Sears-Collins
# Date created: August 10, 2020
# Servo (joint) angles in degrees
servo_0_angle = 15 # Joint 1 (Theta 1)
servo_1_angle = 60 # Joint 2 (Theta 2)
# Link lengths in centimeters
a1 = 1 # Length of link 1
a2 = 1 # Length of link 2
a3 = 1 # Length of link 3
a4 = 1 # Length of link 4
# Convert servo angles from degrees to radians
servo_0_angle = np.deg2rad(servo_0_angle)
servo_1_angle = np.deg2rad(servo_1_angle)
# Define the first rotation matrix.
# This matrix helps convert servo_1 frame to the servo_0 frame.
# There is only rotation around the z axis of servo_0.
rot_mat_0_1 = np.array([[np.cos(servo_0_angle), -np.sin(servo_0_angle), 0],
[np.sin(servo_0_angle), np.cos(servo_0_angle), 0],
[0, 0, 1]])
# Define the second rotation matrix.
# This matrix helps convert the
# end-effector frame to the servo_1 frame.
# There is only rotation around the z axis of servo_1.
rot_mat_1_2 = np.array([[np.cos(servo_1_angle), -np.sin(servo_1_angle), 0],
[np.sin(servo_1_angle), np.cos(servo_1_angle), 0],
[0, 0, 1]])
# Calculate the rotation matrix that converts the
# end-effector frame to the servo_0 frame.
rot_mat_0_2 = rot_mat_0_1 @ rot_mat_1_2
# Display the rotation matrix
print(rot_mat_0_2)
# Displacement vector from frame 0 to frame 1. This vector describes
# how frame 1 is displaced relative to frame 0.
disp_vec_0_1 = np.array([[a2 * np.cos(servo_0_angle)],
[a2 * np.sin(servo_0_angle)],
[a1]])
# Displacement vector from frame 1 to frame 2. This vector describes
# how frame 2 is displaced relative to frame 1.
disp_vec_1_2 = np.array([[a4 * np.cos(servo_1_angle)],
[a4 * np.sin(servo_1_angle)],
[a3]])
# Display the displacement vectors
print() # Add a space
print(disp_vec_0_1)
print() # Add a space
print(disp_vec_1_2)
Now run the code. Here is the output for both the rotation matrix and the displacement vectors:
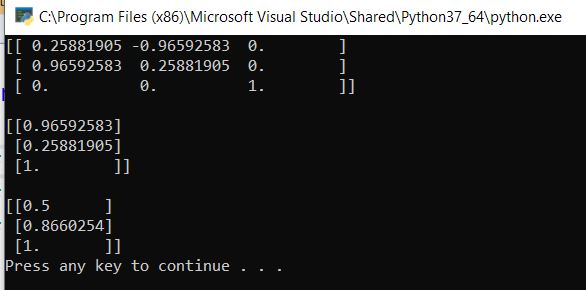
References
Credit to Professor Angela Sodemann from whom I learned these important robotics fundamentals. Dr. Sodemann teaches robotics over at her website, RoboGrok.com. While she uses the PSoC in her work, I use Arduino and Raspberry Pi since I’m more comfortable with these computing platforms. Angela is an excellent teacher and does a fantastic job explaining various robotics topics over on her YouTube channel.

