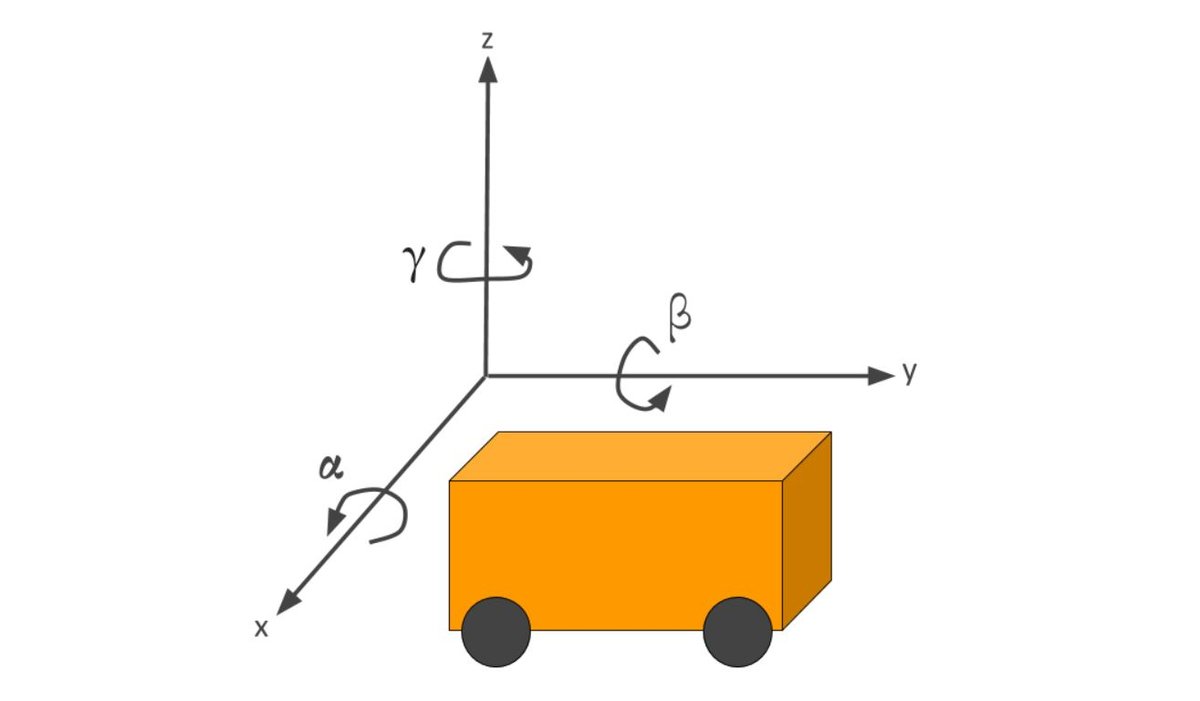
Given a quaternion of the form  (x, y, z, w) where w is the scalar (real) part and x, y, and z are the vector parts, how do we convert this quaternion into the three Euler angles:

• Rotation about the x axis = roll angle = α
• Rotation about the y-axis = pitch angle = β
• Rotation about the z-axis = yaw angle = γ

Doing this operation is important because ROS2 (and ROS) uses quaternions as the default representation for the orientation of a robot in 3D space. Roll, pitch, and yaw angles are a lot easier to understand and visualize than quaternions.

Here is the Python code:

import math

def euler_from_quaternion(x, y, z, w):
		"""
		Convert a quaternion into euler angles (roll, pitch, yaw)
		roll is rotation around x in radians (counterclockwise)
		pitch is rotation around y in radians (counterclockwise)
		yaw is rotation around z in radians (counterclockwise)
		"""
		t0 = +2.0 * (w * x + y * z)
		t1 = +1.0 - 2.0 * (x * x + y * y)
		roll_x = math.atan2(t0, t1)
    
		t2 = +2.0 * (w * y - z * x)
		t2 = +1.0 if t2 > +1.0 else t2
		t2 = -1.0 if t2 < -1.0 else t2
		pitch_y = math.asin(t2)
    
		t3 = +2.0 * (w * z + x * y)
		t4 = +1.0 - 2.0 * (y * y + z * z)
		yaw_z = math.atan2(t3, t4)
    
		return roll_x, pitch_y, yaw_z # in radians

Example

Suppose a robot is on a flat surface. It has the following quaternion:

Quaternion [x,y,z,w] = [0, 0, 0.7072, 0.7072]

What is the robot’s orientation in Euler Angle representation in radians?

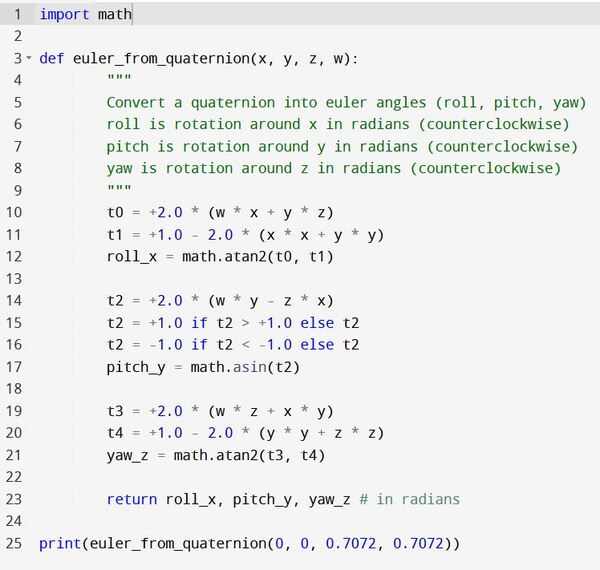
The program shows that the roll, pitch, and yaw angles in radians are (0.0, 0.0, 1.5710599372799763).

Which is the same as:

Euler Angle (roll, pitch, yaw) = (0.0, 0.0, π/2)

And in Axis-Angle Representation, the angle is:

Axis-Angle {[x, y, z], angle} = { [ 0, 0, 1 ], 1.571 }

So we see that the robot is rotated π/2 radians (90 degrees) around the z axis (going counterclockwise). 

And that’s all there is to it folks. That’s how you convert a quaternion into Euler angles.

You can use the code in this tutorial for your work in ROS2 since, as of this writing, the tf.transformations.euler_from_quaternion method isn’t available for ROS2 yet.