Let’s examine what reinforcement learning is all about by looking at an example.

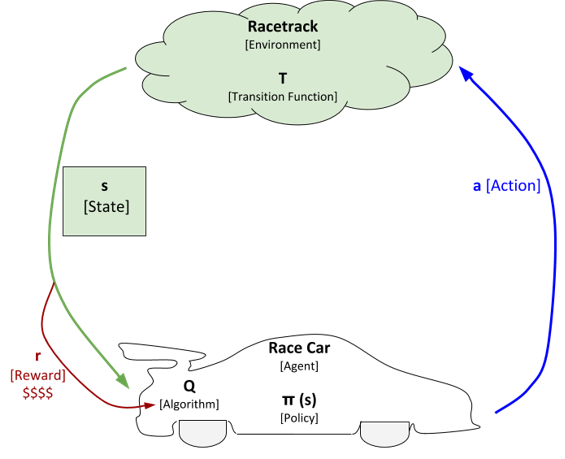
We have a race car that drives all by itself (i.e. autonomous race car). The race car will move around in an environment. Formally, the race car is known in reinforcement learning language as the agent. The agent is the entity in a reinforcement learning problem that is learning and making decisions. An agent in this example is a race car, but in other applications it could be a robot, self-driving car, autonomous helicopter, etc.

The race car will interact with the environment. The environment in this example is the racetrack. It is represented as the little cloud in the image above. Formally, the environment is the world in which the agent learns and makes decisions. In this example, it is a race track, but in other applications it could be a chessboard, bedroom, warehouse, stock market, factory, etc. 

In order to interact with the environment, the race car has to take actions (i.e. accelerate, decelerate, turn). Each time the race car takes an action it will change the environment. Formally, actions are the set of things that an agent can do. In a board game like chess, for example, the set of actions could be move-left, move-right, move-up, and move-down.

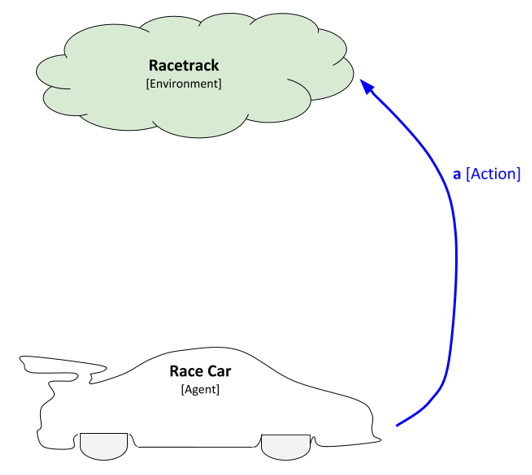
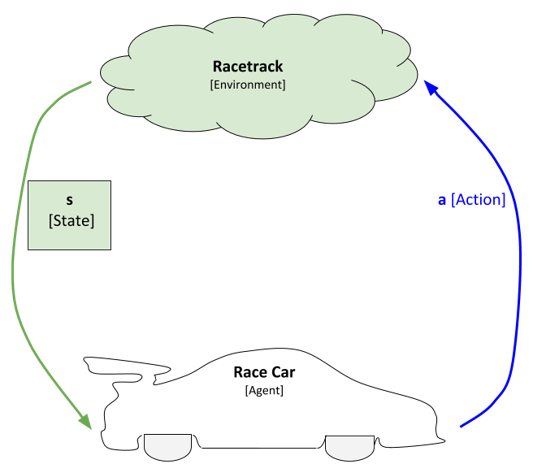
Each time the environment changes, the race car will sense the environment. In this example, sensing the environment means taking an observation of its current position on the racetrack and its velocity (i.e. speed). The position and velocity variables are what we call the current state of the environment. The state is what describes the current environment. In this example, position and velocity constitute the state, but in other applications the state could be any kind of observable value (i.e. roll, pitch, yaw, angle of rotation, force, etc.)

After the race car observes the new state, it has to process that state in order to decide what to do next. That decision-making process is called the policy of the agent. You can think of the policy as a function. It takes as inputs the observed state (denoted as s) and outputs an action (denoted as a). The policy is commonly represented as the Greek letter π. So, the function is formally π(s) = a.

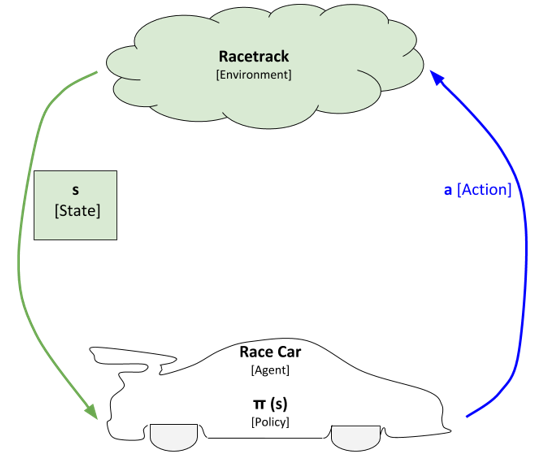
In robotics, the cycle I described above is often referred to as the sense-think-act cycle. 

Diving into even greater detail on how this learning cycle works…once the policy of the race car (i.e. the agent) outputs an action, the race car then takes that action. That action causes the environment to transition to a new state. That transition is often represented as the letter T (i.e. the transition function). The transition function takes as input the previous state and the new action. The output of the transition function is a new state.

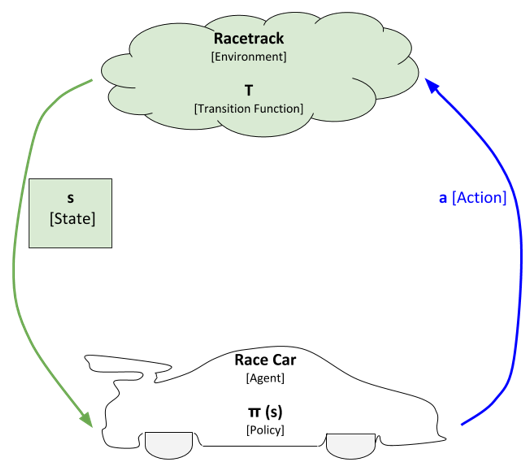
The robot then observes the new state, examines its policy, and executes a new action. This cycle repeats over and over again.

So the question now is, how is the policy π(s) determined? In other words, how does the race car know what action to take (i.e. accelerate, decelerate, turn) when it observes a particular state (i.e. position on the racetrack and velocity)?

In order to answer those questions, we need to add another piece to the diagram. That piece is known as the reward. The reward is what helps the race car develop a policy (i.e. a plan of what action to take in each state). Let us draw the reward piece on the diagram and then take a closer look at what this is.

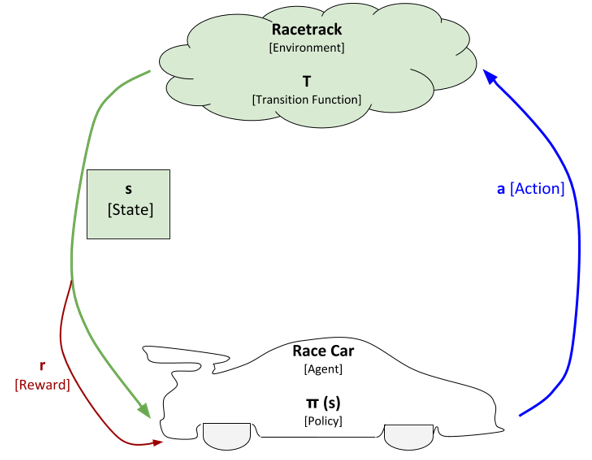
Every time the race car is in a particular state and takes an action, there is a reward that the race car receives from the environment for taking that action in that particular state. That reward can be either a positive reward or a negative reward. Consider the reward the feedback that the race car (i.e. agent) receives from the environment for taking an action. The reward tells the race car how well it is doing.

It is helpful to imagine that there is a pocket on the side of the race car that stores “money.” Every time the race car takes an action from a particular state, the environment either adds money to that pocket (positive reward) or removes money from that pocket (negative reward). 

The actual value for the reward (i.e. r in the diagram above) depends on what is known as the reward function. We can denote the reward function as R. The reward function takes as inputs a state, action, and new state and outputs the reward.

R[s, a, s’] —-> r

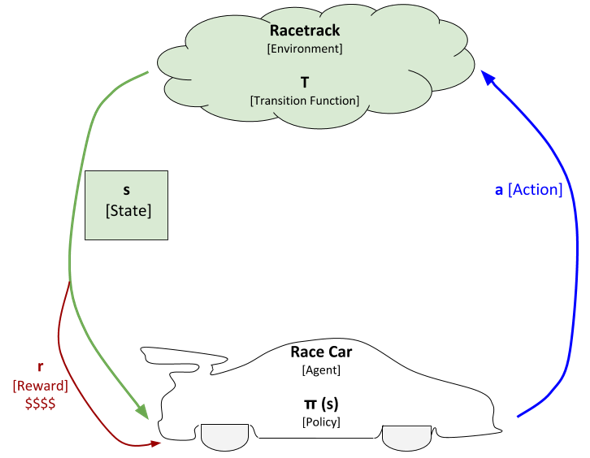
The reward is commonly an integer (e.g. +1 for a positive reward; -1 for a negative reward). In this project, the reward for each move is -1. The reason why the reward for each move is -1 is because we want to teach the race car to move from the starting position to the finish line in the minimum number of timesteps. By penalizing the race car each time it makes a move, we ensure that it gradually learns how to avoid penalties and finishes the race as quickly as possible.

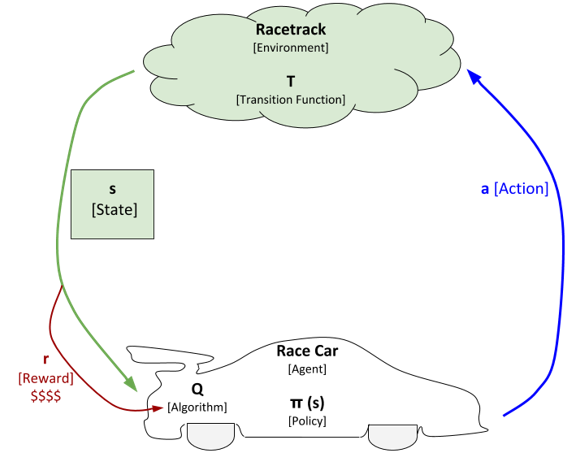
Inside the race car, there is an algorithm that keeps track of what the rewards were when it took an action in a particular state. This algorithm helps the race car improve over time. Improvement in this case means learning a policy that enables it to take actions (given a particular state) that maximize its total reward. 

We will represent this algorithm as Q, where Q is used by the race car in order to develop an optimal policy, a policy that enables the race car to maximize its total reward.

Reinforcement Learning Summary

Summarizing the steps in the previous section, on a high level reinforcement learning has the following steps:

1. The agent (i.e race car) takes an observation of the environment. This observation is known as the state.
2. Based on this state, the race car uses its policy to determine what action to take, where policy is typically a lookup table that matches states to particular actions.
3. Based on the state and the action taken by the agent, the environment transitions to a new state and generates a reward.
4. The reward is passed from the environment to the agent.
5. The agent keeps track of the rewards it receives for the actions it takes in the environment from a particular state. It uses the reward information to update its policy. The goal of the agent is to learn the best policy over time (i.e. where policy is typically a lookup table that tells the race car what action to take given a particular state). The best policy is the one that maximizes the total reward of the agent.

Markov Decision Problem

The description of reinforcement learning I outlined in the previous section is known as a Markov decision problem. A Markov decision problem has the following components:

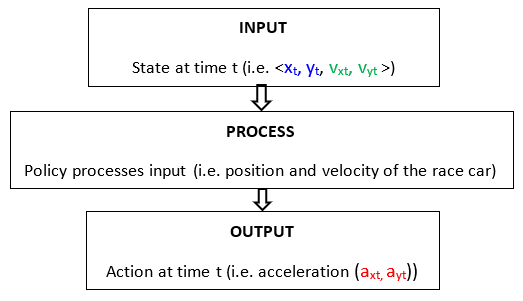
• Set of states S: All the different values of s that can be observed by the race car (e.g. position on the racetrack, velocity). In this project, the set of states is all the different values that <x_t, y_t, v_xt, v_yt> can be.
• Set of actions A: All the different values of a that are the actions performed by the race car on the environment (e.g. accelerate, decelerate, turn). In this project, the set of actions is all the different values that = <a_xt, a_yt> can be.
• Transition Function T[s, a, s’]
  • Where T[s, a, s’] stands for the probability the race car finds itself in a new state s’ (at the next timestep) given that it was in state s and took action a.
  • In probability notation, this is formally written as: 
    • T[s, a, s’] = P[new state = s’ | state = s AND action = a], where P means probability and | means “given” or “conditioned upon.”
• Reward Function R[s,a,s’]
  • Given a particular state s and a particular action a that changes to state from s to s’, the reward function determines what the reward will be (e.g. -1 reward for all portions of the racetrack except for the finish line, which has reward of 0).

The goal of a reinforcement learning algorithm is to find the policy (denoted as π(s)) that can tell the race car the best action to take in any particular state, where “best” in this context means the action that will maximize the total reward the race car receives from the environment. The end result is the best sequence of actions the race car can take to maximize its reward (thereby finishing the race in the minimum number of timesteps). The sequence of actions the race car takes from the starting position to the finish line is known denotes an episode or trial. (Alpaydin, 2014). Recall that the policy is typically a lookup table that matches states (input) to actions (output).

There are a number of algorithms that can be used to enable the race car to learn a policy that will enable it to achieve its goal of moving from the starting position of the racetrack to the finish line as quickly as possible. The two algorithms implemented in this project were value iteration and Q-learning. These algorithms will be discussed in detail in future posts.

Helpful Video

This video series by Dr. Tucker Balch, a professor at Georgia Tech, provides an excellent introduction to reinforcement learning.