The K-means clustering algorithm is used to group unlabeled data set instances into clusters based on similar attributes. It has a number of advantages over other types of machine learning models, including the linear models, such as logistic regression and Naive Bayes.

Here are the advantages:

Unlabeled Data Sets

A lot of real-world data comes unlabeled, without any particular class. The benefit of using an algorithm like K-means clustering is that we often do not know how instances in a data set should be grouped. 

For example, consider the problem of trying to group viewers of Netflix into clusters based on similar viewing behavior. We know that there are clusters, but we do not know what those clusters are. Linear models will not help us at all with these sorts of issues.

Nonlinearly Separable Data

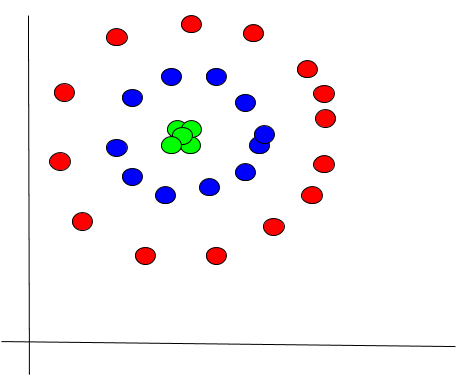
Consider the data set below containing a set of three concentric circles. It is nonlinearly separable. In other words, there is no straight line or plane that we could draw on the graph below that can easily discriminate the colored classes red, blue, and green. Using K-means clustering and converting the coordinate system below from Cartesian coordinates to Polar coordinates, we could use the information about the radius to create concentric clusters.

Simplicity

The meat of the K-means clustering algorithm is just two steps, the cluster assignment step and the move centroid step. If we’re looking for an unsupervised learning algorithm that is easy to implement and can handle large data sets, K-means clustering is a good starting point. 

Availability

Most of the popular machine learning packages contain an implementation of K-means clustering.

Speed

Based on my experience using K-means clustering, the algorithm does its work quickly, even for really big data sets.