How to Create a Launch File for C++ Nodes
Up until now, when we wanted to run a ros node, we:
- Opened a terminal window
- Typed roscore
- Opened another terminal window
- Typed rosrun <name_of_package> <name_of_node>
Running one or two nodes is fine this way. However, imagine if you had to run 30 nodes. You would have to open 30 separate terminal windows just to run each node!
Fortunately, there is a better way. ROS has a tool called the launch file that enables you to launch more than one node at the same time.
A launch file is in a special format called XML format. It is in this file that you will list the nodes that you would like the ROS system to launch simultaneously.
Let’s look at how to create a launch file in ROS that launches two nodes at the same time. We will launch simple_publisher_node and simple_subscriber_node that exist inside the noetic_basics_part_1 package.
First, open a new terminal window.
Go to your package folder.
roscd noetic_basics_part_1
Create a new folder named, launch.
mkdir launch
Move into that directory.
cd launch
Open a new file named noetic_basics_part_1.launch.
gedit noetic_basics_part_1.launch
Type the following code in the file, and then click Save.
<launch>
<node
pkg="noetic_basics_part_1"
type="simple_publisher_node"
name="simple_publisher_node"
output="screen"
/>
<node
pkg="noetic_basics_part_1"
type="simple_subscriber_node"
name="simple_subscriber_node"
output="screen"
/>
</launch>
Every launch file in ROS needs to have exactly one root element. All the other stuff in the launch file needs to be between these two tags.
<launch>
…
</launch>
Between the <launch> and </launch> tags, you list the nodes that you want to launch.
<node
pkg="name_of_the_package"
type="name_of_the_executable"
name="name_of_the_node"
/>
pkg and type let us know which program ROS needs to run. These two lines are equivalent to what you would type in the terminal window manually using the rosrun command.
For example, in this command:
rosrun noetic_basics_part_1 simple_publisher_node
pkg is the name of the package…in this case, noetic_basics_part_1.
type is the name of the executable file we want ROS to run…in this case, simple_publisher_node.
Remember you can see all your executables in the ~/catkin_ws/devel/lib/noetic_basics_part_1/ folder. These executables were created from your C++ programs (.cpp) when you typed the catkin_make command.
name assigns a name to the node. This name overrides that name that the node (i.e. C++ program we wrote earlier in this tutorial) would usually have due to the ros::init call. I kept the name as-is.
Finally, we have the output=”screen” element. This element tells ROS to display the output to the terminal window instead of inside special files called log files (which are inside the ~/.ros/log directory).
Now that we’ve created the launch file, let’s run it. The syntax for running a launch file is as follows:
roslaunch package-name launch-file-name
Open a new terminal window, and type:
roslaunch noetic_basics_part_1 noetic_basics_part_1.launch
Here is the output:
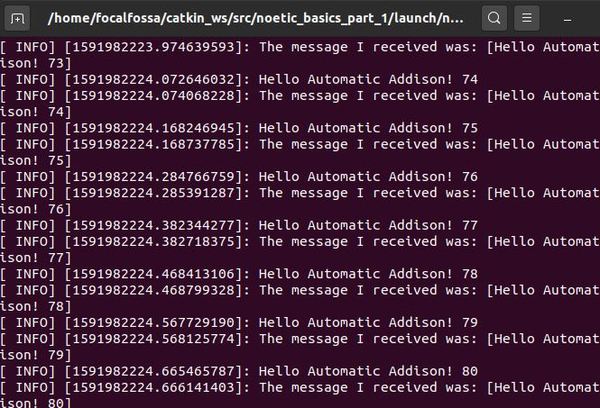
Press CTRL + C when you want the nodes to stop.
Notice that when you use roslaunch, you do not have to execute the roscore command. roslaunch starts up roscore automatically.
How to Create a Launch File for Python Nodes
First, open a new terminal window.
Go to your package launch folder.
roscd noetic_basics_part_1/launch
Open a new file named noetic_basics_part_1_py.launch.
gedit noetic_basics_part_1_py.launch
Type the following code in the file, and then click Save.
<launch>
<node
pkg="noetic_basics_part_1"
type="simple_python_publisher.py"
name="simple_python_publisher"
output="screen"
/>
<node
pkg="noetic_basics_part_1"
type="simple_python_subscriber.py"
name="simple_python_subscriber"
output="screen"
/>
</launch>
Open a new terminal window, and type:
roslaunch noetic_basics_part_1 noetic_basics_part_1_py.launch
Here is the output:
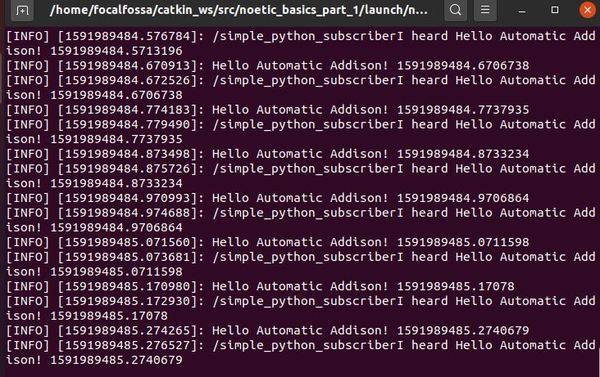
Press CTRL + C when you want the nodes to stop.