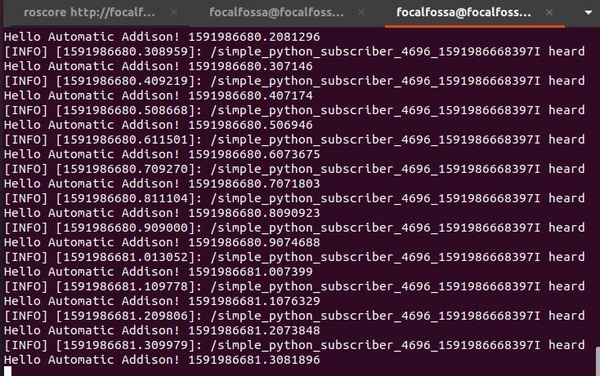
Up until now, we have worked with standard type messages (e.g. strings). Let’s see how we can create our own custom messages in ROS.
Open a new terminal window, and type the following command to go to the noetic_basics_part_1 package:
roscd noetic_basics_part_1
Create a msg folder inside that package.
mkdir msg
Move inside that folder.
cd msg
Create a new .msg file
gedit noetic_basics_part_1_msg.msg
Add the following lines.
int32 A
int32 B
int32 C

Click Save and close out the window.
In the code above, we have written three message descriptions. Specifically, we have declared three signed 32-bit integers. The syntax for a message description is:
fieldtype fieldname
Now, go back to the package.
roscd noetic_basics_part_1
Open the package.xml file.
gedit package.xml
Uncomment these two lines by deleting the arrows on each side:
<build_depend>message_generation</build_depend>
<exec_depend>message_runtime</exec_depend>
Click Save, and then close the editor.
Now open CMakeList.txt.
gedit CMakeList.txt
Add message_generation inside the find_package(catkin REQUIRED COMPONENTS…) scope.
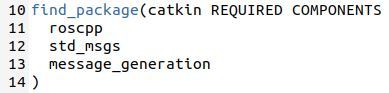
Also uncomment the add_message_files (…) lines and add the name of the message you just created.
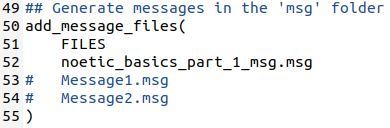
Now uncomment the generate_messages(…) lines.
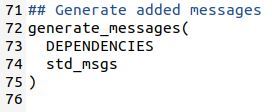
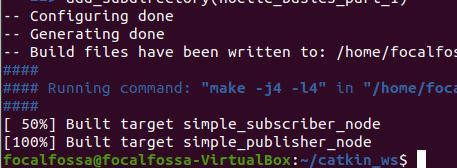
Since we made all these changes, we now need to build the package.
cd ~/catkin_ws/
catkin_make
Check to see if everything built properly by typing the following command:
rosmsg show noetic_basics_part_1/noetic_basics_part_1_msg
Here is what you should see:

You can also see the custom message you just created by typing this command:
rosmsg list
The message types are listed in alphabetic order by package name.
You can also just see a list of message types for just the noetic_basics_part_1 package.
rosmsg package noetic_basics_part_1